论文笔记 一种计算组织存在概率及相关关系的方法
论文笔记 NetworkTrace: Probabilistic Relevant Pattern Recognition Approach to Attribution Trace Analysis
本文提出了一种NetworkTrace框架用于分析网络攻击痕迹之间的归属关系,并提出了计算可疑组织存在的概率的一种方法。
NETWORKTRACE 框架的设计
该框架可以分为两个部分,上层的标识层以及下层的追踪层。每层都包含顶点和边,标识层顶点为inode,描述了诸如人员或组织之类,一个inode唯一标识一个组织或个人。追踪层顶点为itrace,标识诸如电子邮件,手机,ip位置等相关属性。
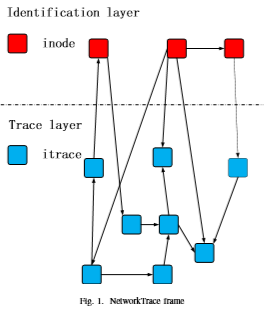
存在概率
如上图所示,一个inode节点存在的概率取决于不同itrace的可靠性以及所连接的inode。如果eij∈E,则vj与vi相邻。令EP(vi)表示vi∈V的存在概率,则通过以下公式可算出vi顶点存在的概率。
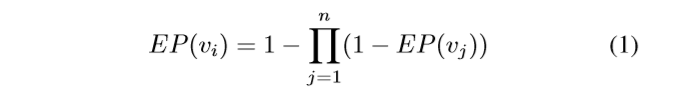
以上公式是针对无环时的情况,当节点之间的关系形成环时,itrace存在的概率将和他所在关系环的数量呈正相关,itrace存在概率有以下公式。其中n表示该顶点所在环数量,Xstep表示每个相关环的增量。EPinit表示v顶点初始存在可能性。
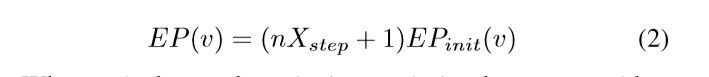
将公式1和公式2结合起来,得到以下顶点存在概率公式
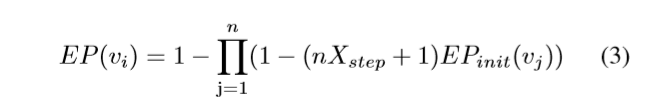
以上是存在概率的理论,接下来是该理论的实现方法。本文以广度优先搜索算法为基础。如下图

EP算如下,该算法利用BFS算法遍历连接到目标inode的所有顶点。 在BFS的每次迭代期间,它都采用公式3来确定发现的顶点的存在概率。

相关性
节点的连接方式有两种,直接连接和间接连接。
-
直接连接:如果∃inodei,inode j∈Videntis和∃eij∈E。这表明inode形成了牢固的关系。 例如,当反向分析组织(inodej)交付的恶意软件时,在作者字符串中会发现Bob的名字(inodei),这样就形成了直接连接。
-
间接连接:例如Bob使用的私人电子邮件,以及共享邮件等。
当Vi与Vj节点之间有多条连接路径时,其相关性计算公式如下,其中n是连接路径的数量。 k是每个连接路径中的边数。 r(Xij,X i(j+1))是每个顶点对的相关性。
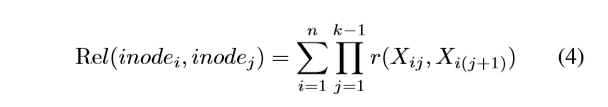
相关性算法实现如下


