以邻接矩阵为存储结构的图的基本操作

1代码

1.1创建图的邻阶矩阵

void CreateMGraph(MGraph &g, int n, int e)//建图 
{
	int  x,y;
	//初始化邻接矩阵	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			g.edges[i][j] = 0;
		}
	}

	for(int i=0;i<e;i++){
		cin>>x>>y;
		g.edges[x][y] = 1;		//对称矩阵
		g.edges[y][x] = 1;
    }
	g.n=n;
}

1.2以邻接矩阵为存储结构遍历算法

深度优先遍历

void DFS(MGraph g, int v)//深度遍历 
{
	static int n = 0;
	int j;
	if (!visited[v]) {
		if (!n) {
			cout << v;
			n++;
		}
		else
			cout << ' ' << v;
		visited[v] = 1;
	}
	for (j = 1; j <= g.n; j++) {
		if (!visited[j] && g.edges[v][j] == 1)
			DFS(g, j);
	}
}

广度优先遍历

void BFS(MGraph g, int v)//广度遍历 
{
	int i, j, x, n = 0;
	queue<int>q;
	if (!visited[v]) {
		cout << v;
		visited[v] = 1;
		q.push(v);
	}
	while (!q.empty()) {
		x = q.front();
		q.pop();
		for (j = 1; j <= g.n; j++) {
			if (g.edges[x][j] && !visited[j]) {
				cout << ' ' << j;
				visited[j] = 1;
				q.push(j);
			}
		}
	}
}

2完整代码

#define  MAXV  20
#include <stdio.h>
#include <stdlib.h>
#include<queue>
#include <iostream>
using namespace std;
//图的邻接矩阵	
typedef struct  			//图的定义
{
	int edges[MAXV][MAXV]; 	//邻接矩阵
	int n, e;  			//顶点数，弧数
} MGraph;				//图的邻接矩阵表示类型
int visited[100];
int flag = 0;
void DFS(MGraph g, int v);//深度遍历 
void BFS(MGraph g, int v);//广度遍历 
void CreateMGraph(MGraph &g, int n, int e);//建图 
int main()
{
	MGraph g;
	int n, e, i, v;
	cin >> n >> e;
	CreateMGraph(g, n, e);
	cin >> v;
	if (n >= 1 && n <= g.n)
	{
		for (i = 1; i <= g.n; i++) visited[i] = 0;
		cout << "dfs:";
		DFS(g, v);
		cout << endl;
		for (i = 1; i <= g.n; i++) visited[i] = 0;
		cout << "bfs:";
		BFS(g, v);
	}
	system("pause");
	return 0;
}

void CreateMGraph(MGraph &g, int n, int e)//建图 
{
	int  x,y;
	//初始化邻接矩阵	
	for (int i = 1; i <= n; i++) {
		for (int j = 1; j <= n; j++) {
			g.edges[i][j] = 0;
		}
	}

	for(int i=0;i<e;i++){
		cin>>x>>y;
		g.edges[x][y] = 1;		//对称矩阵
		g.edges[y][x] = 1;
    }
	g.n=n;
}


void DFS(MGraph g, int v)//深度遍历 
{
	static int n = 0;
	int j;
	if (!visited[v]) {
		if (!n) {
			cout << v;
			n++;
		}
		else
			cout << ' ' << v;
		visited[v] = 1;
	}
	for (j = 1; j <= g.n; j++) {
		if (!visited[j] && g.edges[v][j] == 1)
			DFS(g, j);
	}
}

void BFS(MGraph g, int v)//广度遍历 
{
	int i, j, x, n = 0;
	queue<int>q;
	if (!visited[v]) {
		cout << v;
		visited[v] = 1;
		q.push(v);
	}
	while (!q.empty()) {
		x = q.front();
		q.pop();
		for (j = 1; j <= g.n; j++) {
			if (g.edges[x][j] && !visited[j]) {
				cout << ' ' << j;
				visited[j] = 1;
				q.push(j);
			}
		}
	}
}

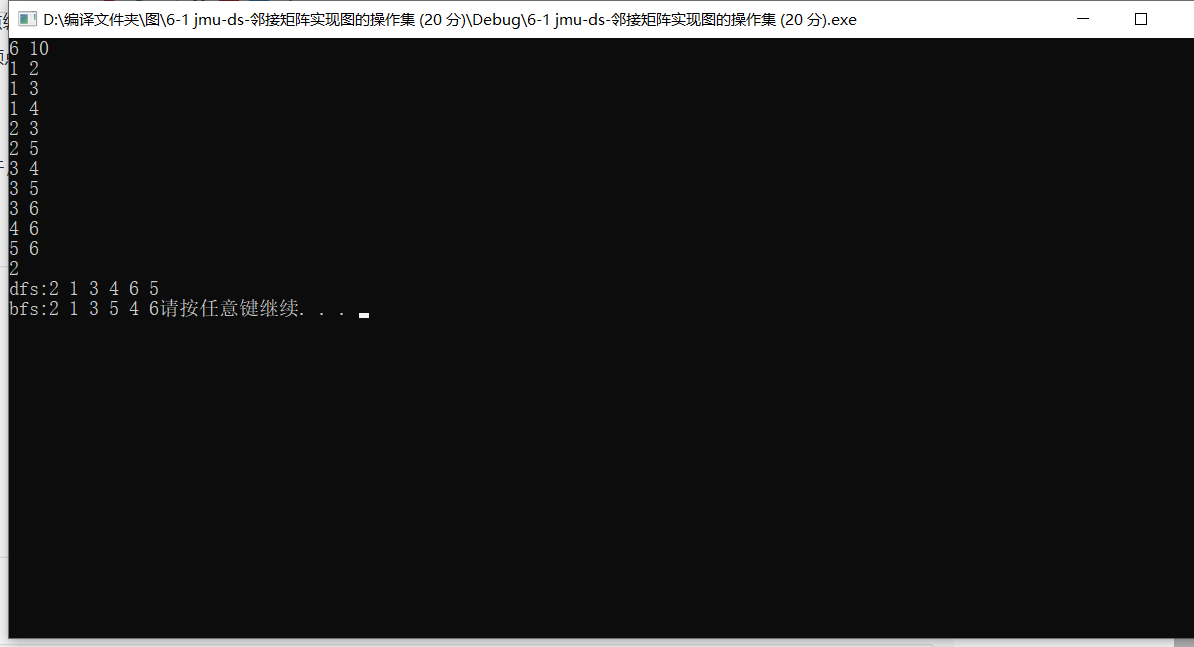
3运行结果