基于学习哈希的高效段落检索（Efficient Passage Retrieval with Hashing for Open-domain Question Answering）

Abstract

大多数SOTA的开放域问答系统都使用了神经检索模型，将段落编码成一个连续的向量，然后进行检索。但这种检索模型因为需要为存储的vector建立索引，每次运行都需要大量的内存。这篇论文提出了BPR(Binary Passage Retriever)，将learning-to-hash技术和DPR技术结合，将段落索引从连续向量表示为二进制的形式。
BPR通过一个多任务学习进行训练

• 通过二进制编码检索产生有效的候选段落
• 在连续向量上的重排训练
  和DPR相比，BPR能够将存储损耗从65GB减少到2GB，并且只造成了一点精度上的损失。

Introduction

Open-domain QA任务是从知识库中检索有关于任何事实问题的回答。
最近SOTA的任务都是建立在两阶段retriever-reader的方法上。其中retriever从大型的知识库中检索到少量的相关段落，reader从这些段落中获取到答案，比较出名的就是DPR模型。
这种使用独立编码器的模型比BM25检索效果更好，但是他们存在一个问题：由于段落索引的规模，系统在运行时需要很大的内存占用。

因此为了缓解这个问题，作者提出了BPR模型。BPR模型通过端到端的多任务学习方法，能够同时训练到编码器和哈希函数，最终能够将连续的向量hash成一个二进制编码。

为了在提升检索效率的同时保证检索精度，BPR模型在两个任务上训练以得到二进制代码以及问题的连续向量表示。

• 通过question的二进制编码和passage的二进制编码，利用汉明距离产生候选的passage
• 使用question的连续向量表示，和passage的二进制表示的重排。

Related Work

Retrieval for Open-domain QA

open-domain QA模型使用retriever从知识库中选择出相关的段落。
早期有使用稀疏表示的模型作为retriever，最近更多的使用基于神经网络的稠密表示。DPR是稠密检索的最新SOTA模型。也有使用降维量化操作来减少存储损失的相关工作。
作者的任务是对DPR模型的扩展研究，将learning-to-hash模型和多任务目标结合在一起，在不减少精度的情况下将索引压缩，减少内存占用

Learning To Hash

哈希的目的是使用二进制的编码表示数据，减少搜索的内存和时间开销。
哈希函数本质上是一个映射函数，以一种数据依赖的方式学习哈希函数，将样本表示为一个固定长度的二进制编码。
哈希方法的目标是得到二值编码，简单来说就是将连续的数值转化为离散的二进制取值，但是直接离散的方法无法使用梯度下降算法进行优化。因此为了简化问题，通用的做法是采取更加宽松的约束，不要求二值码是二值的，而是经过松弛后控制在一定的范围内即可。在训练结束后，对松弛的二值码进行量化，最终就会得到离散的二值分布。
Learning to hash主要是通过数据学习到hash函数，最近有很多使用深度学习，通过最小化相似对象的汉明距离，最大化不相似对象的汉明距离，利用端到端的方式学习到哈希函数表示。

Model

简要介绍DPR模型以及BPR模型

DPR(Dense Passage Retriever)

DPR使用两个独立的BERT编码器，将问题q和段落p编码为d维的连续向量表示。

\[e_q=BERT_q(q), e_p=BERT_p(p) \]

对于段落编码，将题目和文本进行连接为: ([CLS] title [SEP] passage [SEP])。选择BERT的CLS输出作为向量表示。在搜索阶段采用内积搜索的方式，检索出对应的段落。

DPR training

DPR训练的目标函数如下：
\(D=\{<q_i, p_i^+, p_{i,1}^-,...,p_{i,n}^->\}_{i=1}^m\) 包含有m个实例，每一个实例包含一个相似的问题\(q_i\)和一个相关的段落\(p_i^+\)，以及n个不相关的段落\(p_{i,j}^-\)，将损失函数定义为正样本的负对数似然。

\[L(q_i,p_i^+,p_{i,1}^-,...,p_{i,n}^-)=-log\frac{e^{sim(q_i, p_i^+)}}{e^{sim(q_i, p_i^+)}+\sum_{j=1}^n e^{sim(q_i, p_{i,j}^-)}} \]

DPR Inference

训练完成后，DPR通过段落编码器为段落创建索引。在运行时，通过问题编码器得到问题的向量表示，然后使用最大内积搜索检索出top-k个段落。

BPR Model

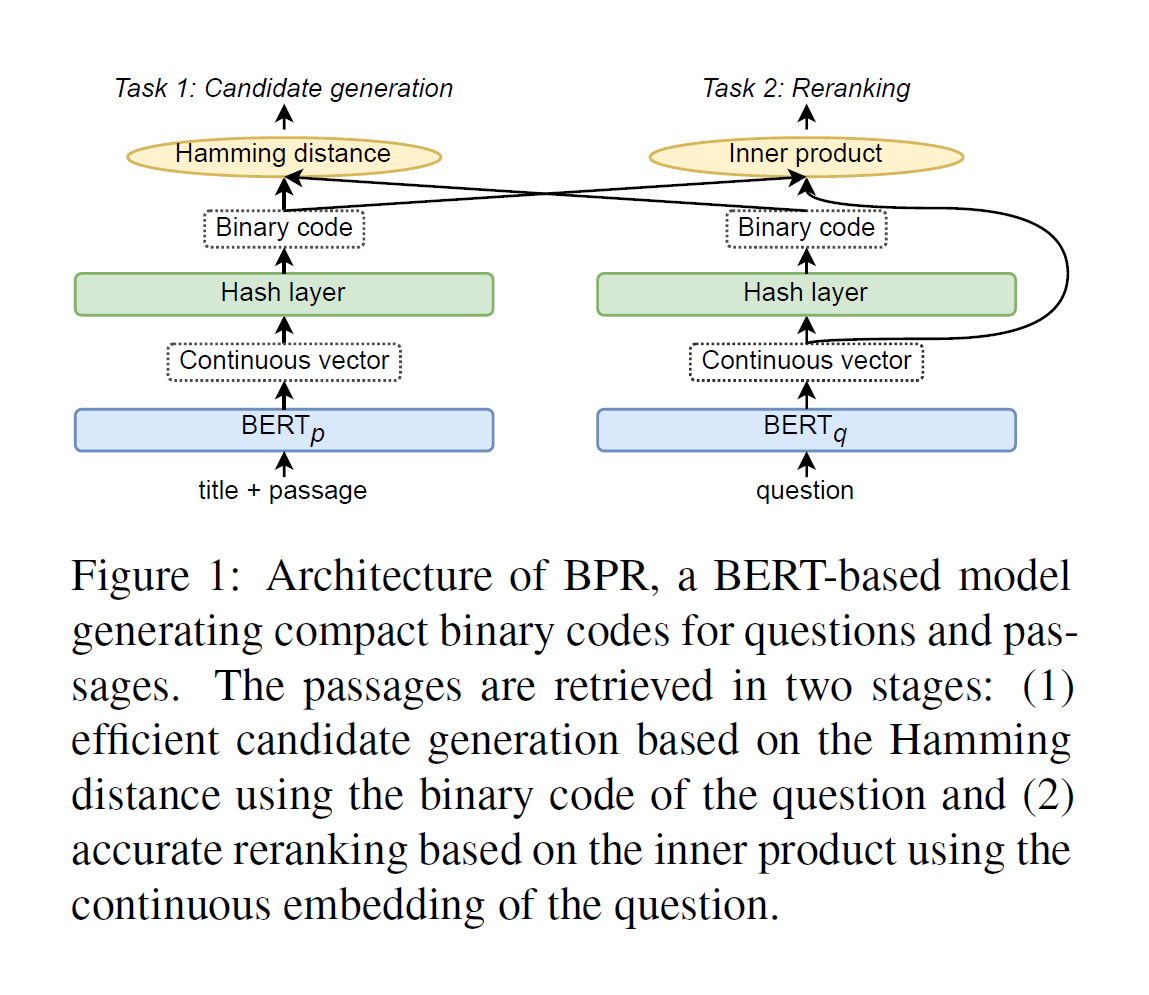
BPR和DPR不同的是将段落索引建立为二元的编码方式。
作者在编码器的上面一层添加了一个hash layer，将编码器的输出通过哈希层转化为二元编码方式。

对于一个稠密向量\(e \in R^d\),哈希层主要是计算出二元的编码\(h \in \{-1,1\}^d\)

\[h=sign(e) \]

但是由于符号函数在不等于0的时候梯度为零，无法进行反向传播。作者在训练的时候使用放缩双曲正切函数。

\[h=tanh(\beta e) \]

\[\beta=\sqrt {\gamma \cdot {step} +1} \]

\(\beta\)相当于扩展参数，当随着训练步骤的迭代，\(\beta\)增加的时候，h函数会逐渐趋于符号函数。
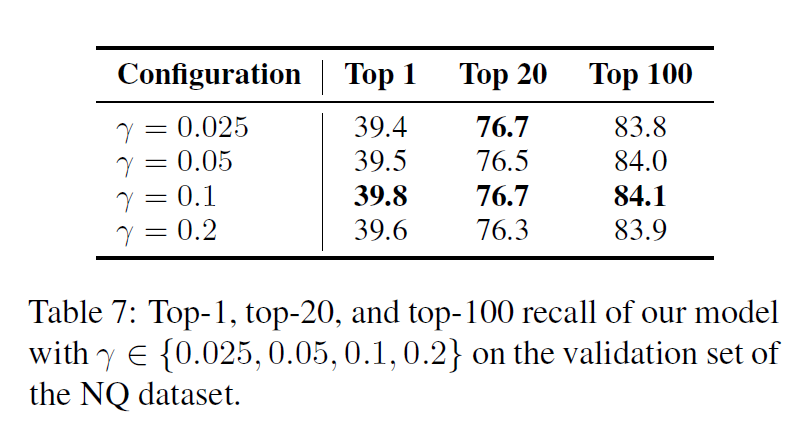
作者在这里探究了\(\gamma\)对于最终结果的影响，可以看到影响不大。

Two-stage Approach

为了能够在保证精度的同时降低计算的损耗，BPR设置了候选段落产生和重新排序两个任务。
在产生候选段落阶段，使用汉明距离计算问题二进制编码\(h_q\)和段落的二进制编码\(h_p\)，得到top-l个候选段落。

然后使用点积计算问题的稠密连续向量\(e_q\)和段落的二进制编码\(h_p\)，然后选择出top-k个段落。

Training

作者将两个阶段的任务loss相加，作为最终的loss

\[L=L_{cand}+L_{rerank} \]

Task 1 Candidate Generation

该任务的目标是通过排序损失来提升候选段落的性能。

\[L_{cand}=\sum_{j=1}^n max(0, <h_{q_i},h_{p_i^+}>+\alpha-<h_{q_i},h_{p_{i,j}^-}>) \]

作者在这里设置α=2
基于汉明距离的检索性能可以使用这个损失函数进行优化，因为汉明距离和内积可以在二进制编码中可以互换使用。

\[dist_H(h_i, h_j)=\frac 1 2 (const-<h_i,h_j>) \]

Task 2 Reranking

使用负对数似然函数优化重排阶段，对问题的连续向量表示和段落的hash表示进行重排训练

\[L_{rerank}=-log\frac{e^{<e_{q_i}, h_{p_i^+}>}}{e^{<e_{q_i}, h_{p_i^+}>}+\sum_{j=1}^n e^{<e_{q_i}, e_{p_{i,j}^-}>}} \]

Algorithms for Candidate Generation

在训练完网络后，作者使用两种方法进行哈希查找

• (1)基于高效的汉明距离计算线性扫描 (CPU计算) (基于矩阵形式的运算)
• (2)建立一个哈希表, 哈希表查找实施每个二进制编码映射到相应的段落。多次查询, 增加汉明半径,直到获得l个段落。

Experiments

Datasets

使用NQ和TQA数据集和英语维基百科作为知识来源进行实验。我们使用DPR网站上提供的以下预处理数据:包含21M篇文章的Wikipedia语料库和检索器的训练/验证数据集，每个问题包含多个正样本、随机负样本和困难负样本段落。

Baselines

使用DPR(线性扫描)，DPR+HSNW(Hierarchical Nevigable Small World)，使用后续量化编码的方式创建DPR索引DPR+simple LSH、DPR+PQ

HSNW：是图论查找算法中的经典模型，通过构建层级NSW，对点进行高效查询。
详细介绍一文看懂HNSW算法理论的来龙去脉_CNU小学生的博客-CSDN博客_hnsw算法
Simple LSH(Simple Locality sensitive hashing)和PQ(Product Quantization)是对DPR的索引进行适当的量化

Experimental settings

在top-k的召回率，检索效率(索引大小和检索时间)进行评估。
同时作者使用和DPR相同的阅读器评估模型的精确匹配精度(QA Acc.EM)。

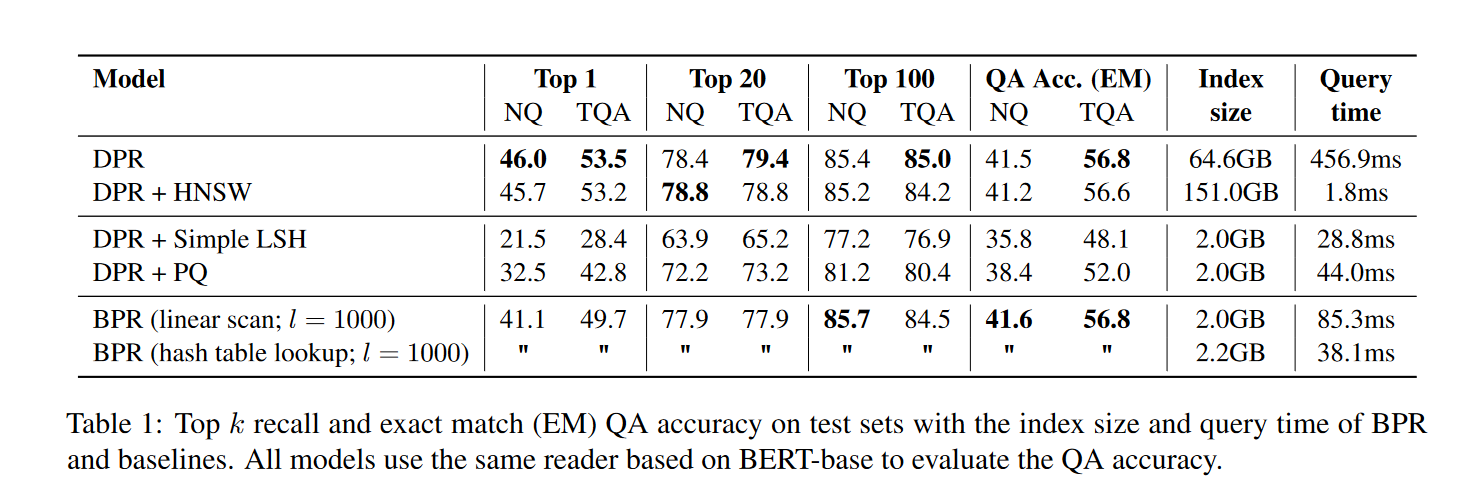
Ablations

作者做了关于重新排序和产生候选集的消融实验，证明任务设置的合理性。

Comparison with SOTA

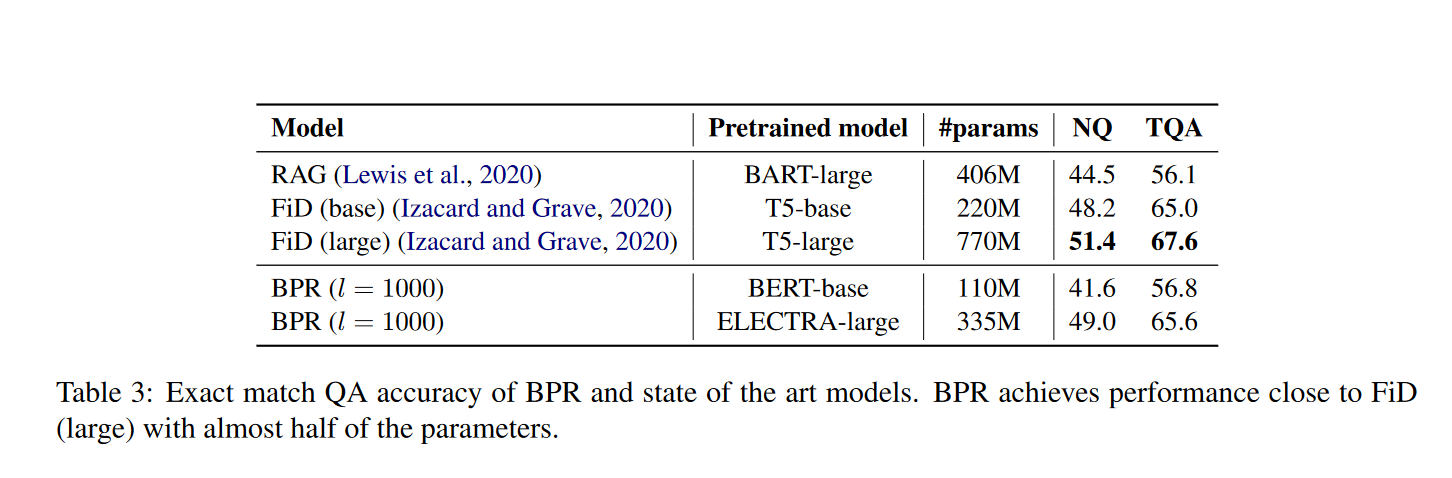
作者将BPR模型结合大规模的阅读器模型ELECTRA-large，与精确匹配的SOTA模型FiD相比，精度稍微落后，但是在模型参数方面只有FiD的一半。

Conclusion

作者提出了使用learning to hash，通过合理的设置多任务，在保证检索精度的同时，大大减少了open-domain QA任务中的检索损耗。
创新点有两个方面

• LTR和段落检索的结合，为减少检索损耗提供了一种新思路
• 作者通过多任务的训练，保证了BPR模型的精度