[2021 Spring] CS61A 学习笔记 lecture 11 Sequences (II) and Data Abstraction

课本： http://composingprograms.com/pages/22-data-abstraction.html
这节课主要内容是序列的特性和数据抽象。

目录

• Sequence(II)
  • Multiple Variables
  • Two Iterations at Once!（zip函数）
  • Modifying Lists
  • List Comprehensions
  • exercise
• Data Abstraction
  • Philosophy
  • Classification
  • Rational Numbers
  • Layers of Abstraction

Sequence(II)

Multiple Variables

for循环中的迭代变量就像是赋值语句的左半边式子：

Two Iterations at Once!（zip函数）

zip函数可以将多个序列进行组合，实际上返回一个生成器

Modifying Lists

列表是可变序列，可以分配元素和切片。

List Comprehensions

列表的完整形式：
[<expression> for <var> in <sequence expression> if <boolean expression>]

exercise

def matches(a, b):
    """Return the number of values k such that A[k] == B[k].
    >>> matches([1, 2, 3, 4, 5], [3, 2, 3, 0, 5])
    3
    >>> matches("abdomens", "indolence")
    4
    >>> matches("abcd", "dcba")
    0
    >>> matches("abcde", "edcba")
    1
    >>> matches("abcdefg", "edcba")
    1
    """
    return sum([1 for x, y in zip(a, b) if x==y])

def triangle(n):
    """Assuming N >= 0, return the list consisting of N lists:
    [1], [1, 2], [1, 2, 3], ... [1, 2, ... N].
    >>> triangle(0)
    []
    >>> triangle(1)
    [[1]]
    >>> triangle(5)
    [[1], [1, 2], [1, 2, 3], [1, 2, 3, 4], [1, 2, 3, 4, 5]]
    """
    return [list(range(1, i + 1)) for i in range(1, n+1)]

Data Abstraction

Philosophy

ADT（abstract data type）: 抽象数据类型

Classification

分类：构造器、访问器、修改器

Rational Numbers

书中将有理数作为ADT的例子。

# Rationals

from math import gcd

def make_rat(n, d):
    """The rational number N/D, assuming N, D are integers, D!=0"""
    g = gcd(n, d)
    n //= g; d //= g
    return (n, d)

def numer(r):
    """The numerator of rational number R in lowest terms."""
    return r[0]

def denom(r):
    """The denominator of rational number R in lowest terms.
       Always positive."""
    return r[1]

def add_rat(x, y):
    return make_rat(numer(x) * denom(y) + numer(y) * denom(x),
                    denom(x) * denom(y))

def mul_rat(x, y):
    return make_rat(numer(x) * numer(y), denom(x) * denom(y))

def str_rat(r):  # (For fun: a little new Python string magic)
    return str(numer(r)) if denom(r) == 1 else f"{numer(r)}/{denom(r)}" 

def equal_rat(x, y):
    return numer(x) * denom(y) == numer(y) * denom(x)

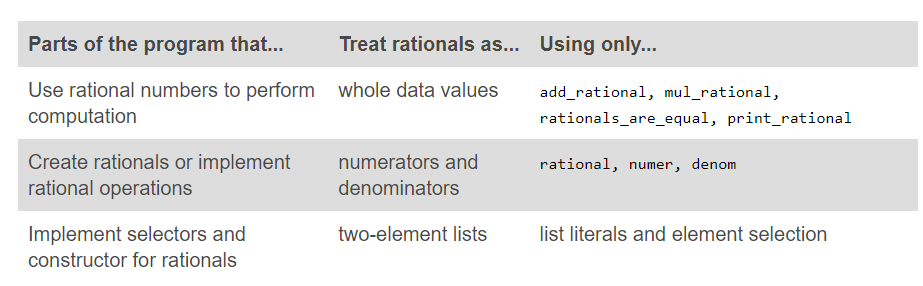
Layers of Abstraction

抽象界限：界限上层不会用到下层的操作，界限下层只用到上一层的操作。