[2021 spring] CS61A Lab 3: Recursion, Tree Recursion

lab03： https://inst.eecs.berkeley.edu/~cs61a/sp21/lab/lab03/#topics

目录

• Topics
  • Recursion
  • Tree Recursion
• Coding practice
  • Q3: Summation
  • Q4: Pascal's Triangle
  • Q5: Repeated, repeated

Topics

Recursion

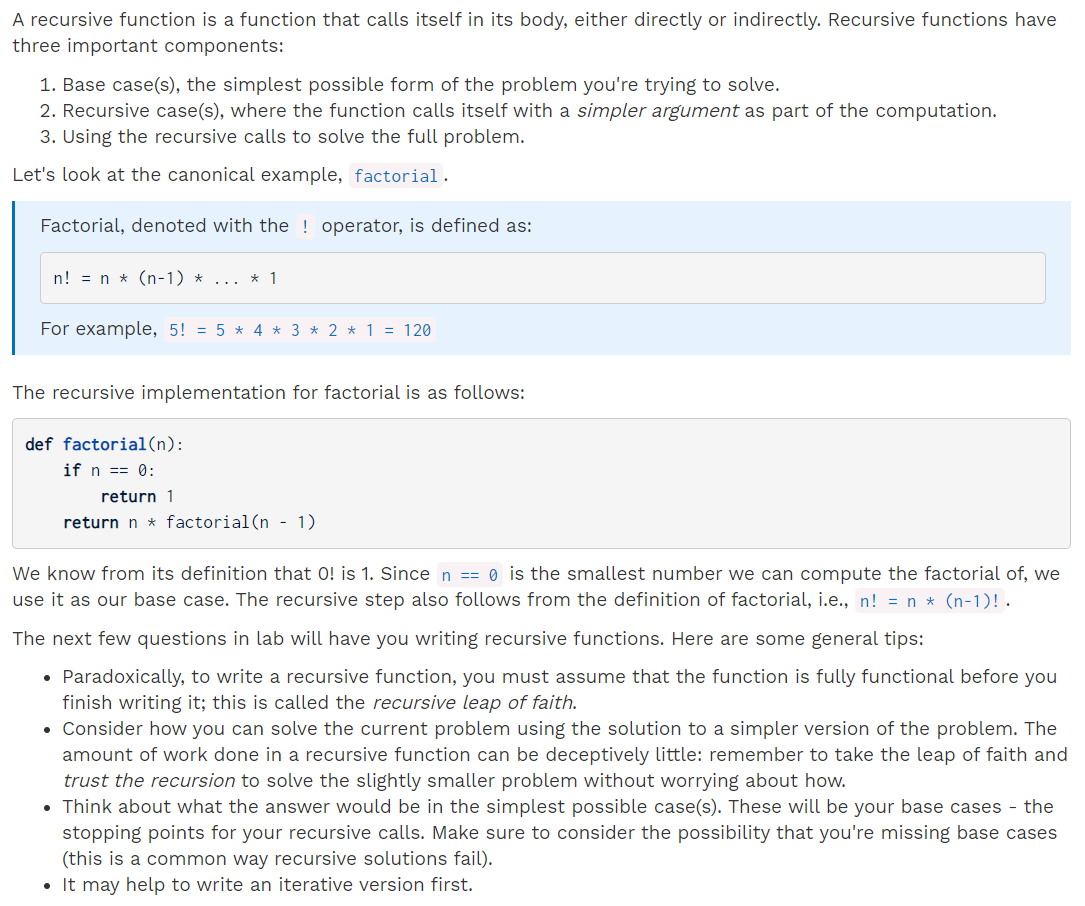
递归函数是在其主体中直接或间接调用自身的函数。 递归函数具有三个重要组成部分：

• 基本案例，您尝试解决的问题的最简单形式。
• 递归情况，其中函数使用更简单的参数调用自身作为计算的一部分。
• 使用递归调用来解决完整的问题。

通用技巧（机翻）：

• 要编写递归函数，你必须在编写完成之前假设该函数是全功能的； 这被称为信仰的递归飞跃。
• 考虑如何使用更简单版本的问题的解决方案来解决当前问题。 在递归函数中完成的工作量可能很少：记住要大胆地相信递归可以解决稍微小的问题，而不必担心如何解决。
• 想想在最简单的情况下答案是什么。 这些将是你的基本情况 - 你递归调用的停止点。 确保考虑你缺少基本情况的可能性（这是递归解决方案失败的常见方式）。
• 首先编写一个迭代版本可能会有所帮助。
  

Tree Recursion

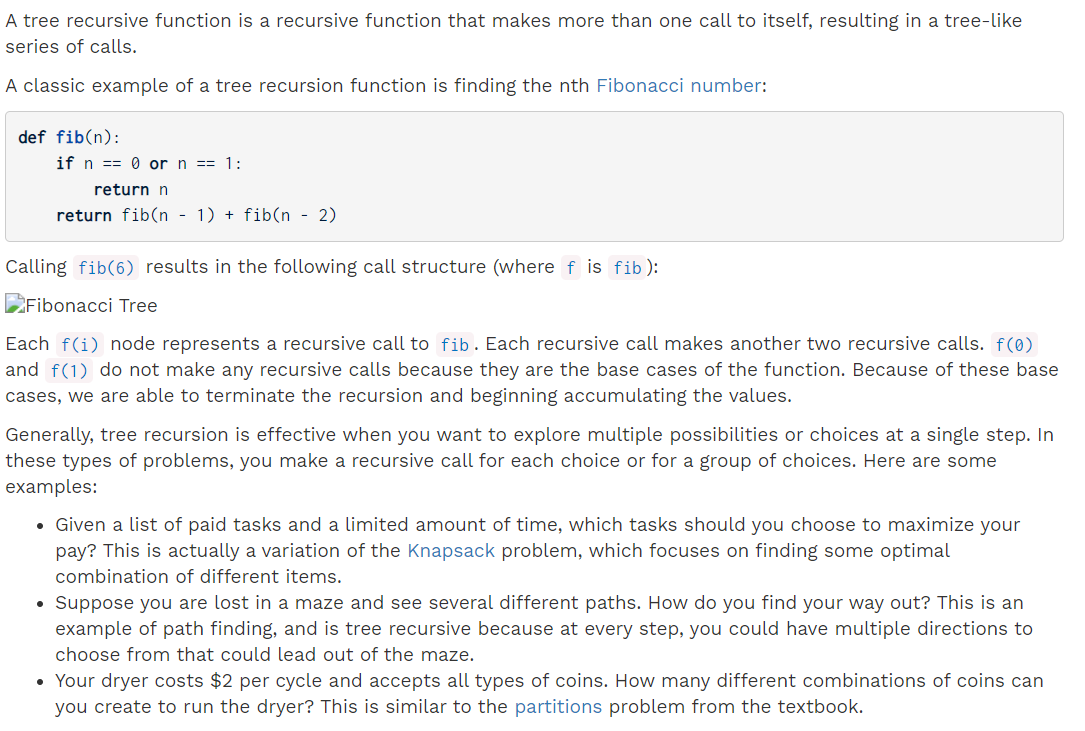
树递归函数是一种递归函数，它对自身进行多次调用，从而产生一系列类似树的调用。
（以斐波那契数列为例）
通常，当您想在一个步骤中探索多种可能性或选择时，树递归是有效的。 在这些类型的问题中，您对每个选择或一组选择进行递归调用。 这里有些例子：

• 给定一份付费任务列表和有限的时间，您应该选择哪些任务来最大化您的报酬？ 这实际上是背包问题的一种变体，它侧重于寻找不同物品的最佳组合。
• 假设您迷失在迷宫中并看到了几条不同的路径。 你如何找到出路？ 这是路径查找的一个示例，并且是树递归的，因为在每一步，您都可以有多个方向可供选择，从而可以走出迷宫。
• 您的烘干机每个周期收费 2 美元，可以接受所有类型的硬币。 您可以创建多少种不同的硬币组合来运行烘干机？ 这类似于教科书中的分区问题。
  

Coding practice

Q3: Summation

def summation(n, term):
    """Return the sum of numbers 1 through n (including n) wíth term applied to each number.
    Implement using recursion!

    >>> summation(5, lambda x: x * x * x) # 1^3 + 2^3 + 3^3 + 4^3 + 5^3
    225
    >>> summation(9, lambda x: x + 1) # 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
    54
    >>> summation(5, lambda x: 2**x) # 2^1 + 2^2 + 2^3 + 2^4 + 2^5
    62
    >>> # Do not use while/for loops!
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'summation',
    ...       ['While', 'For'])
    True
    """
    assert n >= 1
    "*** YOUR CODE HERE ***"
    if n == 1:
        return term(1)
    else:
        return summation(n - 1, term) + term(n)

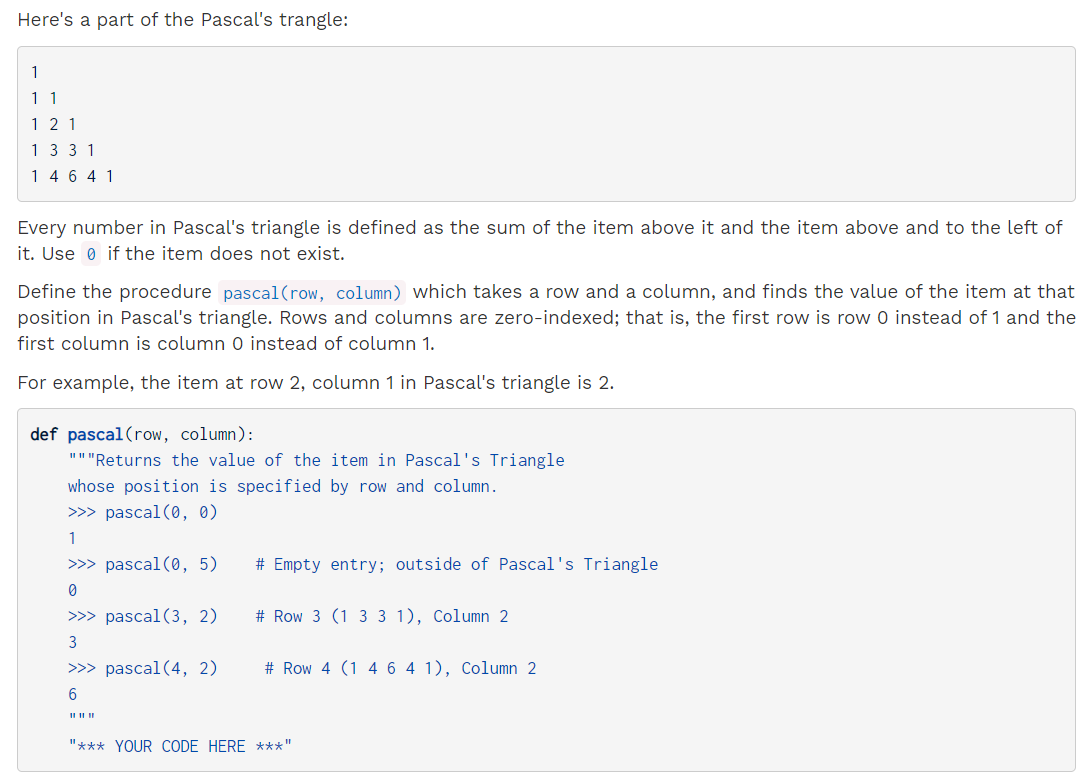
Q4: Pascal's Triangle

def pascal(row, column):
    """Returns the value of the item in Pascal's Triangle 
    whose position is specified by row and column.
    >>> pascal(0, 0)
    1
    >>> pascal(0, 5)	# Empty entry; outside of Pascal's Triangle
    0
    >>> pascal(3, 2)	# Row 3 (1 3 3 1), Column 2
    3
    >>> pascal(4, 2)     # Row 4 (1 4 6 4 1), Column 2
    6
    """
    "*** YOUR CODE HERE ***"
    if column == 0 or row == column:
        return 1 
    elif row < column:
        return 0
    else:
        return pascal(row - 1, column - 1) + pascal(row - 1, column)

Q5: Repeated, repeated

def repeated(f, n):
    """Returns a function that takes in an integer and computes 
    the nth application of f on that integer.
    Implement using recursion!

    >>> add_three = repeated(lambda x: x + 1, 3)
    >>> add_three(5)
    8
    >>> square = lambda x: x ** 2
    >>> repeated(square, 2)(5) # square(square(5))
    625
    >>> repeated(square, 4)(5) # square(square(square(square(5))))
    152587890625
    >>> repeated(square, 0)(5)
    5
    >>> from construct_check import check
    >>> # ban iteration
    >>> check(HW_SOURCE_FILE, 'repeated',
    ...       ['For', 'While'])
    True
    """
    "*** YOUR CODE HERE ***"
    if n == 0:
        return lambda x: x 
    elif n == 1:
        return f
    else:
        return compose1(f, repeated(f, n - 1))