[2021 Spring] CS61A 学习笔记 lecture 7 tree recursion

lecture7 主要讲树递归、线性递归、尾递归。
课本：http://composingprograms.com/pages/17-recursive-functions.html

目录

• 递归分类
• 问题 find_zero
  • 尾递归1
  • 尾递归2
  • 线性递归
  • 树递归
• Finding a Path
  • Path-Finding Program
  • is_path Solution
• Counting the Paths
  • num_paths Solution
  • A Change in Problem
  • And a Little Analysis
• Another Recursion Problem: Counting Partitions
  • Identifying the Problem in the Problem
  • Counting Partitions: Code
• Recurrences

递归分类

树递归：每次调用会多次调用自身

线性递归：每次调用最多进行一次递归调用

尾递归：每次调用最多进行一次递归调用，且只执行自身调用（没有其他变量）

关于尾递归的说明，参考StackOverflow上的What is tail recursion。

问题 find_zero

尾递归1

尾递归2

线性递归

树递归

可以调用多次，但是不是必须的

Finding a Path

Path-Finding Program

每一步都要向下移动一格，向左右移动不超过一格。

is_path Solution

def is_path(blocked, x0, y0):
   """True iff there is a path of squares from (X0, Y0) to some 
   square (x1, 0) such that all squares on the path (including first and
   last) are unoccupied.  BLOCKED is a predicate such that BLOCKED(x, y) 
   is true iff the grid square at (x, y) is occupied or off the edge.
   Each step of a path goes down one row and 1 or 0 columns left or right."""

   if blocked(x0, y0):
       return False
   elif y0 == 0:
       return True
   else:
       return (is_path(blocked, x0-1, y0-1) 
              or is_path(blocked, x0, y0-1) 
              or is_path(blocked, x0+1, y0-1))

Counting the Paths

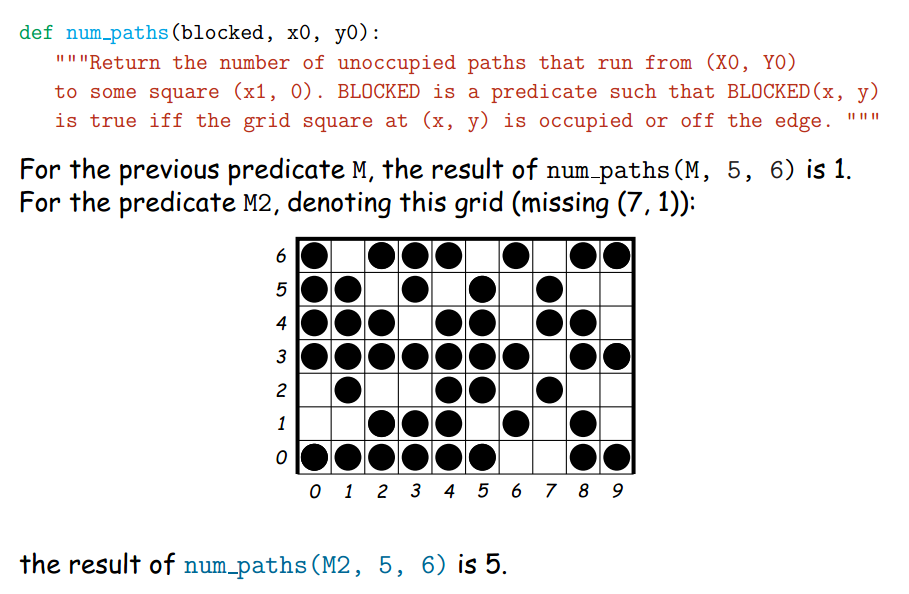
num_paths Solution

def num_paths(blocked, x0, y0):
   """Return the number of unoccupied paths that run from (X0, Y0)
   to some square (x1, 0). BLOCKED is a predicate such that BLOCKED(x, y) 
   is true iff the grid square at (x, y) is occupied or off the edge. """

   if blocked(x0, y0):
       return 0
   elif y0 == 0:
       return 1
   else:
       return num_paths(blocked, x0, y0-1) \
            + num_paths(blocked, x0-1, y0-1) \
            + num_paths(blocked, x0+1, y0-1)
# OR (looking ahead a bit)
#      return sum( (num_paths(blocked, x0+k, y0-1)
#                   for k in range(-1, 2))
#                )

A Change in Problem

change：不限制移动时必须向下移动一格，会导致无限递归

And a Little Analysis

is_path每次调用会调用三次自身，初始y位置为y0，可能的调用次数就可能达到3**y0，指数式增长。

Another Recursion Problem: Counting Partitions

Identifying the Problem in the Problem

Counting Partitions: Code

两种情况：选择k和不选择k

def num_partitions(n, k):
    """Return number of distinct ways to express N as a sum of 
    positive integers each of which is <= K, where K > 0."""
    if n < 0:
        return 0
    elif k == 1:
        return 1
    else:
        return num_partitions(n-k, k) + num_partitions(n, k-1)

Recurrences

斐波那契递归，复杂度很高，简化方法后面会讲到。