RSSI 平面 三点定位算法（C语言、JS源码例程）

目录

• 前言
  • 安卓app实例
• 图示
• 公式
  • 公式推导
• 源码
  • C语言
  • JavaScript
• 测试
  • 测试代码
  • 不平行xy轴3参考点，随机生成交点p(x,y)
    • 示例图
    • 测试数据全为整数
    • 3参考点改为小数
    • 参考点和交点都为小数情况
  • 3参考点构成的三角形其一边平行x或y轴，随机生成交点p(x,y)
    • 示例图
    • 一条边平行于x轴，交点随机生成
    • 交点位置位于 2参考点构成的平行于x轴的同一直线上
  • 3参考点构成的三角形其两边分别平行xy轴，随机生成交点p(x,y)
    • 示例图
• 补充实例
  • 代码优化
  • 三维测试

前言

本来还想着网上找个现成的直接用。。。没想到居然转了转全是错的，有的图画着三点+三边定位第四点，代码实现的三点求三角形重心还是垂直平分线的交点来着，总之都用不了😓。不过算法本身是没有问题的，那么以下就是我根据公式自己计算出的第四点坐标。
☀️前提条件：

1. 三个参考点坐标已知
2. 三个参考点和第四点的距离已知
3. 三个参考点连成的三角形其两边（直角三角形的直角边）不能平行于xy坐标轴
4. 三个参考点连成的三角形其一边平行于xy坐标轴时，只有极少情况可以适用（具体有待数学大佬分析）

补充RSSI测距算法（下图转自：https://blog.csdn.net/u011958166/article/details/106410888）：

安卓app实例

Cordova 使用 cordova-plugin-ble-central 蓝牙插件，实现蓝牙设备持续扫描，打印RSSI等信息 RSSI三点定位 demo
apk下载：码云仓库
V2.2版本效果图

图示

理想情况，rssi算出的距离刚好三个构成的圆交于一点。

普遍情况1，三个圆交出一个范围

普遍情况2，三个圆不想交

普遍情况3，脚踏两条船

情况4，我套你猴子

情况5，孤立

情况6，拉手手

情况7，相切三角阵

情况8，三代人

情况9，箭靶

情况10，苍ying

差不多了，有空接着更

公式

图片转自：https://blog.csdn.net/Luuunatic/article/details/108100569
基于理想情况，三圆交于一点

公式推导

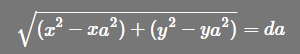
左右平方2

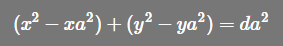
去括号

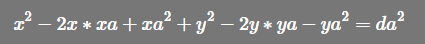
同理b也可以求出

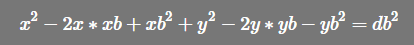
a式-b式，去除x^2 和 y^2，得到二元一次方程式

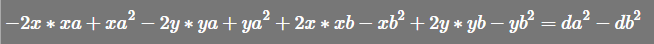
移项得

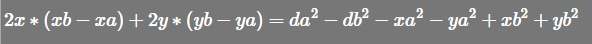
同除以 x或y的乘项，得到 x+某y 或 某x+y


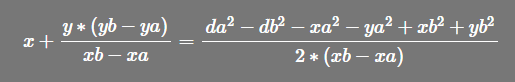
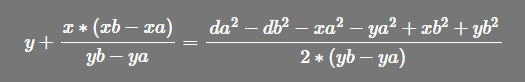
同理推出 a式-c式


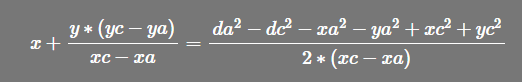
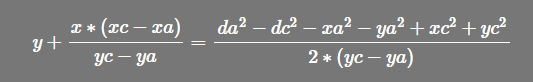
再使用 （a式-b式）- （a式-c式），减掉对应的x 或 y，从而进行求解 y 或 x


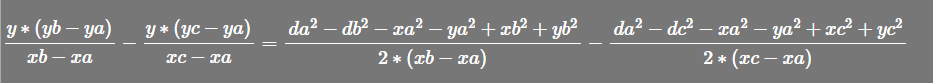
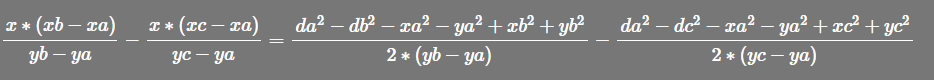
再提出 x 或 y的乘项除掉

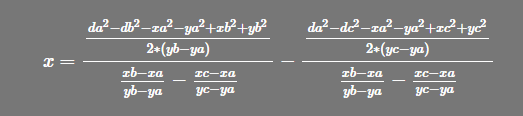
LaTEX公式：\frac{x*(xb-xa)}{yb-ya}-\frac{x*(xc-xa)}{yc-ya}=\frac{da^2-db^2-xa^2-ya^2+xb^2+yb^2}{2*(yb-ya)}-\frac{da^2-dc^2-xa^2-ya^2+xc^2+yc^2}{2*(yc-ya)}

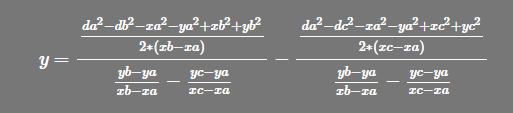
简化就不做了，因为程序实现已经到此为止了。此时我们就可以求出x和y了，再算出 （a式-b式）- （b式-c式）和 （a式-c式）- （b式-c式）的x和y，一共三组 x 和 y，代码中为temp_x[i]和temp_y[i]。
❗❗❗需要注意的是除数为0的情况那么公式就不在成立，所以 三个参考点连成的三角形其两边（直角三角形的直角边）不能平行于xy坐标轴！！！

for(i = 0; i < 3; i++)
{
	j = (i + 1) > 2 ? 2 : (i + 1);
	k = k > 1 ? 0 : k;
	if(x_divide_y[k] - x_divide_y[j] != 0)
	{
		temp_x[i] = (dxyy[k] - dxyy[j]) / (x_divide_y[k] - x_divide_y[j]);
		temp_y[i] = (dxyx[k] - dxyx[j]) / (y_divide_x[k] - y_divide_x[j]);
	}
	else
	{
		temp_x[i] = 0;
		temp_y[i] = 0;
	}

	// printf("temp_x[%d]:%lf, temp_y:%lf\n", i, temp_x[i], temp_y[i]); 
}

最后再对三组数据求平均得出最终结果 x 和 y。

x = (temp_x[0] + temp_x[1] + temp_x[2]) / 3;
y = (temp_y[0] + temp_y[1] + temp_y[2]) / 3;

源码

C语言

#include <stdio.h>
#include <conio.h>
#include <math.h>

int main(void)
{
	/*
		说明：参考的三点坐标及距离位置点的距离。
		不适用情况：三个参考点连成的三角形其两边（直角三角形的直角边）不能平行于xy坐标轴，例如p1(0,0),p2(3,0),p3(0,4),交点(3,4)
		测试数据：p1(0,0),p2(3,4),p3(6,0),交点(6,8)
	*/
	double ref_x[3] = {0, 3, 6};
	double ref_y[3] = {0, 4, 0};
	double ref_d[3] = {4, 3, 4};
	// 计算出的三组 (d[i]方-d[j]方-x[i]方+y[j]方+x[j]方-y[i]方)/(2*(x[j]-x[i]))
	double dxyx[3];
	// 计算出的三组 (d[i]方-d[j]方-x[i]方+y[j]方+x[j]方-y[i]方)/(2*(y[j]-y[i]))
	double dxyy[3];
	// 计算出的三组 (x[i]-x[j])/(y[i]-y[j])
	double x_divide_y[3];
	// 计算出的三组 (y[i]-y[j])/(x[i]-x[j])
	double y_divide_x[3];
	// 计算出的三组x y坐标
	double temp_x[3], temp_y[3];
	// 平均x y坐标
	double x = 0, y = 0;
	int i = 0, j = 0, k = 0;

	for(i = 0; i < 3; i++)
	{
		printf("p[%d](%lf, %lf), dis=%lf\n", i, ref_x[i], ref_y[i], ref_d[i]);

		j = (i + 1) > 2 ? 2 : (i + 1);
		k = k > 1 ? 0 : k;

		// printf("i=%d,j=%d,k=%d\n", i , j , k);

		// printf("numerator:%lf\n", (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]));

		if(ref_x[j] - ref_x[k] != 0) 
			dxyx[i] = (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]) / 2 /(ref_x[j] - ref_x[k]);
		else
			dxyx[i] = 0;

		if(ref_y[j] - ref_y[k] != 0) 
			dxyy[i] = (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]) / 2 /(ref_y[j] - ref_y[k]);
		else
			dxyy[i] = 0;

		if(ref_y[j] - ref_y[k] != 0)
			x_divide_y[i] = (ref_x[j] - ref_x[k]) / (ref_y[j] - ref_y[k]);
		else
			x_divide_y[i] = 0;

		if(ref_x[j] - ref_x[k] != 0)
			y_divide_x[i] = (ref_y[j] - ref_y[k]) / (ref_x[j] - ref_x[k]);
		else
			y_divide_x[i] = 0;

		// printf("dxyx[%d]:%lf, dxyy[%d]:%lf, ", i, dxyx[i], i, dxyy[i]);
		// printf("x_divide_y[%d]:%lf, y_divide_x[%d]:%lf\n", i, x_divide_y[i], i, y_divide_x[i]);

		k++;
	}

	j = 0;
	k = 0;
	for(i = 0; i < 3; i++)
	{
		j = (i + 1) > 2 ? 2 : (i + 1);
		k = k > 1 ? 0 : k;
		if(x_divide_y[k] - x_divide_y[j] != 0)
		{
			temp_x[i] = (dxyy[k] - dxyy[j]) / (x_divide_y[k] - x_divide_y[j]);
			temp_y[i] = (dxyx[k] - dxyx[j]) / (y_divide_x[k] - y_divide_x[j]);
		}
		else
		{
			temp_x[i] = 0;
			temp_y[i] = 0;
		}

		// printf("temp_x[%d]:%lf, temp_y[%d]:%lf\n", i, temp_x[i], i, temp_y[i]); 
	}
	
	x = (temp_x[0] + temp_x[1] + temp_x[2]) / 3;
	y = (temp_y[0] + temp_y[1] + temp_y[2]) / 3;

	printf("\n[ x:%lf, y:%lf ]\n", x, y); 
	
	getchar();

    return 0;
}

JavaScript

// 三点定位函数，分别传入 参考点a、b、c的x、y坐标、待测点与参考点a的距离
function threePointLocation(ax, ay, ad, bx, by, bd, cx, cy, cd)
{
	/*
		说明：参考的三点坐标及距离位置点的距离。
		不适用情况：三个参考点连成的三角形其两边（直角三角形的直角边）不能平行于xy坐标轴，例如p1(0,0),p2(3,0),p3(0,4),交点(3,4)
		测试数据：p1(0,0),p2(3,4),p3(6,0),交点(6,8)
	*/
	//var ref_x = [0, 3, 6];
	//var ref_y = [0, 4, 0];
	//var ref_d = [4, 3, 4];
	var ref_x = [];
	var ref_y = [];
	var ref_d = [];
	// 计算出的三组 (d[i]方-d[j]方-x[i]方+y[j]方+x[j]方-y[i]方)/(2*(x[j]-x[i]))
	var dxyx = [];
	// 计算出的三组 (d[i]方-d[j]方-x[i]方+y[j]方+x[j]方-y[i]方)/(2*(y[j]-y[i]))
	var dxyy = [];
	// 计算出的三组 (x[i]-x[j])/(y[i]-y[j])
	var x_divide_y = [];
	// 计算出的三组 (y[i]-y[j])/(x[i]-x[j])
	var y_divide_x = [];
	// 计算出的三组x y坐标
	var temp_x = [], temp_y = [];
	// 平均x y坐标
	var x = 0, y = 0;
	var i = 0, j = 0, k = 0;
	// 存储交点p坐标
	var p = JSON.parse("{\"x\": 0, \"y\": 0}");
	
	// 初始化数据
	ref_x.push(ax, bx, cx);
	ref_y.push(ay, by, cy);
	ref_d.push(ad, bd, cd);

	for(i = 0; i < 3; i++)
	{
		//console.log("p[" + i +"](" + ref_x[i] + ", " + ref_y[i] + "), dis=" + ref_d[i] + "\n");

		j = (i + 1) > 2 ? 2 : (i + 1);
		k = k > 1 ? 0 : k;
		
		//console.log("numerator:" + (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]));


		if(ref_x[j] - ref_x[k] != 0) 
			dxyx[i] = (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]) / 2 /(ref_x[j] - ref_x[k]);
		else
			dxyx[i] = 0;

		if(ref_y[j] - ref_y[k] != 0) 
			dxyy[i] = (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]) / 2 /(ref_y[j] - ref_y[k]);
		else
			dxyy[i] = 0;

		if(ref_y[j] - ref_y[k] != 0)
			x_divide_y[i] = (ref_x[j] - ref_x[k]) / (ref_y[j] - ref_y[k]);
		else
			x_divide_y[i] = 0;

		if(ref_x[j] - ref_x[k] != 0)
			y_divide_x[i] = (ref_y[j] - ref_y[k]) / (ref_x[j] - ref_x[k]);
		else
			y_divide_x[i] = 0;
			
		//console.log("dxyx[" + i + "]:" + dxyx[i] + ", dxyy[" + i + "]:" + dxyy[i]);
		//console.log("x_divide_y[" + i + "]:" + x_divide_y[i] + ", y_divide_x[" + i + "]:" + y_divide_x[i]);

		k++;
	}

	j = 0;
	k = 0;
	for(i = 0; i < 3; i++)
	{
		j = (i + 1) > 2 ? 2 : (i + 1);
		k = k > 1 ? 0 : k;
		if(x_divide_y[k] - x_divide_y[j] != 0)
		{
			temp_x[i] = (dxyy[k] - dxyy[j]) / (x_divide_y[k] - x_divide_y[j]);
			temp_y[i] = (dxyx[k] - dxyx[j]) / (y_divide_x[k] - y_divide_x[j]);
		}
		else
		{
			temp_x[i] = 0;
			temp_y[i] = 0;
		}
	}

	x = (temp_x[0] + temp_x[1] + temp_x[2]) / 3;
	y = (temp_y[0] + temp_y[1] + temp_y[2]) / 3;

	// console.log("\n[ x:" + x + ", y:" + y + " ]\n"); 
	
	p.x = x;
	p.y = y;
	
	return p;
}

测试

测试代码

#include <stdio.h>
#include <conio.h>
#include <math.h>
#include <stdlib.h>
#include <time.h>

// 三点定位
void three_point_location(double x1, double y1, double d1, double x2, double y2, double d2, double x3, double y3, double d3)
{
	/*
		说明：参考的三点坐标及距离位置点的距离。
		不适用情况：三个参考点连成的三角形其两边（直角三角形的直角边）不能平行于xy坐标轴，例如p1(0,0),p2(3,0),p3(0,4),交点(3,4)
		测试数据：p1(0,0),p2(3,4),p3(6,0),交点(6,8)
	*/
	double ref_x[3] = {x1, x2, x3};
	double ref_y[3] = {y1, y2, y3};
	double ref_d[3] = {d1, d2, d3};
	// 计算出的三组 (d[i]方-d[j]方-x[i]方+y[j]方+x[j]方-y[i]方)/(2*(x[j]-x[i]))
	double dxyx[3];
	// 计算出的三组 (d[i]方-d[j]方-x[i]方+y[j]方+x[j]方-y[i]方)/(2*(y[j]-y[i]))
	double dxyy[3];
	// 计算出的三组 (x[i]-x[j])/(y[i]-y[j])
	double x_divide_y[3];
	// 计算出的三组 (y[i]-y[j])/(x[i]-x[j])
	double y_divide_x[3];
	// 计算出的三组x y坐标
	double temp_x[3], temp_y[3];
	// 平均x y坐标
	double x = 0, y = 0;
	int i = 0, j = 0, k = 0;

	for(i = 0; i < 3; i++)
	{
		// printf("p[%d](%lf, %lf), dis=%lf\n", i, ref_x[i], ref_y[i], ref_d[i]);

		j = (i + 1) > 2 ? 2 : (i + 1);
		k = k > 1 ? 0 : k;

		// printf("i=%d,j=%d,k=%d\n", i , j , k);

		// printf("numerator:%lf\n", (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]));

		if(ref_x[j] - ref_x[k] != 0) 
			dxyx[i] = (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]) / 2 /(ref_x[j] - ref_x[k]);
		else
			dxyx[i] = 0;

		if(ref_y[j] - ref_y[k] != 0) 
			dxyy[i] = (ref_d[k] * ref_d[k] - ref_d[j] * ref_d[j] - ref_x[k] * ref_x[k] + ref_y[j] * ref_y[j] + ref_x[j] * ref_x[j] - ref_y[k] * ref_y[k]) / 2 /(ref_y[j] - ref_y[k]);
		else
			dxyy[i] = 0;

		if(ref_y[j] - ref_y[k] != 0)
			x_divide_y[i] = (ref_x[j] - ref_x[k]) / (ref_y[j] - ref_y[k]);
		else
			x_divide_y[i] = 0;

		if(ref_x[j] - ref_x[k] != 0)
			y_divide_x[i] = (ref_y[j] - ref_y[k]) / (ref_x[j] - ref_x[k]);
		else
			y_divide_x[i] = 0;

		// printf("dxyx[%d]:%lf, dxyy[%d]:%lf, ", i, dxyx[i], i, dxyy[i]);
		// printf("x_divide_y[%d]:%lf, y_divide_x[%d]:%lf\n", i, x_divide_y[i], i, y_divide_x[i]);

		k++;
	}

	j = 0;
	k = 0;
	for(i = 0; i < 3; i++)
	{
		j = (i + 1) > 2 ? 2 : (i + 1);
		k = k > 1 ? 0 : k;
		if(x_divide_y[k] - x_divide_y[j] != 0)
		{
			temp_x[i] = (dxyy[k] - dxyy[j]) / (x_divide_y[k] - x_divide_y[j]);
			temp_y[i] = (dxyx[k] - dxyx[j]) / (y_divide_x[k] - y_divide_x[j]);
		}
		else
		{
			temp_x[i] = 0;
			temp_y[i] = 0;
		}

		// printf("temp_x[%d]:%lf, temp_y[%d]:%lf\n", i, temp_x[i], i, temp_y[i]); 
	}
	
	x = (temp_x[0] + temp_x[1] + temp_x[2]) / 3;
	y = (temp_y[0] + temp_y[1] + temp_y[2]) / 3;

	printf("ret point( x:%lf, y:%lf )\n", x, y);
}

int main(void)
{
	srand((unsigned int)time(NULL));
	int i = 0, j = 0;
	double x = 0, y = 0;
	double ref_x[3] = {0, 30, 60};
	double ref_y[3] = {0, 70, 40};
	double ref_d[3] = {0, 0, 0};
	for(i=0; i<100; i++)
	{
		x = rand() % 100;
		y = rand() % 100;
		printf("real point( %lf , %lf ) ,", x, y);
		for(j=0; j<3; j++)
			ref_d[j] = sqrt( pow((x - ref_x[j]), 2) + pow((y - ref_y[j]), 2) );
		three_point_location(
			ref_x[0], ref_y[0], ref_d[0],
			ref_x[1], ref_y[1], ref_d[1],
			ref_x[2], ref_y[2], ref_d[2]
		);
	}
	
	getchar();

    return 0;
}

不平行xy轴3参考点，随机生成交点p(x,y)

示例图

测试数据全为整数

整数进行的测试，3参考点信息如下：

double ref_x[3] = {0, 30, 60};
double ref_y[3] = {0, 70, 40};
double ref_d[3] = {0, 0, 0};

效果如下：

3参考点改为小数

效果如下：

参考点和交点都为小数情况

3参考点构成的三角形其一边平行x或y轴，随机生成交点p(x,y)

示例图

一条边平行于x轴，交点随机生成

此时，参考点重合于x轴，可以发现只有y=0时，其结果才能匹配，其他值都是接近，或是有所偏差。

当我们将自设的参考点和交点都进行+1操作时，其结果也有偏差。
❗❗❗这便说明一个问题，即使在2参考点构成直线平行于x或y轴的情况，交点即使在参考点构成的直线上，也不能保证算法正确。重合于xy轴是特殊情况！

微调参考点坐标后，又可正常运算

交点位置位于 2参考点构成的平行于x轴的同一直线上

计算全部正确。

3参考点构成的三角形其两边分别平行xy轴，随机生成交点p(x,y)

示例图

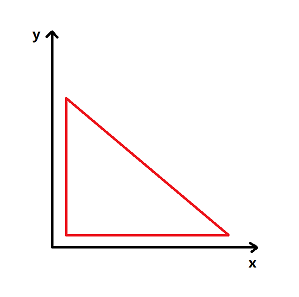
20组数据，无一幸免

补充实例

代码优化

通过先筛选不平行于xy轴的三个参考点

// 判断三个参考点的x或y相减的所有组合是否至少有一组平行于x或y轴，传入三个下标。是则返回1，否则返回0
function isParallelXorY(a, b, c) {
    if(x[a] - x[b] == 0 || x[a] - x[c] == 0 || x[b] - x[c] == 0 || 
        y[a] - y[b] == 0 || y[a] - y[c] == 0 || y[b] - y[c] == 0)
        return 1;
    else
        return 0;
}

配合组合算法，算出所有信号范围内的参考点的所有3组合

// 组合算法参考：https://blog.csdn.net/nanfeibuyi/article/details/79561783
var i = 0, j = 0, t = 0;
var m = 3, n = index;

//用来存储每次算法产生的当前组合
var a = [0, 0, 0];
//第一种组合，a[0]=1,a[1]=2,...a[m-1]=m;
for(i=0; i<m; i++)
{
    a[i] = i+1;
}

//当组合为最后一组时，循环结束；即a[0]=n-m+1,...,a[m-1]=n;j用来判断进位，以及进位之后的调整
for(j=m; a[0]<=(n-m+1); )
{
    //最后一位不断递增，直到达到最大值，产生进位
    for(; a[m-1]<=n; a[m-1]++)
    {
        // 将组合下标传入判断函数，返回0则表示此组合的三个参考点可以做为定位算法使用
        if(0 == isParallelXorY((a[0]-1), (a[1]-1), (a[2]-1)))
        {
            var temp_p = threePointLocation(x[(a[0]-1)], y[(a[0]-1)], d[(a[0]-1)], 
                x[(a[1]-1)], y[(a[1]-1)], d[(a[1]-1)], x[(a[2]-1)], y[(a[2]-1)], d[(a[2]-1)]);
            p.push(temp_p);
            // log("temp_p:(" + temp_p.x + "," + temp_p.y + ")", "log");
        }
    }
    
    //判断a[1]--a[m-2]是否有进位 如果 a[m-1]>n 产生进位
    for(j=m-2; j>=0; j--)
    {
        a[j]++;
        //a[j]不进位,那么a[j-1]也不进位，结束继续判断
        if(a[j] <= (j+n-m+1))
        {
            break;
        }
    }
    
    //调整，使得a[index-1],a[index],a[index]顺序排列，其中a[index]产生进位
    for(j++; j>0 && j<m; j++)
    {
        a[j] = a[j-1]+1;
    }
}

最后再对所有符合条件后算出的坐标集求平均值，得到坐标点

// 存储总和、平均x/y
var sum_x = 0, sum_y = 0, avg_x = 0, avg_y = 0;
for(i=0; i<p.length; i++)
{
    sum_x += p[i].x;
    sum_y += p[i].y;
}
// 计算平均值
if(p.length > 0) {
    avg_x = sum_x / p.length;
    avg_y = sum_y / p.length;

    document.getElementById("coordinate").innerHTML = "坐标：（ "+ avg_x.toFixed(4) + "，" + avg_y.toFixed(4) + "）";
}
else {
    document.getElementById("coordinate").innerHTML = "坐标：（?，?）";
}

三维测试

好像三维中定位二维坐标也勉强能用（有待大佬解释了0.0）

求三维坐标有待研究