剑指offer第二版面试题-Java描述
最近在用Java刷剑指offer(第二版)的面试题。书中原题的代码采用C++编写,有些题的初衷是为了考察C++的指针、模板等特性,这些题使用Java编写有些不合适。但多数题还是考察通用的算法、数据结构以及编程思想等,与语言本身无太大关系。因此在选择编程语言时,我还是选择了Java。好吧,主要是我C++忘得差不多了,仅仅是曾经学过俩月,使用Java顺手一些。后续可能再用Python刷一遍。
github见:https://github.com/ikheu/sword_offer
第2章 面试需要的基础知识
面试题3 数组中重复的数字
题目一:找出数组中重复的数字
- 描述:在长度为n的数组里所有数字都在0~n-1范围内。数组中某些数字是重复的,请找出任意一个重复的数字。如数组{2, 3, 1, 0, 2, 5, 3},输出的重复的数字为2或3。
- 思路:利用数组的索引在0~n-1这个范围的性质,将数字i移至索引i的位置。
- 考点:对数组的理解以及对问题的分析能力。
题目二:不修改数组找出重复的数字
- 描述:在长度为n+1的数组里所有数字都在1~n范围内。找出重复的数字,但不修改数组。
- 思路:当然可完全利用题目一的方法,只是需要辅助空间。不需要辅助空间是最好的了。这里使用二分法,对数组进行计数,逐渐缩小重复的数字所处的范围。
- 考点:对二分查找的灵活应用,毕竟写出正确无误的二分法时有些难度的。同时要重视与面试官的沟通,明确需求,如是否能更改数组,是否可以使用辅助空间等。
package sword_offer; // page 39 数组中重复的数字 public class Solution3 { // 题目1 // 输出数组中重复的数字,空间复杂度O(1),时间复杂度O(n) // 数组长度为n,数字在0~n-1范围内 public static int duplicate(int[] arr) { for (int i = 0; i < arr.length; i++) { //System.out.println(i); while (arr[i] != i) { if (arr[i] == arr[arr[i]]) return arr[i]; else { int temp = arr[i]; arr[i] = arr[temp]; arr[temp] = temp; //System.out.println(Arrays.toString(arr)); } } } return -1; } // 题目2 // 输出数组中重复的数字,空间复杂度O(1),时间复杂度O(nlog(n)) // 数组长度为n+1,数字在1~n范围内,要求不修改数组,并不使用辅助空间 public static int getDuplication(int[] arr) { int start = 1; int end = arr.length - 1; while(end >= start) { int middle = (end - start) / 2 + start; int count = getCount(arr, start, middle); if (end == start) { if (count > 1) return start; else break; } if (count > middle - start + 1) { end = middle; } else start = middle + 1; } return -1; } // 计算数组arr元素处在[start, end]范围内元素个数 private static int getCount(int[] arr, int start, int end) { int count = 0; for (int i = 0; i < arr.length; i++) { if (arr[i] >= start && arr[i] <= end) count++; } return count; } // 测试 public static void main(String[] args) { int[] arr = {1, 2, 3, 1}; System.out.println(duplicate(arr));int[] arr2 = {2, 3, 5, 4, 3, 2, 6, 7}; System.out.println(getDuplication(arr2)); } }
面试题4 二维数组中的查找
- 描述:二维数组中,数字按从左到右、从上到下的顺序递增。给定一个整数,判断该数组中是否含有该整数。
- 思路:从数组的右上角或左下角开始进行查找数据,缩小可能包含该数的范围。
- 考点:画图分析问题,寻求问题的突破口。并能正确编写程序,避免死循环等问题。
例如,从二维数组$\left[ {\begin{array}{*{20}{c}}
{1}&{2}&{8}&9 \\
{1}&{4}&{9}&{12} \\
{4}&{7}&{10}&{13} \\
{6}&{8}&{11}&{15}
\end{array}} \right]$中寻找是否包含数字7。
从右上角查找时,逐渐向左下方缩小范围。红色的代表包含目标值7的区域,过程如下:
$$\left[ {\begin{array}{*{20}{c}}
{\color{red}1}&{\color{red}2}&{\color{red}8}&9 \\
{\color{red}1}&{\color{red}4}&{\color{red}9}&{12} \\
{\color{red}4}&{\color{red}7}&{\color{red}{10}}&{13} \\
{\color{red}6}&{\color{red}8}&{\color{red}{11}}&{15}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{\color{red}1}&{\color{red}2}&{8}&9 \\
{\color{red}1}&{\color{red}4}&{9}&{12} \\
{\color{red}4}&{\color{red}7}&{10}&{13} \\
{\color{red}6}&{\color{red}8}&{11}&{15}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{1}&{2}&{8}&9 \\
{\color{red}1}&{\color{red}4}&{9}&{12} \\
{\color{red}4}&{\color{red}7}&{10}&{13} \\
{\color{red}6}&{\color{red}8}&{11}&{15}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{1}&{2}&{8}&9 \\
{1}&{4}&{9}&{12} \\
{\color{red}4}&{\color{red}7}&{10}&{13} \\
{\color{red}6}&{\color{red}8}&{11}&{15}
\end{array}} \right]$$
从左下角查找时,逐渐向右上方缩小范围。过程如下:
$$\left[ {\begin{array}{*{20}{c}}
{1}&{\color{red}2}&{\color{red}8}&{\color{red}9} \\
{1}&{\color{red}4}&{\color{red}9}&{\color{red}{12}} \\
{4}&{\color{red}7}&{\color{red}{10}}&{\color{red}{13}} \\
{6}&{\color{red}8}&{\color{red}{11}}&{\color{red}{15}}
\end{array}} \right]\to\left[ {\begin{array}{*{20}{c}}
{1}&{\color{red}2}&{\color{red}8}&{\color{red}9} \\
{1}&{\color{red}4}&{\color{red}9}&{\color{red}{12}} \\
{4}&{\color{red}7}&{\color{red}{10}}&{\color{red}{13}} \\
{6}&{8}&{11}&{15}
\end{array}} \right]$$
package sword_offer; // page 44 二维数组中的查找 public class Solution4 { // 从右上角的元素开始查找,逐渐缩小范围 public static boolean findNum(int[][] arr, int target) { boolean found = false; int row = 0; int col = arr[0].length - 1; while (col > 0 && row <= arr.length) { int diff = arr[row][col] - target; if (diff == 0) { found = true; break; } else if (diff > 0) col--; else row++; } return found; } // 测试 public static void main(String[] args) { int[][] arr = {{1,2,8,9},{2,4,9,12},{4,7,10,13},{6,8,11,15}}; System.out.println(findNum(arr, 9)); } }
面试题5 替换空格
- 描述:将字符串中的每个空格替换成%20。如输入"we are fine",输出"we%20are%20fine"。
- 思路:原题考察了C++中指针的操作。Java里数组不可变,因此本题变得没有难度了。利用String对象的.charAt函数遍历每个字符,并使用StringBuilder构建新的字符串。
- 考点:对字符串的处理。
package sword_offer; // page 51 替换空格 public class Solution5 { // 在Java中字符串时不可变的,因而只能构造一个新的字符串。原文中该题的难点也无法体现出来了。 public static String replaceBlank(String str) { StringBuilder strb = new StringBuilder(); for (int i = 0; i < str.length(); i++) { if (str.charAt(i) == ' ') { strb.append("%20"); } else strb.append(str.charAt(i)); } return strb.toString(); } // 测试 public static void main(String[] args) { String str = "We are happr."; System.out.println(replaceBlank(str)); } }
面试题6 从尾到头打印链表
- 描述:输入一个链表的头节点,从尾到头打印每个节点的值。
- 思路:从尾到头打印,即为“先进后出”,则可以使用栈来处理;考虑递归的本质也是一个栈结构,可递归输出。
- 考点:对链表、栈、递归的理解。
package sword_offer; //page 58 从尾到头打印链表 import java.util.Stack; //链表类 class ListNode{ ListNode next = null; int value; public void printOut() { System.out.println(value); ListNode tmp = next; while (tmp != null) { System.out.println(tmp.value); tmp = tmp.next; } } } public class Solution06 { //方法1:使用Stack栈的先push后pop public static void printListReverse(ListNode listNode) { Stack<ListNode> stack = new Stack<ListNode>(); while(listNode != null) { stack.push(listNode); listNode = listNode.next; } while(!stack.isEmpty()) { System.out.println(stack.pop().value); } } //方法2:使用递归的方式,相当于从内部往外部推 public static void printListReverse_rec(ListNode listNode) { if(listNode != null) { if (listNode.next != null) printListReverse_rec(listNode.next); System.out.println(listNode.value); } } //测试 public static void main(String[] args) { ListNode ln1 = new ListNode(); ListNode ln2 = new ListNode(); ListNode ln3 = new ListNode(); ln1.next = ln2; ln2.next = ln3; ln1.value = 1; ln2.value = 2; ln3.value = 3; printListReverse_rec(ln1); printListReverse(ln1); } }
面试题7 重建二叉树
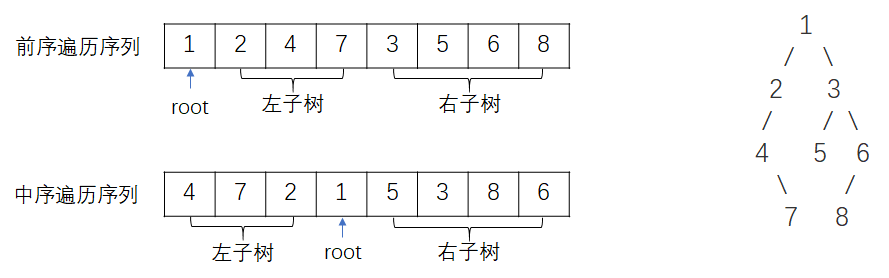
- 描述:输入某二叉树的前序遍历和中序遍历结果,重建该二叉树。假设前序遍历或中序遍历的结果中无重复的数字。
- 思路:前序遍历的第一个元素为根节点的值,据此将中序遍历数组拆分为左子树+root+右子树,前序遍历数组拆分为root+左子树+右子树。再对左右子树进行同样的操作。
- 考点:对二叉树不同遍历方法的掌握。
package sword_offer; // page 62 重建二叉树 // 二叉树类,包含左右子树,以及用于查看的方法 class BinaryTreeNode { int value; BinaryTreeNode leftNode; BinaryTreeNode rightNode; // 中序遍历输出查看 public void printList() { if (leftNode != null) leftNode.printList(); System.out.println(value); if (rightNode != null) rightNode.printList(); } } public class Solution7 { // 重建二叉树函数 public static BinaryTreeNode rebultTree(int[] preorder, int[] inorder) { BinaryTreeNode root = rebultTree(preorder, 0, preorder.length - 1, inorder, 0, inorder.length - 1); return root; }
// 重写函数 private static BinaryTreeNode rebultTree(int[] preorder, int startPre, int endPre, int[] inorder, int startIn, int endIn) { if (startPre > endPre || startIn > endIn) return null; BinaryTreeNode root = new BinaryTreeNode(); root.value = preorder[startPre]; for (int i = startIn; i <= endIn; i++) { if (inorder[i] == preorder[startPre]) { root.leftNode = rebultTree(preorder, startPre + 1, startPre + i - startIn, inorder, startIn, i - 1); root.rightNode = rebultTree(preorder, startPre + i - startIn + 1, endPre, inorder, i + 1, endIn); } } return root; }
// 测试 public static void main(String[] args) { int[] preorder = { 1, 2, 4, 7, 3, 5, 6, 8 }; int[] inorder = { 4, 7, 2, 1, 5, 3, 8, 6 }; BinaryTreeNode root = rebultTree(preorder, inorder); //System.out.println(root.leftNode.rightNode.value); root.printList(); } }
面试题8 二叉树的下一个节点
- 描述:给定一棵二叉树和其中的一个节点,找出中序遍历序列的下一个节点。树中应定义指向左节点、右节点、父节点的三个变量。
- 思路:该节点若存在右节点,右子树的最左节点则为下一节点;若不存在右节点,则向上遍历,直至找到是父节点的左节点的那个节点,该节点的父节点则为下一节点。
- 考点:对中序遍历的理解。
package sword_offer; // page 65 二叉树的下一个节点 // 定义二叉树类,包含左右子树、父节点,以及用于查看的函数 class TreeNode { char value; TreeNode left; TreeNode right; TreeNode father; // 中序遍历输出查看 public void printList() { if (left != null) left.printList(); System.out.println(value); if (right != null) right.printList(); } } public class Solution8 { public static TreeNode findNext(TreeNode node) { // 有右节点,找到右子树的最左节点 if (node.right!= null) { node = node.right; while(node.left != null) node = node.left; return node; } // 无右节点,则向上遍历,直至找到节点为父节点的左子节点 while(node.father != null) { if (node.father.left == node) return node.father; node = node.father; } return null; }
public static void main(String[] args) { // 建立一个二叉树节点的数组,并tree[i].value赋值 TreeNode[] tree = new TreeNode[9]; char[] chars = {'a', 'b', 'c', 'd', 'e', 'f', 'g', 'h', 'i'}; for (int i = 0; i < tree.length; i++) { tree[i] = new TreeNode(); tree[i].value = chars[i]; } /* * a * / \ * b c * / \ / \ * d e f g * / \ * h i */ // 左右节点关系 tree[0].left = tree[1]; tree[0].right = tree[2]; tree[1].left = tree[3]; tree[1].right = tree[4]; tree[2].left = tree[5]; tree[2].right = tree[6]; tree[4].left = tree[7]; tree[4].right = tree[8]; // 父节点关系 tree[1].father = tree[0]; tree[2].father = tree[0]; tree[3].father = tree[1]; tree[4].father = tree[1]; tree[5].father = tree[2]; tree[6].father = tree[2]; tree[7].father = tree[4]; tree[8].father = tree[4]; tree[0].printList(); } }
面试题9 两个栈实现队列
- 描述:使用两个栈实现一个队列。队列中实现尾部插入和头部删除函数。
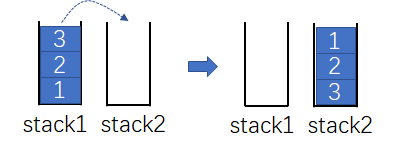
- 思路:栈结构“先进后出”,插入数据时进入第一个栈;删除数据时,将第一个栈的所有数据都弹出到第二个栈,这时原先先插入的数据位于栈的顶端。即可满足队列的“先进先出”。
- 考点:对栈和队列的理解;对泛型的使用等。
package sword_offer; // page 68 两个栈实现队列 import java.util.Stack; // 队列类,包含两个栈、两个操作队列的方法 class Queue <T>{ Stack<T> stack1 = new Stack<>(); Stack<T> stack2 = new Stack<>();
// 插入节点 public void appendTail(T element) { stack1.push(element); }
// 删除节点 public T deleteHead(){ if (stack2.isEmpty()) { while(!stack1.isEmpty()) { T data = stack1.pop(); stack2.push(data); } } // 为空时,输出异常 if (stack2.isEmpty()) throw new IllegalArgumentException("queue is empty"); return stack2.pop(); } }
public class Solution9 { // 测试 public static void main(String[] args) { Queue<Integer> queue = new Queue<>(); queue.appendTail(1); queue.appendTail(2); queue.appendTail(3); System.out.println(queue.deleteHead()); System.out.println(queue.deleteHead()); queue.appendTail(4); System.out.println(queue.deleteHead()); System.out.println(queue.deleteHead()); System.out.println(queue.deleteHead()); } }
面试题10 斐波那契数列
- 描述:计算斐波那契数列的第n项。
- 思路:使用循环从下往上计算数列。
- 考点:考察对递归和循环的选择。使用递归的代码通常比循环简洁,但使用递归时要注意一下几点:1、函数调用的时间和空间消耗;2、递归中的重复计算;3、最严重的栈溢出。根据斐波那契数列递归形式定义很容易直接将代码写成递归,而这种方式有大量重复计算,效率很低。
$$f\left( n \right) = \left\{ \begin{array}{l}
0\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = 0\\
1\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;n = 1\\
f\left( {n - 1} \right) + f\left( {n - 2} \right)\;\;\;\;n > 1
\end{array} \right.$$
package sword_offer; // page 74 斐波那契数列 public class Solution10 { // 获得fibonacci(n) public static long fibonacci(int n) { if (n <= 1) return n; long fibMinusOne = 0; long fibMinusTwo = 1; long fib = 0; for (int i = 2; i <= n; i++) { fib = fibMinusOne + fibMinusTwo; fibMinusOne = fibMinusTwo; fibMinusTwo = fib; } return fib; }
// 测试函数 public static void main(String[] args) { System.out.println(fibonacci(6)); } }
面试题11 旋转数组的最小值
- 描述:把数组开头的一部分移动到数组的末尾得到的数组称为旋转数组。输入一个递增排序的数组的旋转数组,输出数组的最小值。
- 思路:考虑旋转数组的特点,使用二分查找方法逐渐缩小目标值的范围。需要考虑的特殊情况有:数组仅有一个元素的情形;数组未旋转的情形;形如{1,0,1,1,1}的数组需要顺序查找,因为二分查找会跳过最小值。
- 考点:对于新概念的理解;对二分查找的熟练掌握;对不同输入的分析和全面考虑。
package sword_offer; // page 82 旋转数组的最小数字 public class Solution11 { public static int min(int[] arr) { int start = 0; int end = arr.length - 1; if (arr[start] < arr[end]) // 旋转数组是其本身的情形 return arr[start]; while (start <= end) { int mid = start + ((end - start) >> 1); if (arr[mid] == arr[start] && arr[mid] == arr[end]) // 考虑顺序查找情形 return min(arr, start, end); if (arr[mid] >= arr[start]) start = mid; else end = mid; if (start == end - 1) break; } return arr[end]; }
// 特殊情形下的顺序查找 private static int min(int[] arr, int start, int end) { int result = arr[start]; for (int i = start + 1; i <= end; i++) if (arr[i] < result) result = arr[i]; return result; }
// 测试 public static void main(String[] args) { int[] arr = { 4, 5, 1, 2, 3 }; int[] arr2 = { 1, 0 , 1, 1, 1 }; System.out.println(min(arr)); System.out.println(min(arr2)); } }
面试题12 矩阵中的路径
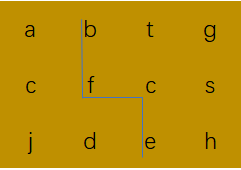
- 描述:判断字符矩阵中是否存在一条包含字符串字符的路径。
- 思路:使用回溯法,上下左右尝试。觉得想写出正确的程序还挺难的。
- 考点:对回溯法的掌握。
package sword_offer; public class Solution12 { public static boolean hasPath(char[][] matrix, String str) { int rows = matrix.length; int cols = matrix[0].length; boolean[][] visited = new boolean[rows][cols]; int pathLength = 0; for (int row = 0; row < rows; row++) { for (int col = 0; col < cols; col++) { if (hasPathCore(matrix, rows, cols, row, col, str, pathLength, visited)) return true; } } return false; } // 上下左右递归搜索 private static boolean hasPathCore(char[][] matrix, int rows, int cols, int row, int col, String str, int pathLength, boolean[][] visited) { boolean hasPath = false; if (pathLength > str.length() - 1) return true; if (row >= 0 && row < rows && col >= 0 && col < cols && matrix[row][col] == str.charAt(pathLength) && !visited[row][col]) { ++pathLength; visited[row][col] = true; hasPath = hasPathCore(matrix, rows, cols, row + 1, col, str, pathLength, visited) || hasPathCore(matrix, rows, cols, row, col + 1, str, pathLength, visited) || hasPathCore(matrix, rows, cols, row - 1, col, str, pathLength, visited) || hasPathCore(matrix, rows, cols, row, col - 1, str, pathLength, visited); if (!hasPath) { --pathLength; visited[row][col] = false; } } return hasPath; } // 测试 public static void main(String[] args) { char[][] matrix = { { 'a', 'b', 't', 'g' }, { 'c', 'f', 'c', 's' }, { 'j', 'd', 'e', 'h' } }; String str = "bfc"; System.out.println(hasPath(matrix, str)); } }
面试题14 剪绳子
- 描述:给一段长度位整数n的绳子,剪成若干段,每段长度也是整数,计算这些长度的乘积的最大值。
- 思路:比较容易想到的动态规划以及乍看起来让人蒙圈的贪婪法。无论是那种方法,能做出来就不容易。
- 考点:抽象建模能力;对动态规划和贪婪发的理解。
package sword_offer; // page 96 剪绳子 import java.lang.Math; public class Solution14 { // 动态规划算法,比较容易想到 public static int maxProduct_s1(int len) { if (len < 2) return 0; if (len == 2) return 1; if (len == 3) return 2; int[] products = new int[len + 1]; products[0] = 0; products[1] = 1; products[2] = 2; products[3] = 3; int max = 0; for (int i = 4; i <= len; i++) { for (int j = 1; j <= i / 2; j++) { int product = products[j] * products[i - j]; if (max < product) max = product; products[i] = max; } } max = products[len]; return max; } // 贪婪算法,很不容易想到 public static int maxProduct_s2(int len) { if (len < 2) return 0; if (len == 2) return 1; if (len == 3) return 2; int times3 = len / 3; if (len - times3 * 3 == 1) times3--; int times2 = (len - times3 * 3) / 2; return (int) (Math.pow(3, times3)) * (int) (Math.pow(2, times2)); } // 测试 public static void main(String[] args) { System.out.println(maxProduct_s1(20)); System.out.println(maxProduct_s2(20)); } }
面试题15 二进制中1的个数
- 描述:输入一个整数,计算该数二进制中1的个数。
- 思路:方法一逐位上移,将1和整数进行与计算;方法二有点奇技淫巧的感觉了,需要想到整数-1后的二进制数特点。在Java里,可以通过Integer.toBinaryString函数查看整数的二进制形式。
- 考点:对二进制的理解,和对位运算的掌握。
package sword_offer; //page 100 二进制中1的个数 public class Solution15 { // 方法1:逐位进行与运算 public static int numOfOne_a(int n) { int flag = 1; int count = 0; while (flag != 0) { if ((n & flag) != 0) count++; flag = flag << 1; } return count; } // 方法二:进行n = (n - 1) & n运算,n含有1的位数减1 public static int numOfOne_b(int n) { int count = 0; while (n != 0) { n = (n - 1) & n; count++; } return count; } // 测试 public static void main(String[] args) { System.out.println(Integer.toBinaryString(10000)); System.out.println(numOfOne_a(10000)); System.out.println(numOfOne_b(10000)); } }
第3章 高质量的代码
面试题16 数值的整数次方
- 描述:构造求数值的整数幂函数。
- 思路:根据整数幂求解的特点,构造高效求解的函数;考虑幂为负整数的情形,以及避免溢出的处理;使用位运算进行除2和判断奇偶。像这种基本的数学函数,竭力提高运算性能总是有必要的。
- 考点:对幂运算的掌握。
package sword_offer; // page 16 数值的整数次方 public class Solution16 { // 幂运算函数,f=x^n,不用考虑大数问题,n可能为负整数 public static double myPow(double x, int n) { if (n == 0) return 1.0; if (n < 0) return 1.0 / (x * myPow(x, -n - 1));// 避免溢出 double result = myPow(x, n >> 1);// 位运算除2 result *= result; if ((n & 1) == 1)// 位运算判断奇偶 result *= x; return result; }
// 测试 public static void main(String[] args) { int a = -2147483648; System.out.println(myPow(1.0, a)); System.out.println(myPow(2.0, 4)); System.out.println(myPow(2.0, 3)); } }
面试题17 打印从1到最大n位数
- 描述:输入数字n,按顺序打印出1到n的十进制数。
- 思路:要意识到是大数问题,可移动符号运算以及数字排列输出两种方式解决。
- 考点:对大数问题的处理;打印数字时要考虑到阅读的习惯。
package sword_offer; // page 114 打印从1到最大的n位数 public class Solution17 { // 数字排列方法 public static void maxOfND(int n) { if (n < 0) { return; } char[] num = new char[n]; for (int i = 0; i < 10; i++) { num[0] = (char) (i + '0'); printNumRec(num, n, 0); } } // 递归部分 public static void printNumRec(char[] num, int n, int index) { if (index == n - 1) { printNum(num); return; } for (int i = 0; i < 10; i++) { num[index + 1] = (char) (i + '0'); printNumRec(num, n, index + 1); } } // 以阅读习惯输出 public static void printNum(char[] num) { boolean isBegin0 = true; for (int i = 0; i < num.length; i++) { if (isBegin0 && num[i] != '0') { isBegin0 = false; } if (!isBegin0) { System.out.print(num[i]); } } System.out.println(); } // 测试 public static void main(String[] args) { maxOfND(5); } }
面试题18 删除链表的节点
- 描述:在O(1)时间内删除链表节点
- 思路:不直接删除,通过赋值完成。在删除的节点无下一个节点时,则需要从前向后遍历。在删除的节点是头节点时,直接写root = null是无效的,可以考虑写个链表类,包含删除节点的函数。
- 考点:链表具有单方向遍历的性质,但在操作时也要注意技巧。同时要全面考虑。
package sword_offer; // page 119 删除链表中的节点 public class Solution18 { public static void deleteNode(ListNode root, ListNode toBeDeleted) { // 要删的节点是根节点(这种情况下的操作是无效的,没真正删除) if (root.equals(toBeDeleted)) { root = root.next; return; } ListNode tmp = toBeDeleted.next; // 是否是最后一个节点?不是则通过赋值完成删除,是则通过从前向后遍历,完成删除 if (tmp != null) { toBeDeleted.value = tmp.value; if (tmp.next != null) toBeDeleted.next = tmp.next; tmp.next = null; } else { tmp = root; while (!tmp.next.equals(toBeDeleted)) { tmp = tmp.next; } tmp.next = null; } } // 测试 public static void main(String[] args) { ListNode[] ln = new ListNode[6]; // 1 -> 2 -> 3 -> 4 -> 5 -> 6 for (int i = 0; i < ln.length; i++) { ln[i] = new ListNode(); ln[i].value = i; if (i > 0) ln[i - 1].next = ln[i]; } ln[0].printOut(); deleteNode(ln[0], ln[2]); System.out.println("==== after delete ===="); ln[0].printOut(); } }
面试题21 调整数组顺序使奇数位于偶数前面
- 描述:操作输入的整数数组,实现所有奇数位于数组的前部分,偶数位于数组的后部分。
- 思路:比较容易想到使用两个变量分别指向数组的首段、尾端,向中间聚拢,完成数组顺序调整。
- 考点:对数组的操作;对程序扩展性的考虑。
package sword_offer; // page 21 调整数组顺序使奇数位于偶数前面 import java.util.Arrays; public class Solution21 { // 按一定规则调整数组的程序 public static void reorderOddEven(int[] arr) { int start = 0; int end = arr.length - 1; while (start < end) { while (start < end && isOdd(arr[start])) start++; while (start < end && !isOdd(arr[end])) end--; if (start < end) { int tmp = arr[start]; arr[start] = arr[end]; arr[end] = tmp; } } } // 单独定义一个函数,提高扩展性 private static boolean isOdd(int x) { return (x & 1) == 1; } // 测试 public static void main(String[] args) { int[] arr = { 0, 1, 3, 5, 4, 9 }; reorderOddEven(arr); System.out.println(Arrays.toString(arr)); } }
面试题22 链表中的倒数第k个节点
- 描述:输入一个链表,输出链表中倒数第k个节点。
- 思路:无法判断链表大小是主要难点,因此额外定义一个变量,当链表大小大于等于k时进行跟踪。
- 考点:对鲁棒性的考虑;小心处理程序,可避免原文中提到的程序崩溃问题。
package sword_offer; // page 134 链表中倒数第k个节点 /*class ListNode{ Solution6定义过了 ListNode next = null; int value; }*/ public class Solution22 { public static ListNode findKthTail(ListNode head, int k) { ListNode res = head; int i = 1; while (head.next != null) { i++; head = head.next; if (i > k) res = res.next; } if (i < k || k < 1) throw new IllegalArgumentException("Not exist"); return res; } public static void main(String[] args) { ListNode[] ln = new ListNode[6]; // 1 -> 2 -> 3 -> 4 -> 5 -> 6 for (int i = 0; i < ln.length; i++) { ln[i] = new ListNode(); ln[i].value = i + 1; if (i > 0) ln[i - 1].next = ln[i]; } System.out.println(findKthTail(ln[0], 1).value); } }
面试题24 反转链表
- 描述:输入链表的头结点,反转链表并输出反转后链表的头节点。
- 思路:要定义pre和next变量存储断开前后的节点。
- 考点:对链表的理解。
package sword_offer; // page 142 反转链表 public class Solution24 { public static ListNode reverseList(ListNode head) { if (head == null) return null; ListNode pre = null; ListNode next = null; while (head != null) { next = head.next; head.next = pre; pre = head; head = next; } return pre; } // 测试 public static void main(String[] args) { ListNode[] ln = new ListNode[6]; // 1 -> 2 -> 3 -> 4 -> 5 -> 6 for (int i = 0; i < ln.length; i++) { ln[i] = new ListNode(); ln[i].value = i + 1; if (i > 0) ln[i - 1].next = ln[i]; } ln[0].printOut(); reverseList(ln[0]); System.out.println("=========反转前后========"); ln[5].printOut(); } }
面试题25 合并两个排序的链表
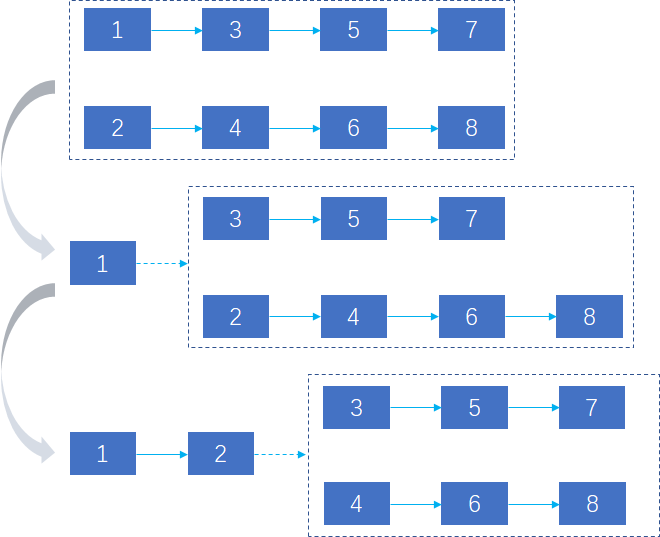
- 描述:输入两个递增排序的链表,合并这两个链表,保证合并后的链表仍是递增的。
- 思路:采用递归的方法,逐次获得下一节点。
- 考点:对问题的分析能力,不使用递归会导致代码不清晰;对链表的理解。
package sword_offer; // page 合并两个排序的链表 public class Solution25 { public static ListNode merge(ListNode head1, ListNode head2) { if (head1 == null) return head2; if (head2 == null) return head1; ListNode mergeHead = null; if (head1.value < head2.value) { mergeHead = head1; mergeHead.next = merge(head1.next, head2); } else { mergeHead = head2; mergeHead.next = merge(head1, head2.next); } return mergeHead; } public static void main(String[] args) { int[] arr1 = { 1, 3, 5, 7 }; int[] arr2 = { 2, 4, 6, 10 }; // 定义链表1 ListNode[] ln1 = new ListNode[arr1.length]; for (int i = 0; i < ln1.length; i++) { ln1[i] = new ListNode(); ln1[i].value = arr1[i]; if (i > 0) ln1[i - 1].next = ln1[i]; } // 定义链表2 ListNode[] ln2 = new ListNode[arr2.length]; for (int i = 0; i < ln1.length; i++) { ln2[i] = new ListNode(); ln2[i].value = arr2[i]; if (i > 0) ln2[i - 1].next = ln2[i]; } merge(ln1[0], ln2[0]).printOut(); } }
面试题27 二叉树的镜像
- 描述:输入一个二叉树,作镜像变换👈👉。
- 思路:即递归交换左右子树。
- 考点:树的遍历算法的熟练掌握,这里用到的是前序遍历。
package sword_offer; // page 157 二叉树的镜像 public class Solution26 { public static void mirrorTree(BinaryTreeNode root) { if (root == null || (root.leftNode == null && root.rightNode == null)) return; BinaryTreeNode tmp = root.leftNode; root.leftNode = root.rightNode; root.rightNode = tmp; if (root.leftNode != null) mirrorTree(root.leftNode); if (root.rightNode != null) mirrorTree(root.rightNode); } // 测试 public static void main(String[] args) { BinaryTreeNode a = new BinaryTreeNode(); BinaryTreeNode b = new BinaryTreeNode(); BinaryTreeNode c = new BinaryTreeNode(); BinaryTreeNode d = new BinaryTreeNode(); BinaryTreeNode e = new BinaryTreeNode(); BinaryTreeNode f = new BinaryTreeNode(); BinaryTreeNode g = new BinaryTreeNode(); a.leftNode = b; a.rightNode = c; b.leftNode = d; b.rightNode = e; c.leftNode = f; c.rightNode = g; a.value = 8; b.value = 6; c.value = 10; d.value = 5; e.value = 7; f.value = 9; g.value = 11; a.printList(); mirrorTree(a); System.out.println("=========="); // 中序输出也是对称的 a.printList(); } }
面试题28 对称的二叉树
- 描述:判断树是不是对称的。
- 思路:书上的分析过程能理解,而要准确无误地写出代码确实另一回事了。这里还是树的遍历。程序可以看成是两个树的比较,更有利于组织清晰的代码。
- 考点:树的遍历。
package sword_offer; // page 159 对称的二叉树 public class Solution28 { public static boolean isSymmetrical(BinaryTreeNode root) { return isSymmetrical(root, root); } private static boolean isSymmetrical(BinaryTreeNode root1, BinaryTreeNode root2) { if (root1 == null && root2 == null) return true; if (root1 == null || root2 == null) return false; if (root1.value != root2.value) return false; return isSymmetrical(root1.leftNode, root2.rightNode) && isSymmetrical(root1.rightNode, root2.leftNode); } // 测试 public static void main(String[] args) { BinaryTreeNode a = new BinaryTreeNode(); BinaryTreeNode b = new BinaryTreeNode(); BinaryTreeNode c = new BinaryTreeNode(); BinaryTreeNode d = new BinaryTreeNode(); BinaryTreeNode e = new BinaryTreeNode(); BinaryTreeNode f = new BinaryTreeNode(); BinaryTreeNode g = new BinaryTreeNode(); a.leftNode = b; a.rightNode = c; b.leftNode = d; b.rightNode = e; c.leftNode = f; c.rightNode = g; a.value = 8; b.value = 6; c.value = 6; d.value = 5; e.value = 7; f.value = 7; g.value = 5; System.out.println(isSymmetrical(a)); } }
面试题32 从上到下打印二叉树
- 描述:从上到下打印二叉树,同一层从左到右打印。
- 思路:需要一个队列。这时应该想到双向链表LinkedList实现了队列、栈。要熟练记住常用的操作。
- 考点:二叉树的前中后遍历输出比较容易处理,而这里要对二叉树和队列有充分的理解才能想到解决方法。
package sword_offer; // page 171 从上到下打印二叉树 import java.util.LinkedList; import java.util.Queue; public class Solution32 { public static void printTreeTopToBottom(BinaryTreeNode root) { if (root == null) return; // 创建个队列queue Queue<BinaryTreeNode> queue = new LinkedList<>(); queue.add(root); while (!queue.isEmpty()) { // 弹出后打印,再插入该节点的左节点、右节点 BinaryTreeNode node = queue.poll(); System.out.println(node.value); if (node.leftNode != null) queue.add(node.leftNode); if (node.rightNode != null) queue.add(node.rightNode); } } // 测试 public static void main(String[] args) { BinaryTreeNode a = new BinaryTreeNode(); BinaryTreeNode b = new BinaryTreeNode(); BinaryTreeNode c = new BinaryTreeNode(); BinaryTreeNode d = new BinaryTreeNode(); BinaryTreeNode e = new BinaryTreeNode(); BinaryTreeNode f = new BinaryTreeNode(); BinaryTreeNode g = new BinaryTreeNode(); a.leftNode = b; a.rightNode = c; b.leftNode = d; b.rightNode = e; c.leftNode = f; c.rightNode = g; a.value = 8; b.value = 6; c.value = 10; d.value = 5; e.value = 7; f.value = 9; g.value = 11; printTreeTopToBottom(a); } }
第5章 优化时间和效率
面试题39 数组中出现次数超过一半的数字
- 描述:数组中有个数字出现的次数超过的数组长度的一半,找出这个数字。
- 思路:1、基于快排的特点(每次确定一个元素的位置),以及排序后的数组中位数位于数组中间位置的特点;2、遍历数组,统计次数。不容易想到。
- 考点:对同类问题的联想能力;对问题的发散思考能力。
package sword_offer; //page 205 数组中出现次数超过一半的数字 public class Solution39 { // 方法1:利用数组中位数的特性以及快速排序的思想 public static int moreThanHalfNum_s1(int[] arr) { int mid = arr.length >> 1; int start = 0; int end = arr.length - 1; int index = partition(arr, start, end); while (index != mid) { if (index > mid) { end = index - 1; index = partition(arr, start, end); } else { start = index + 1; index = partition(arr, start, end); } } int result = arr[mid]; return result; } // 快排确定一个索引 public static int partition(int[] arr, int start, int end) { int mid = end; end = end - 1; while (start < end) { while (start < end && arr[start] < arr[mid]) start++; while (start < end && arr[end] >= arr[mid]) end--; swap(arr, start, end); } if (arr[start] >= arr[mid]) { swap(arr, start, mid); } else start++; return start; } // 交换 private static void swap(int[] arr, int x, int y) { int temp = arr[x]; arr[x] = arr[y]; arr[y] = temp; } // 方法2:基于数组特点 public static int moreThanHalfNum_s2(int[] arr) { int result = arr[0]; int times = 1; for (int i = 1; i < arr.length; i++) { if (times == 0) { result = arr[i]; times = 1; } else if (arr[i] == result) times++; else times--; } return result; } // 测试 public static void main(String[] args) { int[] arr = { 3, 3, 1, 1, 1, 4, 4, 1 }; System.out.println(moreThanHalfNum_s1(arr)); System.out.println(moreThanHalfNum_s2(arr)); } }
面试题40 最小的k个数
- 描述:输入n个整数,找出其中最小的k个数。
- 思路:基于快排的特点,容易实现数组元素大小的查找。同理也很容易找到第k大的数,别忘了容易犯的差1错误。
- 考点:对同类问题的联想能力。
package sword_offer; // page 209 最小的k个数 import java.util.Arrays; public class Solution40 { public static void getLeastNums(int[] arr, int k) { int start = 0; int end = arr.length - 1; int index = partition(arr, start, end); while (index != k - 1) { // 注意索引与个数的关系,注意差1错误 if (index < k - 1) { start = index + 1; index = partition(arr, start, end); } else { end = index - 1; index = partition(arr, start, end); } } } // 快排确定一个索引 public static int partition(int[] arr, int start, int end) { int mid = end; end = end - 1; while (start < end) { while (start < end && arr[start] < arr[mid]) start++; while (start < end && arr[end] >= arr[mid]) end--; swap(arr, start, end); } if (arr[start] >= arr[mid]) { swap(arr, start, mid); } else start++; return start; } // 交换 private static void swap(int[] arr, int x, int y) { int temp = arr[x]; arr[x] = arr[y]; arr[y] = temp; } // 测试 public static void main(String[] args) { int[] arr = { 3, 3, 1, 1, 1, 4, 4, 1 }; getLeastNums(arr, 1); System.out.println(Arrays.toString(arr)); } }
面试题42 连续子数组的最大和
- 描述:输入一个整形数组,元素有正有负。求子数组的和的最大值。要求时间复杂度为O(n)。
- 思路:累加数组,存储临时变量,一旦该量为负则置0,一旦该量大于累加值,则赋为累加值。
- 考点:这道题挺有名的,编程珠玑这本书又讲到,也算是考察了历史了。没见过这道题却能想出来O(n)算法的肯定很厉害。
package sword_offer; // page 218 连续子数组的最大和 public class Solution42 { public static int maxSub(int[] arr) { int maxSum = 0, tempSum = 0; for (int i = 0; i < arr.length; i++) { tempSum += arr[i]; if (tempSum > maxSum) maxSum = tempSum; else if (tempSum < 0) tempSum = 0; } return maxSum; } // 测试 public static void main(String[] args) { int[] arr = { 1, -2, 3, 10, -4, 7, 2, -5 }; System.out.println(maxSub(arr)); } }
面试题43 1~n整数中出现1的个数
- 描述:输入一个整数n,求1~n这n个整数的十进制表示中出现1的次数。
- 思路:很容易想到nlog(n)的算法,即对10求余。log(n)的方法不易想到,后面再更。
- 考点:一般的方法大部分都能想到,但更好的方法则需要优化的激情和一定的思维能力。
package sword_offer; // page 221 1~n整数中出现1的个数 public class Solution43 { // 计算整数n中含有1的个数 private static int countOne(int n) { int count = 0; while (n != 0) { if (n % 10 == 1) count++; n = n / 10; } return count; } // 计算整数1~n中含有1的个数 public static int countTotalOne(int n) { int count = 0; for (int i = 1; i <= n; i++) { count += countOne(i); } return count; } // 测试 public static void main(String[] args) { System.out.println(countTotalOne(100)); } }
面试题44 数字序列中的某一位的数
- 描述:数字以012345678910111213141516...的格式化序列排列。从0开始计数:第0位是0,第5位是5,第10位是1...。写个函数,求任意n位对应的数字。
- 思路:找规律。发现找规律的题目并不容易写对,总是在临界处出现差1错误,而且差1问题很容易让人卡壳;或者规律找到了,但思路很乱的,写的代码调了半天也能运行,但结构不清晰。
- 考点:对数字规律的总结能力。
package sword_offer; // page 225 数组序列中的某一位数字 import java.lang.Math; public class Solution44 { // 这里没采用原文中将程序拆分为几个小程序的形式,考虑到个位数的特殊性,直接在前面处理 public static int digitAtIndex(int index) { if (index < 10) return index; int n = 2; //位数 index = index - 10;//初始化位位数为1的个数 while(true) { int numsOfN = 9 * (int) Math.pow(10, n - 1); //n位的个数 if (index < numsOfN * n) { //是否在这个区间 int number = (int) Math.pow(10, n - 1) + index / n; //对应的整数 int indexFromRight = n - index % n; //从右边数第几位 for (int i = 1; i < indexFromRight; i++) { //找到那一位 number /= 10; } return number % 10; } index -= numsOfN * n; n++; } } // 测试 public static void main(String[] args) { System.out.println(digitAtIndex(1001)); } }
面试题45 把数组排列成最小的数
- 描述:输入一个正整数数组,把数组中的所有数字拼接排成一个数,打印出最小的那个数。
- 思路:字符串表示大数+快速排序+字符串大小比较。
- 考点:算是对综合能力的考察。拼接的数很容易溢出,因此可以用字符串表示大数;考查了对于字符串的处理能力,在比较字符串mn大还是nm大时,可以逐位转化比较或者直接用Sting对象的compareTo方法。要能快速、正确地写出快排算法,好几道题都用到了。
package sword_offer; // page 227 把数组排成最小的数 public class Solution45 { public static void printMin(int[] arr) { printMinNumber(arr, 0, arr.length - 1); for (int i : arr) System.out.print(i); System.out.println(); } // 注意快排的不同形式 public static void printMinNumber(int[] arr, int left, int right) { if (left < right) { int main_number = arr[right]; int small_cur = left; for (int j = left; j < right; j++) { if (isSmall(String.valueOf(arr[j]), String.valueOf(main_number))) { // 小于时交换 int temp = arr[j]; arr[j] = arr[small_cur]; arr[small_cur] = temp; small_cur++; } } arr[right] = arr[small_cur]; arr[small_cur] = main_number; printMinNumber(arr, 0, small_cur - 1); printMinNumber(arr, small_cur + 1, right); } } // 判断字符串是否满足mn < nm public static boolean isSmall(String m, String n) { String left = m + n; String right = n + m; return left.compareTo(right) < 0; // 也可以重写函数 } // 测试 public static void main(String[] args) { int arr[] = { 3, 1, 2, 11 }; printMin(arr); } }
面试题49 丑数
- 描述:将只包含2、3、5的数称为丑数。求从小到大的第1500个丑数。第一个丑数定为1。
- 思路:第1种方法按个判断是否是丑数;第二种算法使用了额外空间换得了效率。1500个整形数约占内存6KB,但换来了千倍的加速。在面试时可以和面试官交流能否使用辅助空间。
- 考点:对新概念的理解能力;对编写高效程序的能力。

package sword_offer; // page 240 丑数 public class Solution49 { // 方法1:一个一个判断是否是丑数,直到找到目标值 public static int getUglyNum_s1(int index) { int count = 0; int num = 0; while (count < index) { num++; // 把num++放在循环的开头而非末尾 if (isUglyNum(num)) count++; } return num; } // 判断是否是丑数 private static boolean isUglyNum(int n) { while (n % 2 == 0) n /= 2; while (n % 3 == 0) n /= 3; while (n % 5 == 0) n /= 5; return n == 1 ? true : false; } // 方法2:额外定义个缓存数组,将丑数存下来,注意里面使用3个变量跟踪的技巧 public static int getUglyNum_s2(int index) { int[] uglyNums = new int[index]; uglyNums[0] = 1; int pm2 = 0; int pm3 = 0; int pm5 = 0; int nextIndex = 1; while (nextIndex < index) { int min = minNum(uglyNums[pm2] * 2, uglyNums[pm3] * 3, uglyNums[pm5] * 5); uglyNums[nextIndex] = min; while (uglyNums[pm2] * 2 <= min) pm2++; while (uglyNums[pm3] * 3 <= min) pm3++; while (uglyNums[pm5] * 5 <= min) pm5++; nextIndex++; // 这里将nextIndex++放到末尾,因为是索引 } return uglyNums[nextIndex - 1]; } // 三个数中的最小值 public static int minNum(int x, int y, int z) { int min = x < y ? x : y; min = z < min ? z : min; return min; } // 测试 public static void main(String[] args) { long t0 = System.currentTimeMillis(); System.out.println("方法1计算的第1500个丑数:" + getUglyNum_s1(1500)); long t1 = System.currentTimeMillis(); System.out.println("方法1耗时:" + (t1 - t0) + "ms"); System.out.println("方法2计算的第1500个丑数:" + getUglyNum_s2(1500)); long t2 = System.currentTimeMillis(); System.out.println("方法2耗时:" +(t2 - t1) + "ms"); } }
面试题50 第一个只出现一次的字符
- 描述:字符串中第一个只出现一次的字符。
- 思路:利用字符的ASCII作为数组的索引,实现一个简单的哈希表。先遍历字符串计数,再遍历数组。
- 考点:对字符串以及哈希表的理解。
package sword_offer; // 第一个只出现一次的字符 public class Solution50 { // 将ASCII作为数组下标,存储出现的个数,相当于实现了一个简单的哈希表,也可以直接用map public static char firstRepeatchar(String str) { int maxNum = 256; char target = str.charAt(0); int[] arr = new int[maxNum]; for (int i = 0; i < str.length(); i++) arr[(int)(str.charAt(i))]++; for (int i = 0; i < str.length(); i++) { if (arr[(int)(str.charAt(i))] == 1){ target = str.charAt(i); break; } } return target; } // 相关题目:删除重复的字符 public static String delRepeatchar(String str) { int maxNum = 256; StringBuilder strb = new StringBuilder(); int[] arr = new int[maxNum]; for (int i = 0; i < str.length(); i++) { if (arr[(int)(str.charAt(i))] == 0) { arr[(int)(str.charAt(i))]++; strb.append(str.charAt(i)); } } return strb.toString(); } // 相关题目:从第一个字符串中删除在第二个字符串中出现过的所有字符 public static String delCharInStr2(String str1, String str2) { int maxNum = 256; StringBuilder strb = new StringBuilder(); int[] arr = new int[maxNum]; for (int i = 0; i < str2.length(); i++) { if (arr[(int)(str2.charAt(i))] == 0) { arr[(int)(str2.charAt(i))]++; } } for (int i = 0; i < str1.length(); i++) { if (arr[(int)(str1.charAt(i))] == 0) { // str1中的字符对应的哈希表在arr中不存在 strb.append(str1.charAt(i)); } } return strb.toString(); } // 相关题目:判断是否是变位词 public static boolean isAnagram(String str1, String str2) { int maxNum = 256; int[] arr = new int[maxNum]; if (str1.length() != str2.length()) return false; for (int i = 0; i < str1.length(); i++) { arr[(int)(str1.charAt(i))]++; arr[(int)(str2.charAt(i))]--; } for (int i = 0; i < arr.length; i++) { if (arr[i] != 0) return false; } return true; } // 测试 public static void main(String[] args) { System.out.println(firstRepeatchar("abaccdeff")); System.out.println(delRepeatchar("abaccdeff")); System.out.println(delCharInStr2("We are student.", "aeiou")); System.out.println(isAnagram("silent", "listen")); } }
面试题55 二叉树的深度
- 描述:输入二叉树的根节点,求数的深度。
- 思路:利用递归求解:左子树、右子树中深度大者加一。
- 考点:对树深度的理解,构建递归算法。
package sword_offer; // page 271 二叉树的深度 public class Solution55 { public static int treeDepth(BinaryTreeNode root) { // 基准情况 if (root == null) return 0; // 左子树深度 int nleft = treeDepth(root.leftNode); // 右子树深度 int nright = treeDepth(root.rightNode); return (nleft > nright) ? nleft + 1 : nright + 1; } // 测试 public static void main(String[] args) { BinaryTreeNode a = new BinaryTreeNode(); BinaryTreeNode b = new BinaryTreeNode(); BinaryTreeNode c = new BinaryTreeNode(); a.rightNode = b; b.leftNode = c; System.out.println(treeDepth(a)); } }
第6章 面试中的各项能力
面试题64 求1+2+...+n
- 描述:求1+2+...+n,要求不能使用乘除、for、while、if、else、switch、case等关键字和条件判断语句。
- 思路:像这样的题目本身无太大实际意义,少做这种题。这里可以利用与、或逻辑运算的性质,想到才能做出来。貌似不能用递归,但还是用了递归,不过不用if来终止罢了。
- 考点:对怪问题的把握能力。
package sword_offer; // page 307 求1+2+...+n public class Solution64 { public static int sum1(int n) { // 利用与运算的性质,实现了递归的终止 boolean flag = (n > 0) && (n = n + sum1(n - 1)) > 0; // (n == 0) || (n = n + sum1(n - 1)) > 0; return n; } // 测试 public static void main(String[] args) { System.out.println(sum1(2)); } }





