matmul优化
HOW TO OPTIMIZE GEMM
介绍一些常规的优化思路,参考:https://github.com/flame/how-to-optimize-gemm/wiki
baseline
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j, p; for ( i=0; i<m; i++ ){ /* Loop over the rows of C */ for ( j=0; j<n; j++ ){ /* Loop over the columns of C */ for ( p=0; p<k; p++ ){ /* Update C( i,j ) with the inner product of the ith row of A and the jth column of B */ C( i,j ) = C( i,j ) + A( i,p ) * B( p,j ); } } } }
这是代数逻辑的实现。三个矩阵都是以列主序存储的。
opt1
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot( int, double *, int, double *, double * ); void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=1 ){ /* Loop over the columns of C */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update the C( i,j ) with the inner product of the ith row of A and the jth column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) ); } } } /* Create macro to let X( i ) equal the ith element of x */ #define X(i) x[ (i)*incx ] void AddDot( int k, double *x, int incx, double *y, double *gamma ) { /* compute gamma := x' * y + gamma with vectors x and y of length n. Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1. */ int p; for ( p=0; p<k; p++ ){ *gamma += X( p ) * y[ p ]; } }
A的ith行,B的jth列。
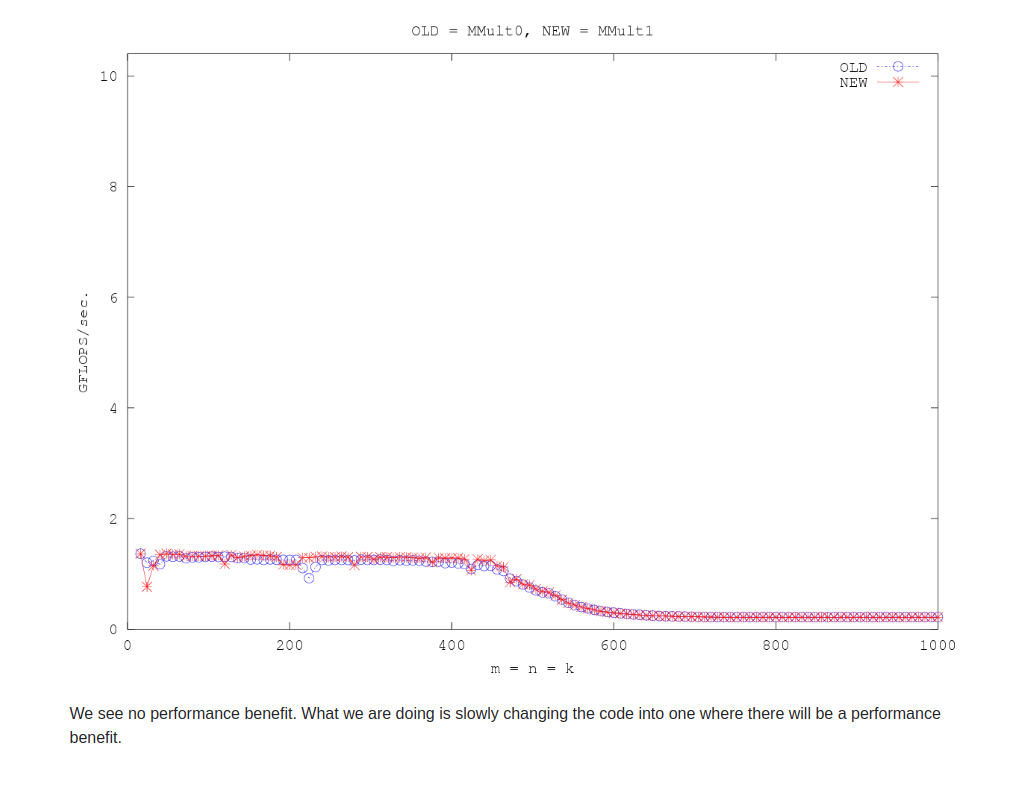
没有更改计算模式,还增加了调用开销。
opt2
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot( int, double *, int, double *, double * ); void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update the C( i,j ) with the inner product of the ith row of A and the jth column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j ), &C( i,j ) ); /* Update the C( i,j+1 ) with the inner product of the ith row of A and the (j+1)th column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j+1 ), &C( i,j+1 ) ); /* Update the C( i,j+2 ) with the inner product of the ith row of A and the (j+2)th column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j+2 ), &C( i,j+2 ) ); /* Update the C( i,j+3 ) with the inner product of the ith row of A and the (j+1)th column of B */ AddDot( k, &A( i,0 ), lda, &B( 0,j+3 ), &C( i,j+3 ) ); } } } /* Create macro to let X( i ) equal the ith element of x */ #define X(i) x[ (i)*incx ] void AddDot( int k, double *x, int incx, double *y, double *gamma ) { /* compute gamma := x' * y + gamma with vectors x and y of length n. Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1. */ int p; for ( p=0; p<k; p++ ){ *gamma += X( p ) * y[ p ]; } }
这里做了循环展开,B的jth列unroll 4。
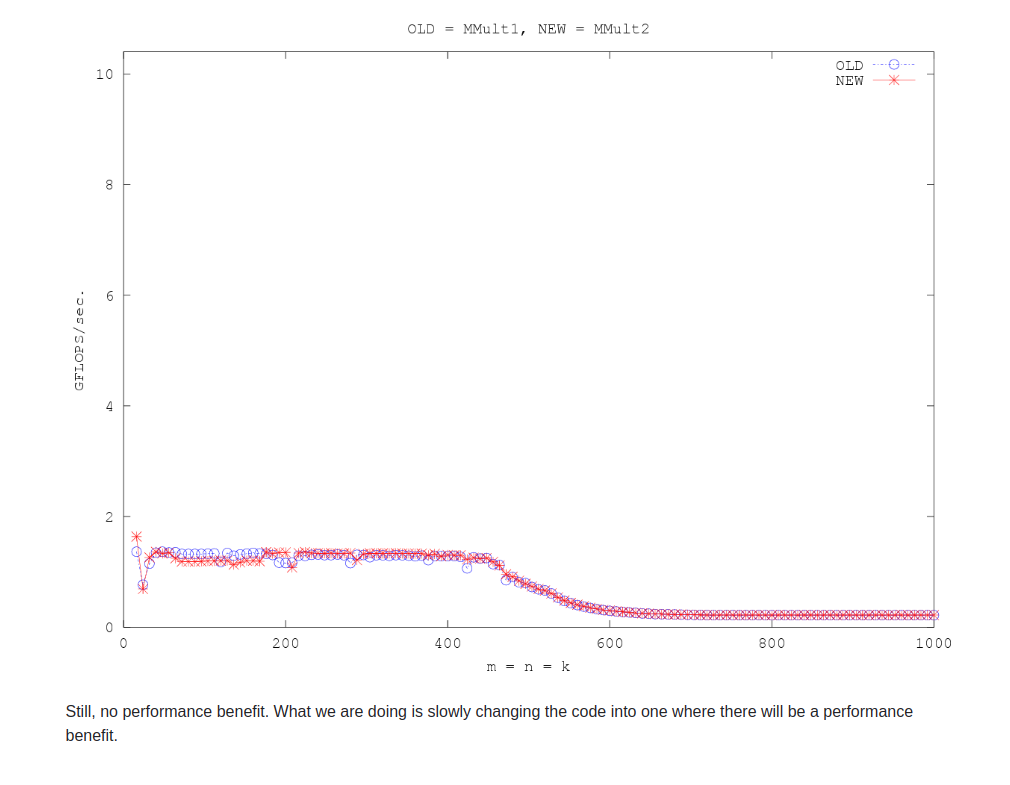
opt3
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot( int, double *, int, double *, double * ); void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C */ AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) ); AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) ); AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) ); AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) ); } /* Create macro to let X( i ) equal the ith element of x */ #define X(i) x[ (i)*incx ] void AddDot( int k, double *x, int incx, double *y, double *gamma ) { /* compute gamma := x' * y + gamma with vectors x and y of length n. Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1. */ int p; for ( p=0; p<k; p++ ){ *gamma += X( p ) * y[ p ]; } }
仍然是jth列unroll 4
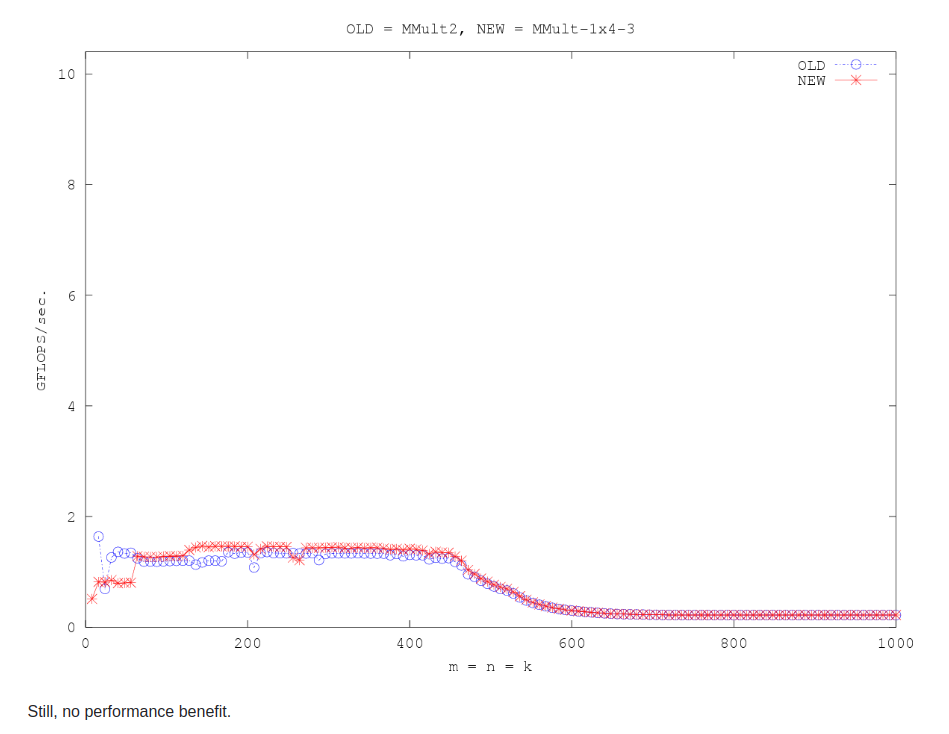
opt4
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C. In this version, we "inline" AddDot */ int p; // AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) ); for ( p=0; p<k; p++ ){ C( 0, 0 ) += A( 0, p ) * B( p, 0 ); } // AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) ); for ( p=0; p<k; p++ ){ C( 0, 1 ) += A( 0, p ) * B( p, 1 ); } // AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) ); for ( p=0; p<k; p++ ){ C( 0, 2 ) += A( 0, p ) * B( p, 2 ); } // AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) ); for ( p=0; p<k; p++ ){ C( 0, 3 ) += A( 0, p ) * B( p, 3 ); } }
仍然是unroll的思路,没有本质区别。
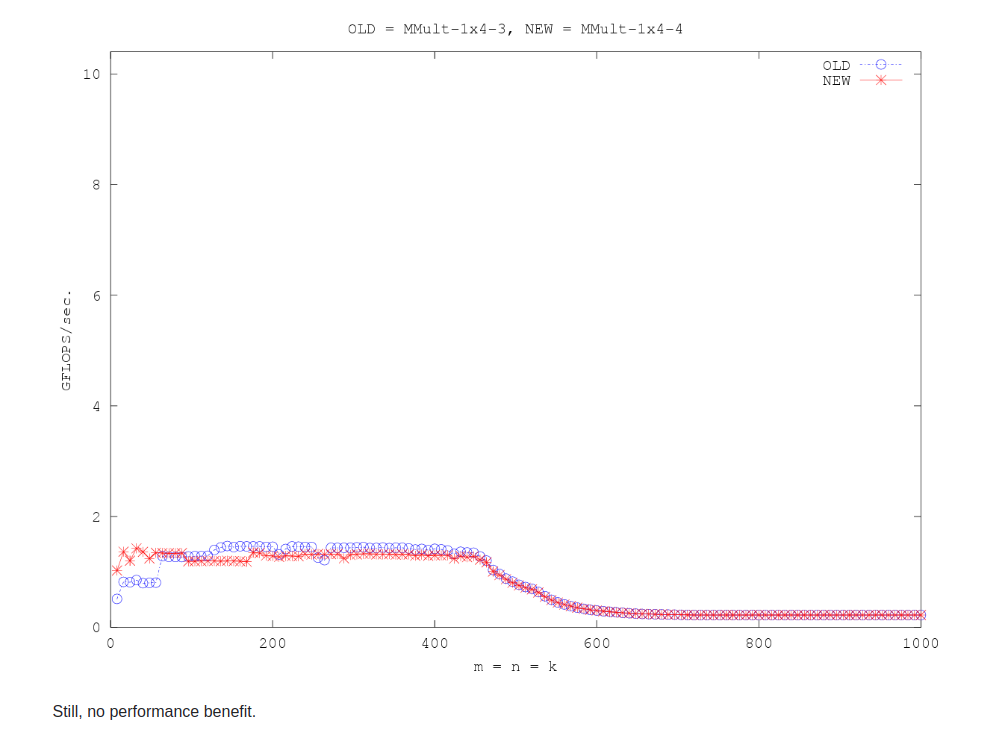
opt5
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C. In this version, we merge the four loops, computing four inner products simultaneously. */ int p; // AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) ); // AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) ); // AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) ); // AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) ); for ( p=0; p<k; p++ ){ C( 0, 0 ) += A( 0, p ) * B( p, 0 ); C( 0, 1 ) += A( 0, p ) * B( p, 1 ); C( 0, 2 ) += A( 0, p ) * B( p, 2 ); C( 0, 3 ) += A( 0, p ) * B( p, 3 ); } }
这里是真正有效的unroll4;与之前的实现相比,A的访存次数减少为1/4(之前的unroll实现中,A的一行要反复读4次,现在只读一次)
此外,A行中的每一个元素与B中unroll列的元素相乘。总体上计算逻辑仍然是代数的,但是在一个iter中拿A中的一个元素做了四次乘法。
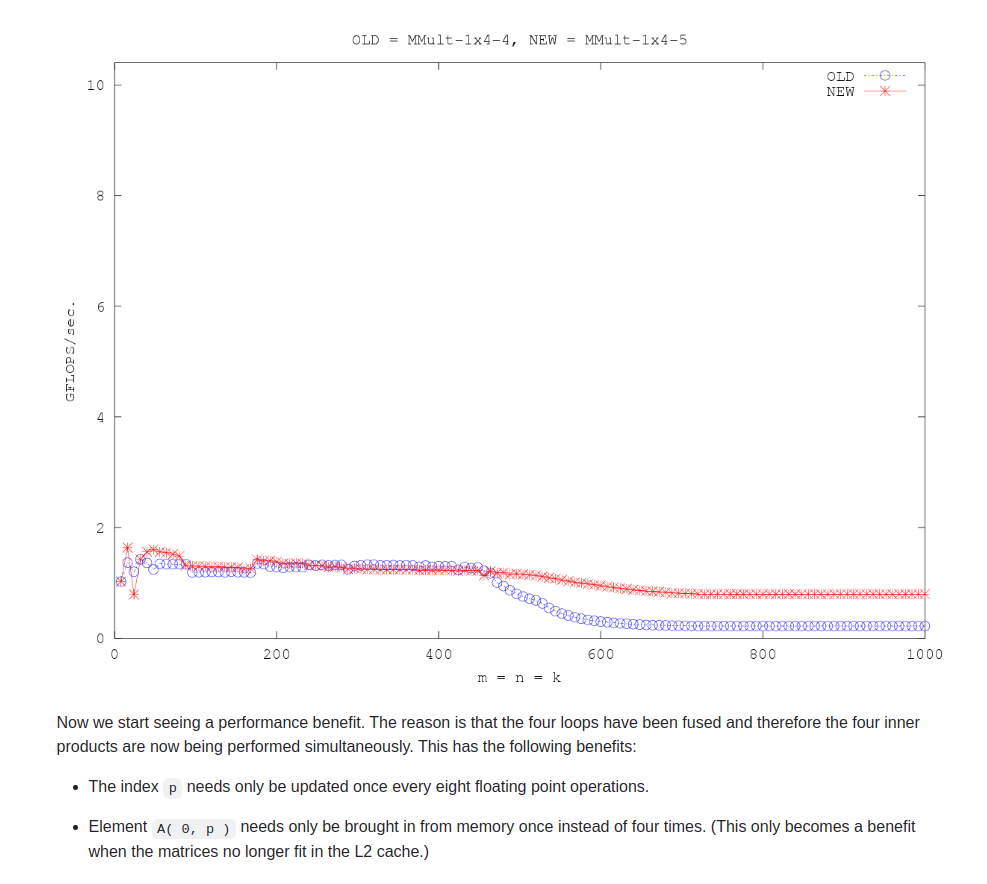
opt6
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C. In this version, we accumulate in registers and put A( 0, p ) in a register */ int p; register double /* hold contributions to C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */ c_00_reg, c_01_reg, c_02_reg, c_03_reg, /* holds A( 0, p ) */ a_0p_reg; c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0; for ( p=0; p<k; p++ ){ a_0p_reg = A( 0, p ); c_00_reg += a_0p_reg * B( p, 0 ); c_01_reg += a_0p_reg * B( p, 1 ); c_02_reg += a_0p_reg * B( p, 2 ); c_03_reg += a_0p_reg * B( p, 3 ); } C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg; }
之前的实现中,C的这四个位置分别访存k次。A的一行中每个元素访存4次。B的4列,分别访存p次。
for ( p=0; p<k; p++ ){
C( 0, 0 ) += A( 0, p ) * B( p, 0 );
C( 0, 1 ) += A( 0, p ) * B( p, 1 );
C( 0, 2 ) += A( 0, p ) * B( p, 2 );
C( 0, 3 ) += A( 0, p ) * B( p, 3 );
}
现在,A的一行总访存1次,预期减少为1/4。B的访存没有变化。C的四个位置分别访存一次。
宏观上,A和C的访存次数分别减少为原来的1/4。
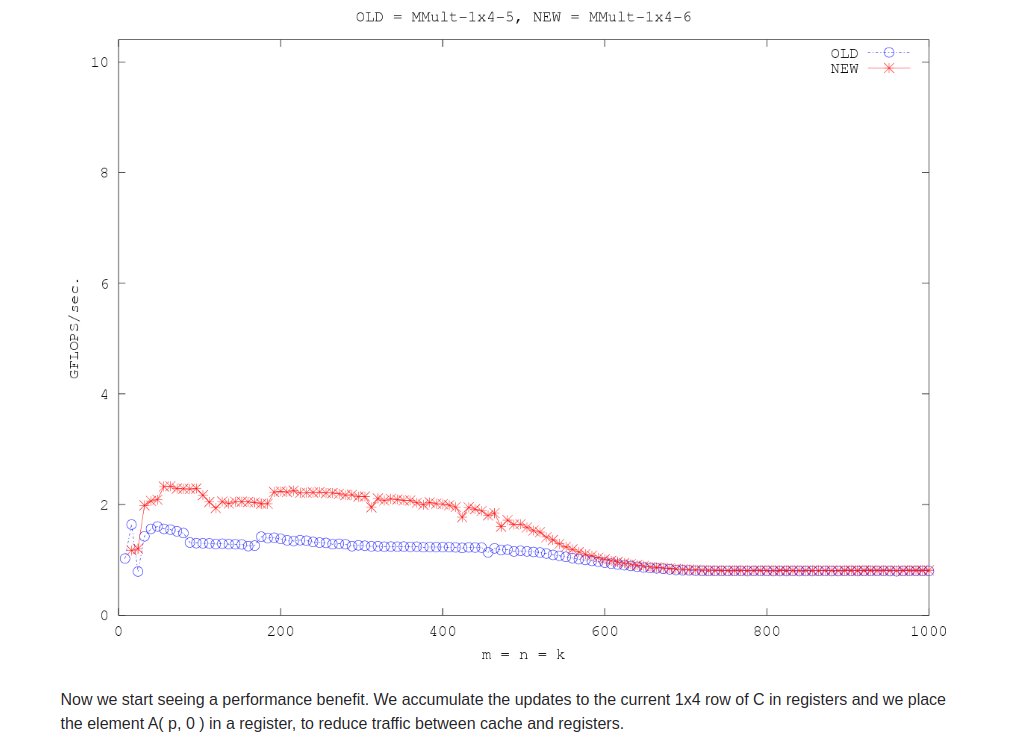
减少了访存请求,也就减少了访问cache的开销。
opt7
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C. In this version, we use pointer to track where in four columns of B we are */ int p; register double /* hold contributions to C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */ c_00_reg, c_01_reg, c_02_reg, c_03_reg, /* holds A( 0, p ) */ a_0p_reg; double /* Point to the current elements in the four columns of B */ *bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr; bp0_pntr = &B( 0, 0 ); bp1_pntr = &B( 0, 1 ); bp2_pntr = &B( 0, 2 ); bp3_pntr = &B( 0, 3 ); c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0; for ( p=0; p<k; p++ ){ a_0p_reg = A( 0, p ); c_00_reg += a_0p_reg * *bp0_pntr++; c_01_reg += a_0p_reg * *bp1_pntr++; c_02_reg += a_0p_reg * *bp2_pntr++; c_03_reg += a_0p_reg * *bp3_pntr++; } C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg; }
相比像一个optimization,只是在B的访存时,减少了索引的逻辑运算,即减少了一些偏移的数学运算。影响太小了,估计没有变化。
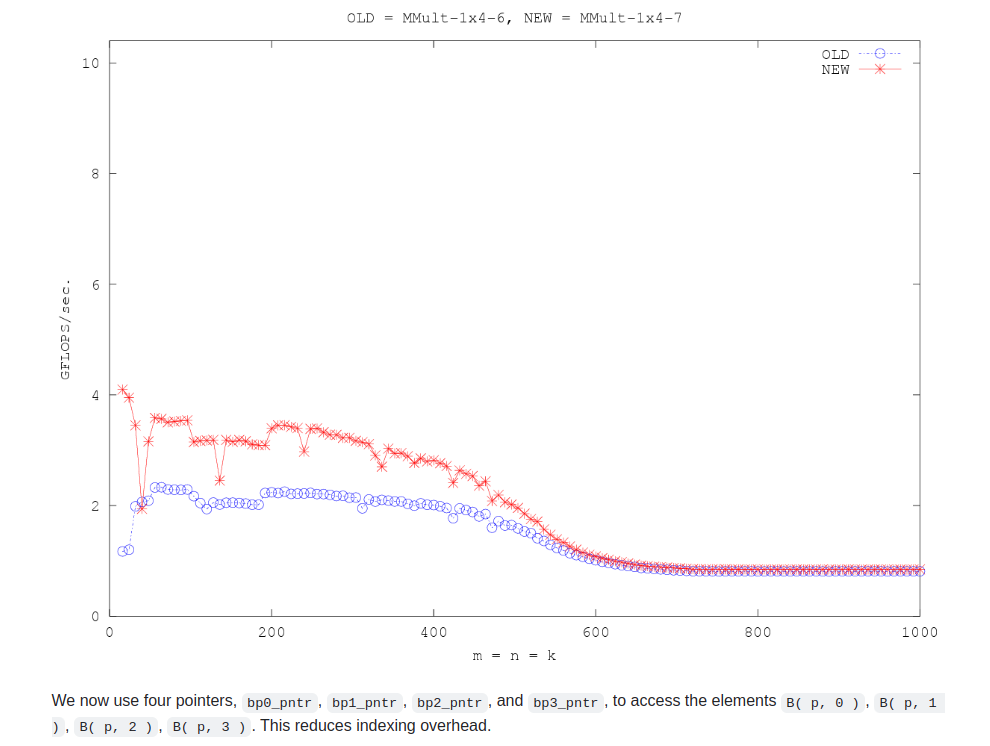
颇为震惊,在problemsize<500时,居然带来如此大收益
如果矩阵乘法的计算强度足够高(即计算量相对于内存访问量来说很大),则减少索引计算的开销可能对总体性能的提升不是非常明显。另一方面,如果处理器的内存访问延迟较高,且编译器没有有效地优化索引计算,那么版本B中的优化可能会带来比较明显的性能提升。
当内存访问延迟高时,导致处理器等待数据时,主要问题是处理器的计算单元不能执行有意义的工作,因为它们正在等待数据到达。在这种情况下,优化内存访问模式和减少索引计算的开销并不能直接减少等待内存数据的时间。
然而,通过优化索引计算和内存访问模式,可以在处理器等待内存数据的同时,尽可能有效地利用可用的计算资源。具体来说:
- 提高计算与内存访问的重叠 :在许多处理器架构中,可以同时进行计算和内存访问。通过减少对索引计算的开销,可以在数据到达之前或之后更快地完成更多的计算工作。这意味着在等待内存数据时,处理器可以完成更多其他不依赖于这些特定内存数据的计算任务。
- 提高计算密集度 :通过减少索引计算的开销,程序可以更多地专注于实际的数值计算,从而提高程序的计算密集度。这有助于在数据到达后立即利用这些数据进行计算,减少处理器空闲时间。
- 优化内存访问模式 :优化内存访问模式(例如,通过使用指针访问连续的内存位置)可以改善缓存的利用率,从而减少未来内存访问的延迟。虽然这不会减少当前正在等待的内存访问的延迟,但它可以减少后续内存访问的潜在延迟,从而在整体上提高程序的执行效率。
综上所述,减少索引计算的开销和优化内存访问模式并不能直接减少因内存访问延迟导致的等待时间,但它们可以使处理器在等待内存数据期间和数据到达后更有效地利用计算资源,从而间接提高程序的总体性能。
opt8
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C. We now unroll the loop */ int p; register double /* hold contributions to C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */ c_00_reg, c_01_reg, c_02_reg, c_03_reg, /* holds A( 0, p ) */ a_0p_reg; double /* Point to the current elements in the four columns of B */ *bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr; bp0_pntr = &B( 0, 0 ); bp1_pntr = &B( 0, 1 ); bp2_pntr = &B( 0, 2 ); bp3_pntr = &B( 0, 3 ); c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0; for ( p=0; p<k; p+=4 ){ a_0p_reg = A( 0, p ); c_00_reg += a_0p_reg * *bp0_pntr++; c_01_reg += a_0p_reg * *bp1_pntr++; c_02_reg += a_0p_reg * *bp2_pntr++; c_03_reg += a_0p_reg * *bp3_pntr++; a_0p_reg = A( 0, p+1 ); c_00_reg += a_0p_reg * *bp0_pntr++; c_01_reg += a_0p_reg * *bp1_pntr++; c_02_reg += a_0p_reg * *bp2_pntr++; c_03_reg += a_0p_reg * *bp3_pntr++; a_0p_reg = A( 0, p+2 ); c_00_reg += a_0p_reg * *bp0_pntr++; c_01_reg += a_0p_reg * *bp1_pntr++; c_02_reg += a_0p_reg * *bp2_pntr++; c_03_reg += a_0p_reg * *bp3_pntr++; a_0p_reg = A( 0, p+3 ); c_00_reg += a_0p_reg * *bp0_pntr++; c_01_reg += a_0p_reg * *bp1_pntr++; c_02_reg += a_0p_reg * *bp2_pntr++; c_03_reg += a_0p_reg * *bp3_pntr++; } C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg; }
A也unroll 4,逻辑上仍然是代数matmul
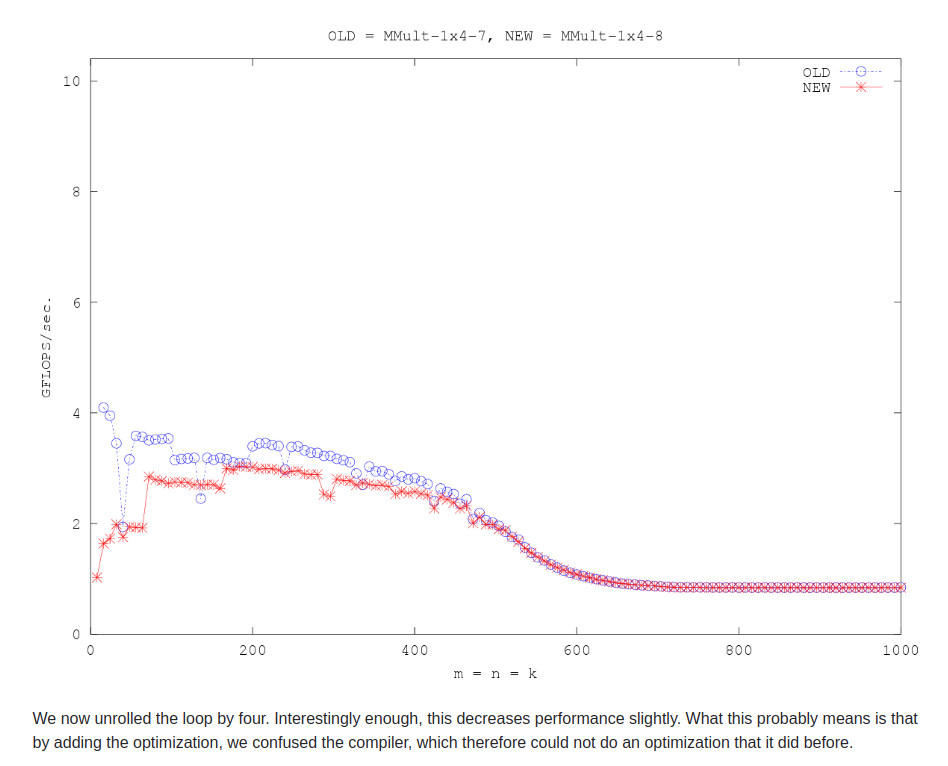
opt9
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot1x4( int, double *, int, double *, int, double *, int ) void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=1 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot1x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot1x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes four elements of C: C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i, j ), C( i, j+1 ), C( i, j+2 ), C( i, j+3 ) in the original matrix C. We next use indirect addressing */ int p; register double /* hold contributions to C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) */ c_00_reg, c_01_reg, c_02_reg, c_03_reg, /* holds A( 0, p ) */ a_0p_reg; double /* Point to the current elements in the four columns of B */ *bp0_pntr, *bp1_pntr, *bp2_pntr, *bp3_pntr; bp0_pntr = &B( 0, 0 ); bp1_pntr = &B( 0, 1 ); bp2_pntr = &B( 0, 2 ); bp3_pntr = &B( 0, 3 ); c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0; for ( p=0; p<k; p+=4 ){ a_0p_reg = A( 0, p ); c_00_reg += a_0p_reg * *bp0_pntr; c_01_reg += a_0p_reg * *bp1_pntr; c_02_reg += a_0p_reg * *bp2_pntr; c_03_reg += a_0p_reg * *bp3_pntr; a_0p_reg = A( 0, p+1 ); c_00_reg += a_0p_reg * *(bp0_pntr+1); c_01_reg += a_0p_reg * *(bp1_pntr+1); c_02_reg += a_0p_reg * *(bp2_pntr+1); c_03_reg += a_0p_reg * *(bp3_pntr+1); a_0p_reg = A( 0, p+2 ); c_00_reg += a_0p_reg * *(bp0_pntr+2); c_01_reg += a_0p_reg * *(bp1_pntr+2); c_02_reg += a_0p_reg * *(bp2_pntr+2); c_03_reg += a_0p_reg * *(bp3_pntr+2); a_0p_reg = A( 0, p+3 ); c_00_reg += a_0p_reg * *(bp0_pntr+3); c_01_reg += a_0p_reg * *(bp1_pntr+3); c_02_reg += a_0p_reg * *(bp2_pntr+3); c_03_reg += a_0p_reg * *(bp3_pntr+3); bp0_pntr+=4; bp1_pntr+=4; bp2_pntr+=4; bp3_pntr+=4; } C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg; }
这里与opt8差不多,但仍然比opt7差。
作者说,这个opt9的目的是减少指针的更新次数。结果是收效不大。
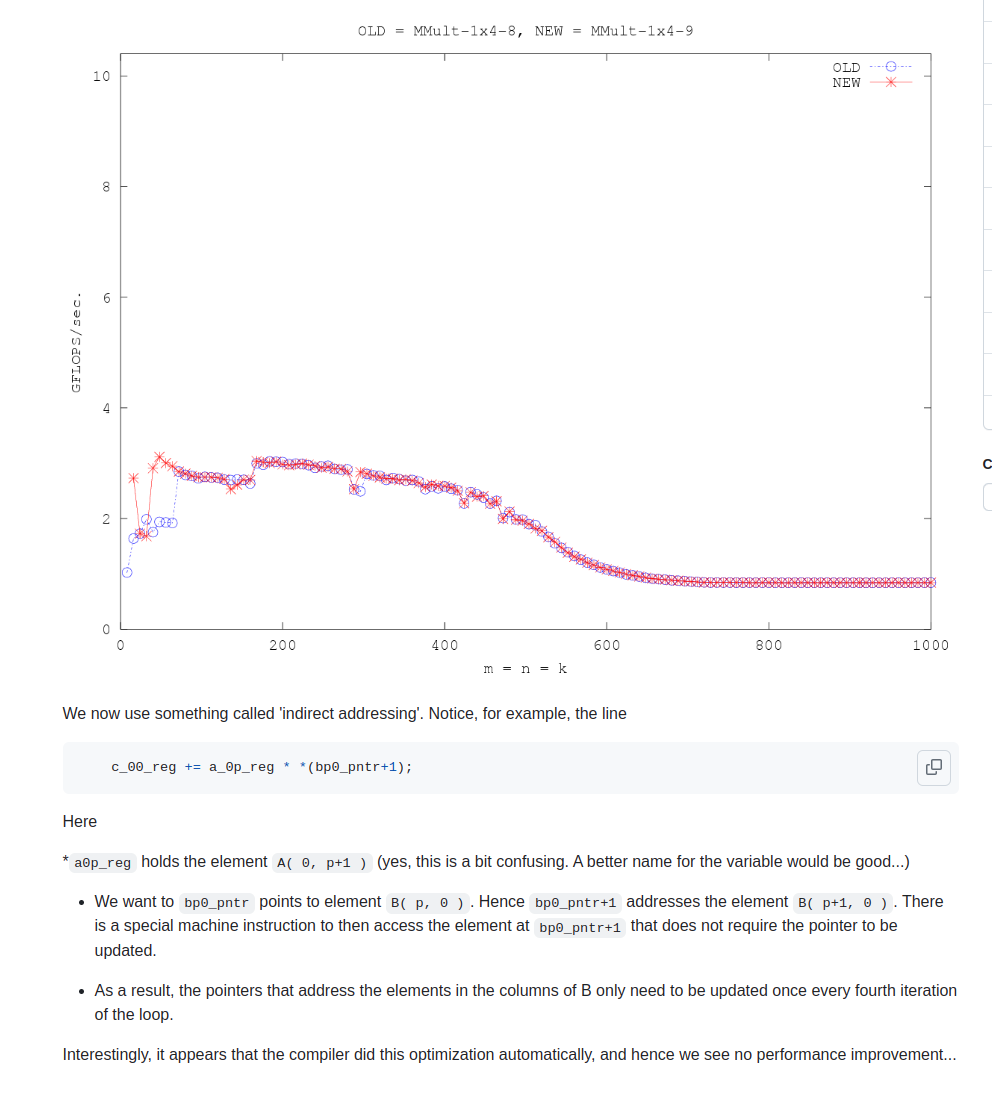
opt10
改为4x4
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot( int, double *, int, double *, double * ); void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=4 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot4x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes a 4x4 block of matrix A C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ). C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ). C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i , j ), C( i , j+1 ), C( i , j+2 ), C( i , j+3 ) C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) in the original matrix C */ /* First row */ AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) ); AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) ); AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) ); AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) ); /* Second row */ AddDot( k, &A( 1, 0 ), lda, &B( 0, 0 ), &C( 1, 0 ) ); AddDot( k, &A( 1, 0 ), lda, &B( 0, 1 ), &C( 1, 1 ) ); AddDot( k, &A( 1, 0 ), lda, &B( 0, 2 ), &C( 1, 2 ) ); AddDot( k, &A( 1, 0 ), lda, &B( 0, 3 ), &C( 1, 3 ) ); /* Third row */ AddDot( k, &A( 2, 0 ), lda, &B( 0, 0 ), &C( 2, 0 ) ); AddDot( k, &A( 2, 0 ), lda, &B( 0, 1 ), &C( 2, 1 ) ); AddDot( k, &A( 2, 0 ), lda, &B( 0, 2 ), &C( 2, 2 ) ); AddDot( k, &A( 2, 0 ), lda, &B( 0, 3 ), &C( 2, 3 ) ); /* Four row */ AddDot( k, &A( 3, 0 ), lda, &B( 0, 0 ), &C( 3, 0 ) ); AddDot( k, &A( 3, 0 ), lda, &B( 0, 1 ), &C( 3, 1 ) ); AddDot( k, &A( 3, 0 ), lda, &B( 0, 2 ), &C( 3, 2 ) ); AddDot( k, &A( 3, 0 ), lda, &B( 0, 3 ), &C( 3, 3 ) ); } /* Create macro to let X( i ) equal the ith element of x */ #define X(i) x[ (i)*incx ] void AddDot( int k, double *x, int incx, double *y, double *gamma ) { /* compute gamma := x' * y + gamma with vectors x and y of length n. Here x starts at location x with increment (stride) incx and y starts at location y and has (implicit) stride of 1. */ int p; for ( p=0; p<k; p++ ){ *gamma += X( p ) * y[ p ]; } }
Aunroll4,没有提高
opt11
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot4x4( int, double *, int, double *, int, double *, int ); void AddDot( int, double *, int, double *, double * ); void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=4 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot4x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes a 4x4 block of matrix A C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ). C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ). C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i , j ), C( i , j+1 ), C( i , j+2 ), C( i , j+3 ) C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) in the original matrix C In this version, we "inline" AddDot */ int p; /* First row */ // AddDot( k, &A( 0, 0 ), lda, &B( 0, 0 ), &C( 0, 0 ) ); for ( p=0; p<k; p++ ){ C( 0, 0 ) += A( 0, p ) * B( p, 0 ); } // AddDot( k, &A( 0, 0 ), lda, &B( 0, 1 ), &C( 0, 1 ) ); for ( p=0; p<k; p++ ){ C( 0, 1 ) += A( 0, p ) * B( p, 1 ); } // AddDot( k, &A( 0, 0 ), lda, &B( 0, 2 ), &C( 0, 2 ) ); for ( p=0; p<k; p++ ){ C( 0, 2 ) += A( 0, p ) * B( p, 2 ); } // AddDot( k, &A( 0, 0 ), lda, &B( 0, 3 ), &C( 0, 3 ) ); for ( p=0; p<k; p++ ){ C( 0, 3 ) += A( 0, p ) * B( p, 3 ); } /* Second row */ // AddDot( k, &A( 1, 0 ), lda, &B( 0, 0 ), &C( 1, 0 ) ); for ( p=0; p<k; p++ ){ C( 1, 0 ) += A( 1, p ) * B( p, 0 ); } // AddDot( k, &A( 1, 0 ), lda, &B( 0, 1 ), &C( 1, 1 ) ); for ( p=0; p<k; p++ ){ C( 1, 1 ) += A( 1, p ) * B( p, 1 ); } // AddDot( k, &A( 1, 0 ), lda, &B( 0, 2 ), &C( 1, 2 ) ); for ( p=0; p<k; p++ ){ C( 1, 2 ) += A( 1, p ) * B( p, 2 ); } // AddDot( k, &A( 1, 0 ), lda, &B( 0, 3 ), &C( 1, 3 ) ); for ( p=0; p<k; p++ ){ C( 1, 3 ) += A( 1, p ) * B( p, 3 ); } /* Third row */ // AddDot( k, &A( 2, 0 ), lda, &B( 0, 0 ), &C( 2, 0 ) ); for ( p=0; p<k; p++ ){ C( 2, 0 ) += A( 2, p ) * B( p, 0 ); } // AddDot( k, &A( 2, 0 ), lda, &B( 0, 1 ), &C( 2, 1 ) ); for ( p=0; p<k; p++ ){ C( 2, 1 ) += A( 2, p ) * B( p, 1 ); } // AddDot( k, &A( 2, 0 ), lda, &B( 0, 2 ), &C( 2, 2 ) ); for ( p=0; p<k; p++ ){ C( 2, 2 ) += A( 2, p ) * B( p, 2 ); } // AddDot( k, &A( 2, 0 ), lda, &B( 0, 3 ), &C( 2, 3 ) ); for ( p=0; p<k; p++ ){ C( 2, 3 ) += A( 2, p ) * B( p, 3 ); } /* Four row */ // AddDot( k, &A( 3, 0 ), lda, &B( 0, 0 ), &C( 3, 0 ) ); for ( p=0; p<k; p++ ){ C( 3, 0 ) += A( 3, p ) * B( p, 0 ); } // AddDot( k, &A( 3, 0 ), lda, &B( 0, 1 ), &C( 3, 1 ) ); for ( p=0; p<k; p++ ){ C( 3, 1 ) += A( 3, p ) * B( p, 1 ); } // AddDot( k, &A( 3, 0 ), lda, &B( 0, 2 ), &C( 3, 2 ) ); for ( p=0; p<k; p++ ){ C( 3, 2 ) += A( 3, p ) * B( p, 2 ); } // AddDot( k, &A( 3, 0 ), lda, &B( 0, 3 ), &C( 3, 3 ) ); for ( p=0; p<k; p++ ){ C( 3, 3 ) += A( 3, p ) * B( p, 3 ); } }
依然是A的unroll4,和之前1x4的思路一样。没有效果。估计下一步该整合到一个iter里了.
opt12
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot4x4( int, double *, int, double *, int, double *, int ); void AddDot( int, double *, int, double *, double * ); void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=4 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot4x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes a 4x4 block of matrix A C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ). C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ). C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i , j ), C( i , j+1 ), C( i , j+2 ), C( i , j+3 ) C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) in the original matrix C In this version, we merge each set of four loops, computing four inner products simultaneously. */ int p; for ( p=0; p<k; p++ ){ /* First row */ C( 0, 0 ) += A( 0, p ) * B( p, 0 ); C( 0, 1 ) += A( 0, p ) * B( p, 1 ); C( 0, 2 ) += A( 0, p ) * B( p, 2 ); C( 0, 3 ) += A( 0, p ) * B( p, 3 ); /* Second row */ C( 1, 0 ) += A( 1, p ) * B( p, 0 ); C( 1, 1 ) += A( 1, p ) * B( p, 1 ); C( 1, 2 ) += A( 1, p ) * B( p, 2 ); C( 1, 3 ) += A( 1, p ) * B( p, 3 ); /* Third row */ C( 2, 0 ) += A( 2, p ) * B( p, 0 ); C( 2, 1 ) += A( 2, p ) * B( p, 1 ); C( 2, 2 ) += A( 2, p ) * B( p, 2 ); C( 2, 3 ) += A( 2, p ) * B( p, 3 ); /* Fourth row */ C( 3, 0 ) += A( 3, p ) * B( p, 0 ); C( 3, 1 ) += A( 3, p ) * B( p, 1 ); C( 3, 2 ) += A( 3, p ) * B( p, 2 ); C( 3, 3 ) += A( 3, p ) * B( p, 3 ); } }
在1x4的优化中,分析了这是如何减少访存的,参考 opt5
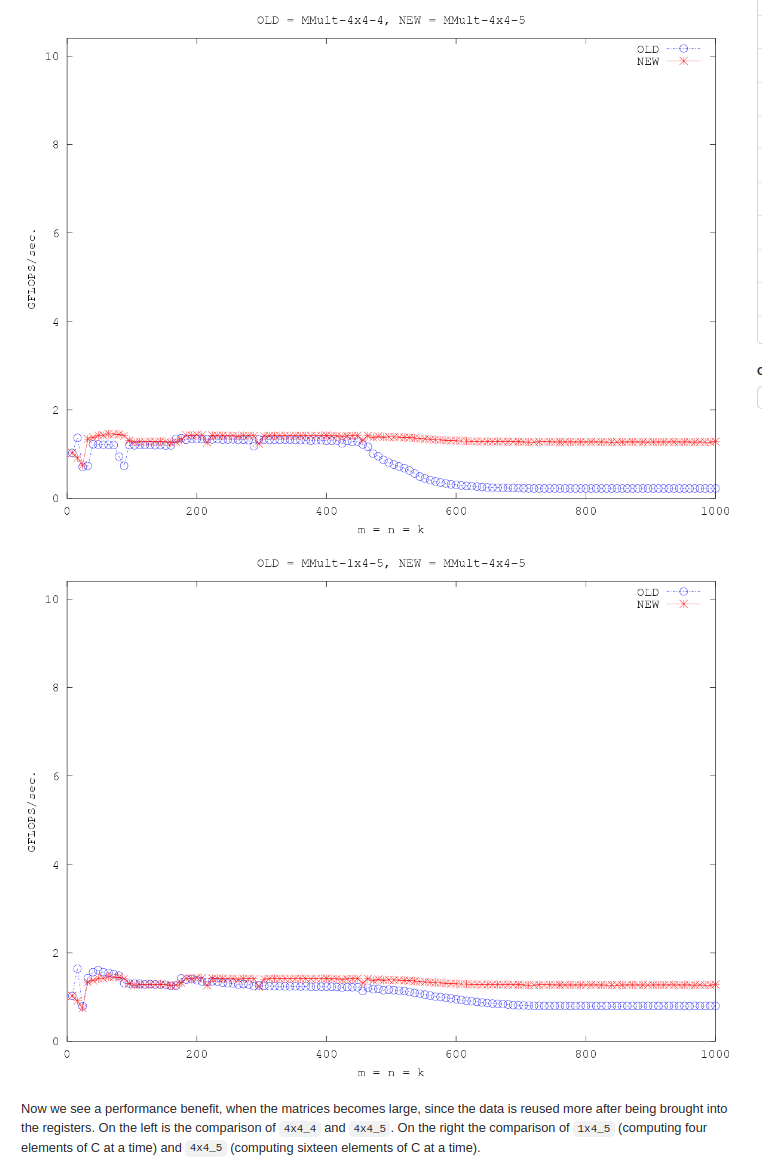
对比了这种访存模式下,1x4和4x4。4x4在problemsize较大时,效果也比较好。
opt13
Optimization_4x4_6
/* Create macros so that the matrices are stored in column-major order */ #define A(i,j) a[ (j)*lda + (i) ] #define B(i,j) b[ (j)*ldb + (i) ] #define C(i,j) c[ (j)*ldc + (i) ] /* Routine for computing C = A * B + C */ void AddDot4x4( int, double *, int, double *, int, double *, int ); void MY_MMult( int m, int n, int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { int i, j; for ( j=0; j<n; j+=4 ){ /* Loop over the columns of C, unrolled by 4 */ for ( i=0; i<m; i+=4 ){ /* Loop over the rows of C */ /* Update C( i,j ), C( i,j+1 ), C( i,j+2 ), and C( i,j+3 ) in one routine (four inner products) */ AddDot4x4( k, &A( i,0 ), lda, &B( 0,j ), ldb, &C( i,j ), ldc ); } } } void AddDot4x4( int k, double *a, int lda, double *b, int ldb, double *c, int ldc ) { /* So, this routine computes a 4x4 block of matrix A C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ). C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ). C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ). C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ). Notice that this routine is called with c = C( i, j ) in the previous routine, so these are actually the elements C( i , j ), C( i , j+1 ), C( i , j+2 ), C( i , j+3 ) C( i+1, j ), C( i+1, j+1 ), C( i+1, j+2 ), C( i+1, j+3 ) C( i+2, j ), C( i+2, j+1 ), C( i+2, j+2 ), C( i+2, j+3 ) C( i+3, j ), C( i+3, j+1 ), C( i+3, j+2 ), C( i+3, j+3 ) in the original matrix C In this version, we accumulate in registers and put A( 0, p ) in a register */ int p; register double /* hold contributions to C( 0, 0 ), C( 0, 1 ), C( 0, 2 ), C( 0, 3 ) C( 1, 0 ), C( 1, 1 ), C( 1, 2 ), C( 1, 3 ) C( 2, 0 ), C( 2, 1 ), C( 2, 2 ), C( 2, 3 ) C( 3, 0 ), C( 3, 1 ), C( 3, 2 ), C( 3, 3 ) */ c_00_reg, c_01_reg, c_02_reg, c_03_reg, c_10_reg, c_11_reg, c_12_reg, c_13_reg, c_20_reg, c_21_reg, c_22_reg, c_23_reg, c_30_reg, c_31_reg, c_32_reg, c_33_reg, /* hold A( 0, p ) A( 1, p ) A( 2, p ) A( 3, p ) */ a_0p_reg, a_1p_reg, a_2p_reg, a_3p_reg; c_00_reg = 0.0; c_01_reg = 0.0; c_02_reg = 0.0; c_03_reg = 0.0; c_10_reg = 0.0; c_11_reg = 0.0; c_12_reg = 0.0; c_13_reg = 0.0; c_20_reg = 0.0; c_21_reg = 0.0; c_22_reg = 0.0; c_23_reg = 0.0; c_30_reg = 0.0; c_31_reg = 0.0; c_32_reg = 0.0; c_33_reg = 0.0; for ( p=0; p<k; p++ ){ a_0p_reg = A( 0, p ); a_1p_reg = A( 1, p ); a_2p_reg = A( 2, p ); a_3p_reg = A( 3, p ); /* First row */ c_00_reg += a_0p_reg * B( p, 0 ); c_01_reg += a_0p_reg * B( p, 1 ); c_02_reg += a_0p_reg * B( p, 2 ); c_03_reg += a_0p_reg * B( p, 3 ); /* Second row */ c_10_reg += a_1p_reg * B( p, 0 ); c_11_reg += a_1p_reg * B( p, 1 ); c_12_reg += a_1p_reg * B( p, 2 ); c_13_reg += a_1p_reg * B( p, 3 ); /* Third row */ c_20_reg += a_2p_reg * B( p, 0 ); c_21_reg += a_2p_reg * B( p, 1 ); c_22_reg += a_2p_reg * B( p, 2 ); c_23_reg += a_2p_reg * B( p, 3 ); /* Four row */ c_30_reg += a_3p_reg * B( p, 0 ); c_31_reg += a_3p_reg * B( p, 1 ); c_32_reg += a_3p_reg * B( p, 2 ); c_33_reg += a_3p_reg * B( p, 3 ); } C( 0, 0 ) += c_00_reg; C( 0, 1 ) += c_01_reg; C( 0, 2 ) += c_02_reg; C( 0, 3 ) += c_03_reg; C( 1, 0 ) += c_10_reg; C( 1, 1 ) += c_11_reg; C( 1, 2 ) += c_12_reg; C( 1, 3 ) += c_13_reg; C( 2, 0 ) += c_20_reg; C( 2, 1 ) += c_21_reg; C( 2, 2 ) += c_22_reg; C( 2, 3 ) += c_23_reg; C( 3, 0 ) += c_30_reg; C( 3, 1 ) += c_31_reg; C( 3, 2 ) += c_32_reg; C( 3, 3 ) += c_33_reg; }
与1x4相同,把A和C放入寄存器,减少访存。
本文来自博客园,作者:ijpq,转载请注明原文链接:https://www.cnblogs.com/ijpq/p/18110344





【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· 被坑几百块钱后,我竟然真的恢复了删除的微信聊天记录!
· 没有Manus邀请码?试试免邀请码的MGX或者开源的OpenManus吧
· 【自荐】一款简洁、开源的在线白板工具 Drawnix
· 园子的第一款AI主题卫衣上架——"HELLO! HOW CAN I ASSIST YOU TODAY
· Docker 太简单,K8s 太复杂?w7panel 让容器管理更轻松!