CUTLASS: Fast Linear Algebra in CUDA C++

https://developer.nvidia.com/blog/cutlass-linear-algebra-cuda/

Efficient Matrix Multiplication on GPUs

计算密集度 = (时间复杂度/空间复杂度) = O(N^3)/O(N^2) = O(N)

// naive
for (int i = 0; i < M; ++i)
    for (int j = 0; j < N; ++j)
       for (int k = 0; k < K; ++k) 
            C[i][j] += A[i][k] * B[k][j];

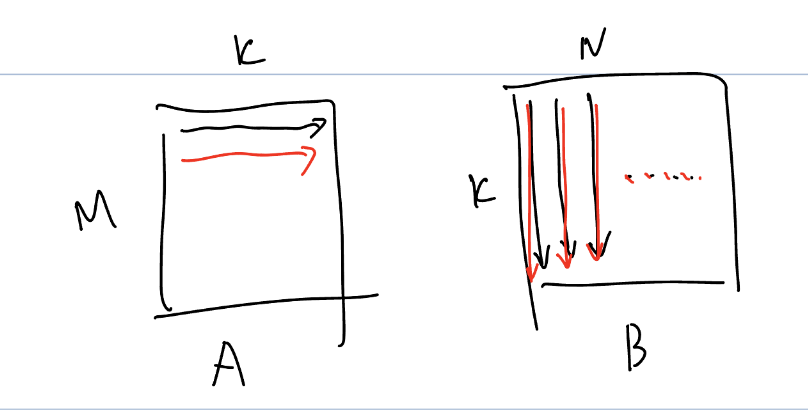
对于A的每一行，都会读取一整个B矩阵. 能否达到O(N)的复用次数？B中的元素按照列来访问，那么每次重新读取B[0,0]时是重新进行访存的。而实际上，读取一次B[0,0]只进行了1次计算。

---

// opt 1
for (int k = 0; k < K; ++k)     // K dimension now outer-most loop
    for (int i = 0; i < M; ++i)
        for (int j = 0; j < N; ++j)
            C[i][j] += A[i][k] * B[k][j];

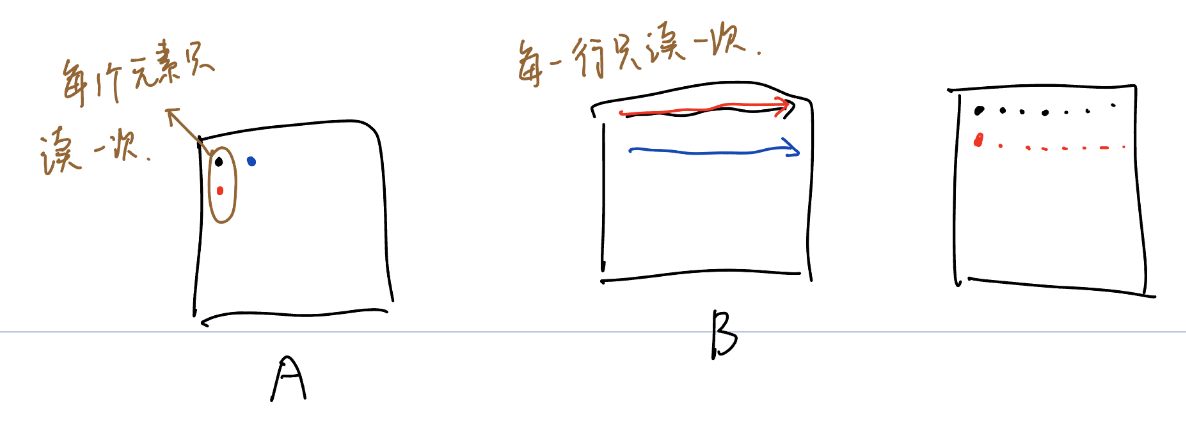
对于A[0,0]，只读取一次，但执行j=0~N-1，共N次计算。
对于B[0,0]，读取i=0~M-1，j=0, 共M次，执行这M次计算，并且这里可能会cache住，所以实际读取次数可能小于M。
对于C[0,0]，读取k=0~K-1,共K次。执行K次(k=0~K-1, i=0,j=0)计算。
理论上已经比naive更接近于计算密集度O(N)

但这个计算依赖于每一次写入C中的元素时，这个元素的读取，写入速度能和乘法指令一样快，也就是说这些C中的元素最好能一直在cache中，而不发生trash。否则，这个计算过程就会使依赖于访存。

// opt 2
for (int m = 0; m < M; m += Mtile)                // iterate over M dimension
    for (int n = 0; n < N; n += Ntile)            // iterate over N dimension
        for (int k = 0; k < K; ++k)
            for (int i = 0; i < Mtile; ++i)       // compute one tile 
                for (int j = 0; j < Ntile; ++j) {
                    int row = m + i;
                    int col = n + j;
                    C[row][col] += A[row][k] * B[k][col];
                }

这样，在tile够小的时候，tile中元素就能放到cache中。