位运算操作

bit operations

• /2, *2

  

• odd or even

• 实现mod

  当计算\(a \mod b\) 且 b是\(2^n\)时，可以直接使用\(a \& (b-1)\)来计算\(a \mod b\)​。

  原理为：$a \mod b \(是\)a/b$​的余数。

  因为\(b=2^n\),\(a/2^n\)又可以转换为a=a>>n;

  所以$ a \mod b $​​ = a - (a//b)*b = \(a - (a//2^n)*2^n\)​

  所以\(a \mod b\) = a - (a>>n)<<n

  又因为right shift是截断的，所以(a>>n)<<n的结果是将a的低n位置0,记为\(a'\)

  所以\(a - a' = a + (-a') = a + ( \sim a'+1)\)​

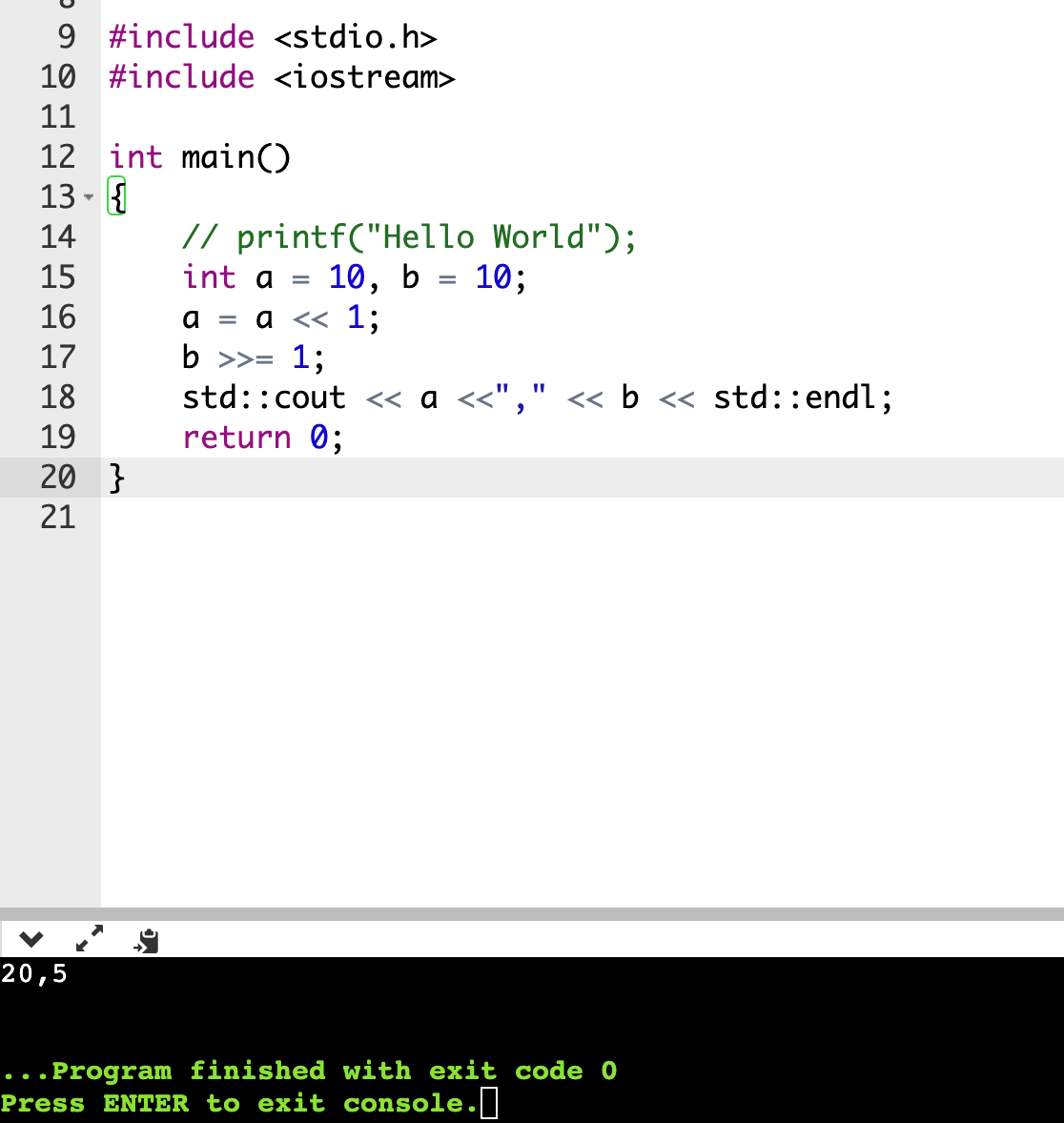
  • 关于\(a - a'\) = 低n位的推导

    

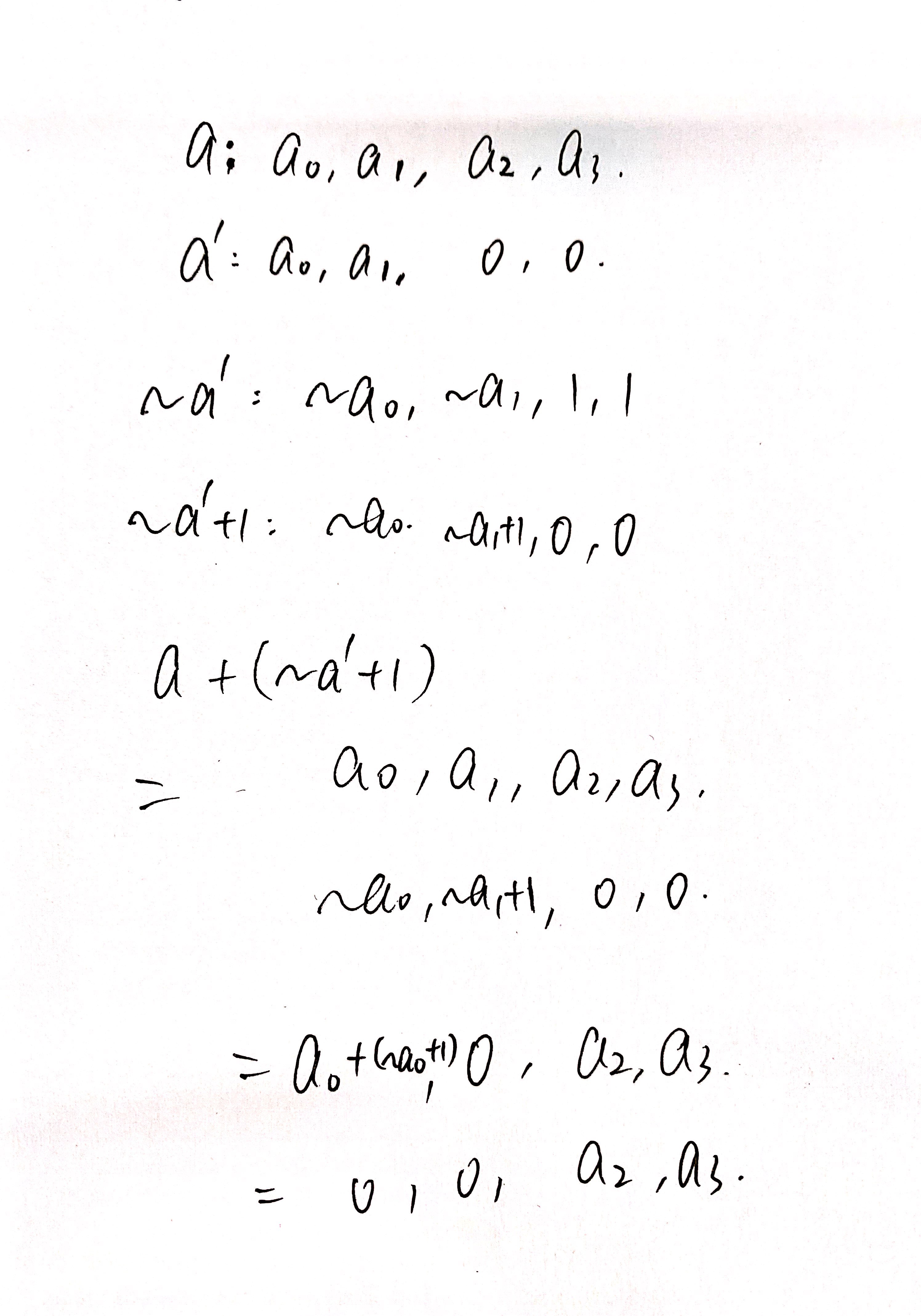
综上，可以得到结论：这个低n位就是mod运算的结果（余数）

所以，\(b-1=2^n-1\)，二进制表示为n-1位全1

所以，\(a\&(b-1)\)就是取a的低n位，就是余数,即mod运算结果

• 求商

  经过上面的推导，发现计算\(a \mod b\)当\(b=2^n\)时，a的低n位是余数，高m-n位是商。高m-n位是商的原因是：商应为\(a//b = a//2^n\) = a右移n位后的值，当a是正数时，符号位扩展一直是0，所以商是a的高m-n位。所以在这种情况下，求商的方法就是取a的高m-n位，之前取a的低n位操作是a&(b-1)，那么现在就是a&~(b-1)。这个操作可以在ispc的tutorial中看到：https://ispc.github.io/perfguide.html

  • counting leading zero (CLZ)

template <typename value_t>
CUTLASS_HOST_DEVICE value_t clz(value_t x) {
    for (int i = 31; i >= 0; --i) {
        if ((1 << i) & x)
            return 31 - i;
    }
    return 32;
}

• find_log2(找到>=x的2^n)

template <typename value_t>
CUTLASS_HOST_DEVICE value_t find_log2(value_t x) {
    int a = int(31 - clz(x));
    a += (x & (x - 1)) != 0;  // Round up, add 1 if not a power of 2.
    return a;
}

• find_divisor

void find_divisor(unsigned int& mul, unsigned int& shr, unsigned int denom) {
    if (denom == 1) {
        mul = 0;
        shr = 0;
    } else {
        unsigned int p = 31 + find_log2(denom);
        unsigned m =
                unsigned(((1ull << p) + unsigned(denom) - 1) / unsigned(denom));

        mul = m;
        shr = p - 32;
    }
}

解释：
在计算a/b时，由于除法的速度比较慢，所以可以采用这种方法优化
a/b=a(1/b)
x=(1<<16)/b
a/b=(a*x)>>16
在逻辑上，a/b等价于a(1/b)，但希望避免除法，所以这里使用(1<<16)/b。
为什么呢？因为，1<<16是一个固定点数，1000 0000 0000 0000 0，这里假设第16位（即1）之后表示的是小数。之后，计算(1<<16)/b时，仍然假设16位之后是小数部分。这时，得到了一个x

如果按照原计算，每次计算a/b都是一次除法
而按照现方案，可以把1<<16/b保存起来，假设b是固定的n个数，那么这里就产生n个除法。但是之后再计算a/b时，都使用a*x一次乘法，和>>16这个右移操作，就完全不再使用除法了。

这里还有一个问题，这个位移数如何选择？

例如，
a=11, b = 5
a/b = 2, 这里存在浮点数运算
而1<<16/b = 65536/5=13107
a*x=11 x 13107 = 144177
再>>16，得到2