【SAM】BZOJ3998-弦论
【题目大意】
给出一个字符串,求第k大的子串。(输入1表示子串可重复,0表示不可重复)
【思路】
显然,k大子串是后缀自动机的经典题型,可以利用后缀自动机的性质来解决。对于字符串
[前铺1]"abcbc",我们可以画出它的后缀自动机,如下图:
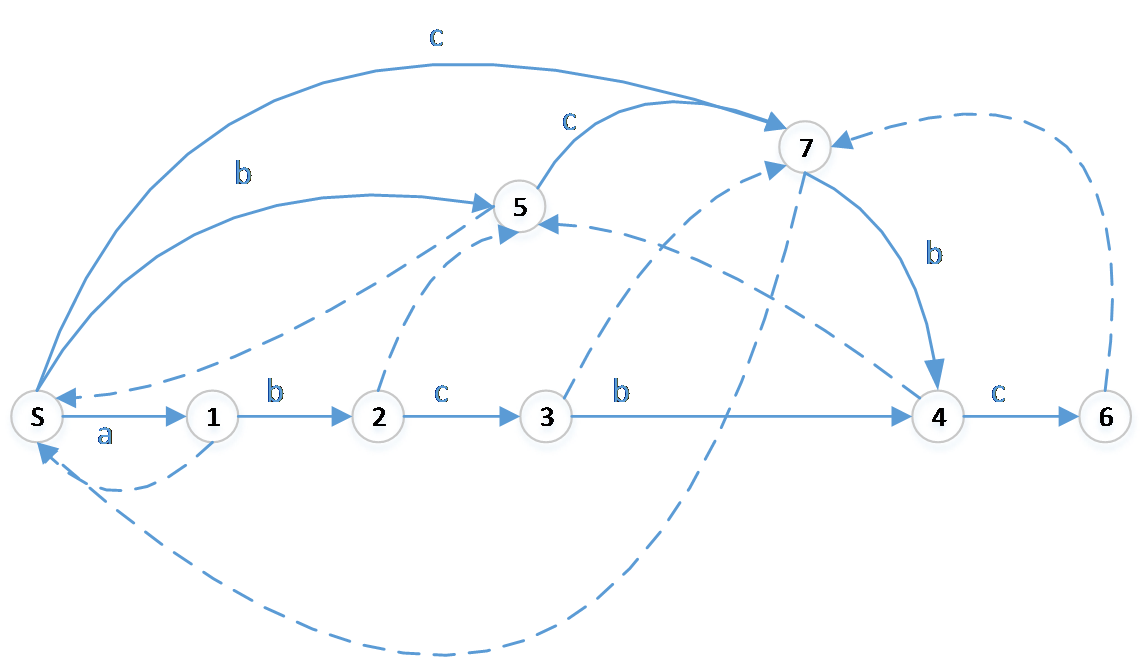
Pre树类似于AC自动机中的fail树,即将pre方向形成一棵树。对于上图,它的pre树如下:

[前铺2]考虑字符串s的任意非空子串t。我们称终点集合right(t)为:s中所有是t出现位置终点的集合。例如:对于字符串ATCGTCGT来说,所有的CG的末尾位置的集合是{4,7},也就是说right(“CG”)={4,7}。如果两个子串t_1和t_2终点集合一致,即right(t_1)=right(t_2),那么称它们为“终点等价”。因此,所有s的非空子串可以根据终点等价性分成若干类。
例如:对于字符串abcbc来说,它的所有子串构成的集合可以按照上述等价关系进行如下划分:{{a},{b},{c,bc},{ab},{cb,bcb,abcb},{abc},{cbc,bcbc,abcbc}}。
【知识点】pre树和right集合之间的关系
①除S以外的每个节点代表一个终点等价类。
②每个节点对应的等价类的right集合大小等于以它为根的子树的叶子节点的数量。
right等价类:
right{a}={1}
right{b}={2,4}
right{c,bc}={3,5}
right{ab} ={2}
right{cb,bcb,abcb} ={4}
right{abc} ={3}
right{cbc,bcbc,abcbc}={5}
我们用s[i]表示i所在的等价类的right集合大小,等于在pre树上以它为根的子树的叶子节点的数量。当sign=1时,s[i]=∑s[j](j为i在pre树上的孩子);当sign=0时,s[i]=1。对于sign=1的情况,显然孩子节点的step值大于父亲,所以我们只需要按照step值进行拓扑排序,从后往前进行累加即可得到s[i]的值。
对于叶子节点(叶子节点一定是非后添加的节点,即原字符串中产生的,图中的水平一行),初值在extend中产生:
1 s[np]=1;
假设q[i]为拓扑排序后的序列,则如下累加即可:
1 for(int i=tot;i>=1;i--) 2 { 3 if(sign==1) s[pre[q[i]]]+=s[q[i]]; 4 else s[q[i]]=1; 5 } 6 s[1]=0;//不要忘了根节点是虚点
【解题过程】
①根据上述知识点中的性质,如何进行拓扑排序呢?
1 for(int i=1;i<=tot;i++) 2 v[step[i]]++;//累加每个step[i]的个数 3 for(int i=1;i<=tot;i++) 4 v[i]+=v[i-1];//v[i]表示按step值从小到大的顺序排序后,step值为i的数在q数组中最右端的下标 5 for(int i=tot;i>=1;i--) 6 q[v[step[i]]--]=i;//每次将当前的i放入对应step[i]最右端的位置,然后将step[i]的最右端左移
简单地说可以理解为:将当前序列按照step值从小到大排序,对于相同的step值按照原来的出现顺序(下标顺序)从后到前排序。
如以下情况(实际的后缀自动机中是不会出现下面的例子的,这里仅仅方便理解用)
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
Step[i] |
1 |
2 |
3 |
2 |
4 |
2 |
3 |
求step[i]的前最后和可得到:
|
i |
1 |
2 |
3 |
4 |
|
V[i] |
1 |
4 |
6 |
7 |
所以相当于得到了这样一张表格:
|
step值 |
1 |
2 |
2 |
2 |
3 |
3 |
4 |
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
q[i] |
★ |
|
|
★ |
|
★ |
★ |
★处即对应上面v[i]的值,表示按step值从小到大的顺序排序后,step值为i的数在q数组中最右端的下标。从后往前依次按照step值填入★处,然后对应的v[step[i]]减一,即将★左移一位。最后我们可以得到这样的结果:
|
step值 |
1 |
2 |
2 |
2 |
3 |
3 |
4 |
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
q[i] |
1 |
2 |
4 |
6 |
3 |
7 |
5 |
②Sum值代表从当前状态出发不同的路径条数,即将孩子们的路径条数累加起来,再加上本身的s值。即sum[i]=s[i]+∑sum[j](j=next[i][k],k=0..25)
1 for(int i=tot;i>=1;i--) 2 { 3 sum[q[i]]+=s[q[i]]; 4 for(int j=0;j<26;j++) sum[q[i]]+=sum[next[q[i]][j]]; 5 }
③预处理结束之后,通过dfs找出第k小的路径。这有点类似与二十六分,每次先按字典序往后走,如果当前节点的s值大于当前的k,则说明到当前节点为止,退出dfs;否则k先减去当前s的大小。如果当前节点的sum值大于当前的k值,说明终止点再它的孩子中,输出当前节点对应的字母,k并继续往下深dfs;如果当前结点的sum值小于k,说明k大的子串不在这条路径上,直接将k减去sum并继续搜索下一条路径。(说起来有点绕,直接看代码)
1 if (k<=s[d]) return; 2 k-=s[d]; 3 for (int i=0;i<26;i++) 4 { 5 int tmp=next[d][i]; 6 if (tmp>0) 7 { 8 if (k<=sum[tmp]) 9 { 10 printf("%c",i+'a'); 11 dfs(tmp,k); 12 return; 13 } 14 k-=sum[tmp]; 15 } 16 }
----搞了好久啊这道题,网上的大家都说是水题,可以得:D那我这个蒟蒻就以非常狼狈的姿势“水”过去好啦。以下代(正)码(文):
1 #include<iostream> 2 #include<cstdio> 3 #include<cstring> 4 #include<algorithm> 5 using namespace std; 6 const int MAXN=500000+50; 7 char str[MAXN]; 8 int len,sign,k; 9 10 struct SAM 11 { 12 int step[MAXN*2],pre[MAXN*2],next[MAXN*2][26],q[MAXN*2]; 13 int v[MAXN*2],s[MAXN*2],sum[MAXN*2]; 14 int tot,last; 15 inline int newNode(int cnt) 16 { 17 step[++tot]=cnt; 18 pre[tot]=0; 19 for (int i=0;i<26;i++) next[tot][i]=0; 20 return tot; 21 } 22 23 inline void extend(int x) 24 { 25 int p=last; 26 int np=newNode(step[last]+1); 27 s[np]=1; 28 while (p && !next[p][x]) next[p][x]=np,p=pre[p]; 29 if (!p) pre[np]=1; 30 else 31 { 32 int q=next[p][x]; 33 if (step[q]==step[p]+1) pre[np]=q; 34 else 35 { 36 int nq=newNode(step[p]+1); 37 for (int i=0;i<26;i++) next[nq][i]=next[q][i]; 38 pre[nq]=pre[q]; 39 pre[q]=pre[np]=nq; 40 while (p && next[p][x]==q) next[p][x]=nq,p=pre[p]; 41 } 42 } 43 last=np; 44 } 45 inline void clear() 46 { 47 tot=0; 48 last=newNode(0); 49 } 50 51 inline void prep() 52 { 53 for(int i=1;i<=tot;i++) 54 v[step[i]]++;//累加每个step[i]的个数 55 for(int i=1;i<=tot;i++) 56 v[i]+=v[i-1];//v[i]表示按step值从小到大的顺序排序后,step值为i的数在q数组中最右端的下标 57 for(int i=tot;i>=1;i--) 58 q[v[step[i]]--]=i;//每次将当前的i放入对应step[i]最右端的位置,然后将step[i]的最右端左移 59 for(int i=tot;i>=1;i--) 60 { 61 if(sign==1) s[pre[q[i]]]+=s[q[i]]; 62 else s[q[i]]=1; 63 } 64 s[1]=0;//不要忘了根节点是虚点 65 for(int i=tot;i>=1;i--) 66 { 67 sum[q[i]]+=s[q[i]]; 68 for(int j=0;j<26;j++) sum[q[i]]+=sum[next[q[i]][j]]; 69 } 70 } 71 72 inline void dfs(int d,int k) 73 { 74 if (k<=s[d]) return; 75 k-=s[d]; 76 for (int i=0;i<26;i++) 77 { 78 int tmp=next[d][i]; 79 if (tmp>0) 80 { 81 if (k<=sum[tmp]) 82 { 83 printf("%c",i+'a'); 84 dfs(tmp,k); 85 return; 86 } 87 k-=sum[tmp]; 88 } 89 } 90 } 91 }suf; 92 93 void init() 94 { 95 scanf("%s",str); 96 suf.clear(); 97 len=strlen(str); 98 for (int i=0;i<len;i++) suf.extend(str[i]-'a'); 99 scanf("%d%d",&sign,&k); 100 } 101 102 int main() 103 { 104 init(); 105 suf.prep(); 106 suf.dfs(1,k); 107 return 0; 108 }


 浙公网安备 33010602011771号
浙公网安备 33010602011771号