【平面图最小割】BZOJ1001- [BeiJing2006]狼抓兔子

【题目大意】
左上角点为(1,1),右下角点为(N,M)(上图中N=4,M=5).有以下三种类型的道路
1:(x,y)<==>(x+1,y)
2:(x,y)<==>(x,y+1)
3:(x,y)<==>(x+1,y+1)
道路上的权值表示这条路上最多能够通过的兔子数，道路是无向的。开始时所有的兔子都聚集在左上角(1,1)的窝里，现在它们要跑到右下解(N,M)的窝中去，如果一条道路上最多通过的兔子数为K，需要同样数量的K只狼伏击，求封锁道路的最小狼数。

【思路】
显然这是最小割，但是最小割效率太低。可以发现这是一张平面图，根据平面图的性质，平面图最小割=对偶图的最短路。所谓对偶图，简单理解就是把面转为点，然后将面之间的边作为连接两个点的边。本题中建立的对偶图如下：

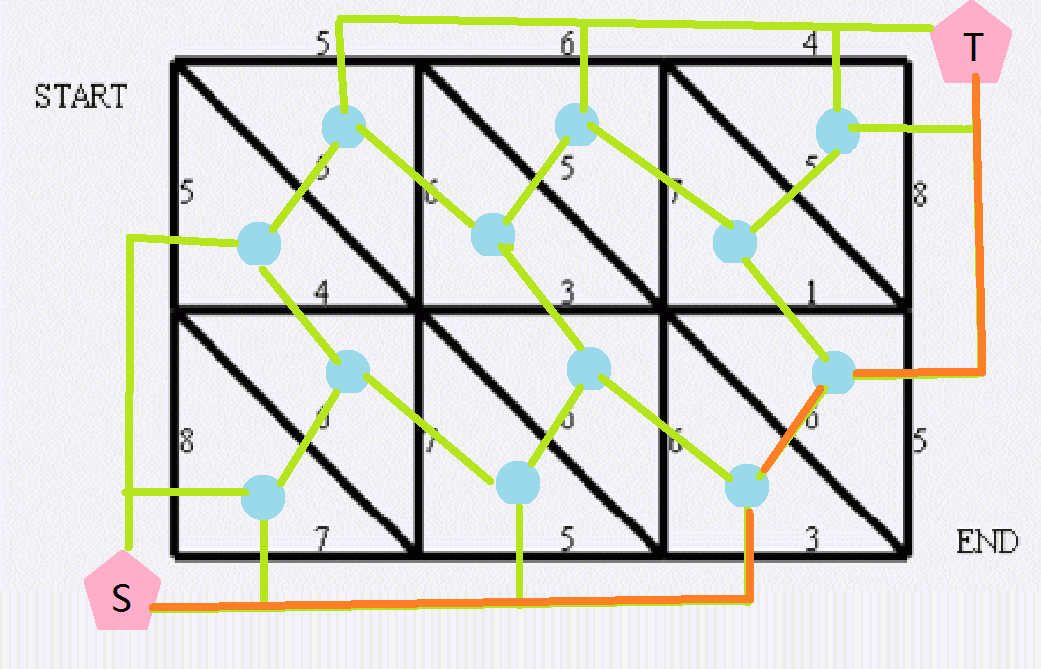
显然可以发现，最短路必然是最小割。

【错误点】
注意一下面转点后，对偶图点的数量和原来点的数量不一样，大概为2倍，数组要开足够大，否则RE！

 1 #include<iostream>
 2 #include<cstdio>
 3 #include<cstring>
 4 #include<algorithm>
 5 #include<vector>
 6 #include<queue>
 7 #include <utility>
 8 #define S 0
 9 #define T 2*(m-1)*(n-1)+1
10 using namespace std;
11 const int MAXN=2000000;
12 const int INF=0x7fffffff;
13 struct edge
14 {
15     int fr,to,len;
16 };
17 int n,m,w;
18 vector<edge> E[MAXN];
19   
20 void addedge(int u,int v,int w)
21 {
22     //cout<<"!"<<u<<' '<<v<<' '<<w<<endl;
23     E[u].push_back((edge){u,v,w});
24     E[v].push_back((edge){v,u,w});
25 }
26   
27 int dijkstra()
28 {
29     priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > > que;
30     int dis[MAXN],vis[MAXN];
31     memset(vis,0,sizeof(vis));
32     for (int i=S+1;i<=T;i++) dis[i]=INF;
33     dis[S]=0;
34     que.push(make_pair<int,int>(0,S));
35     while (!que.empty())
36     {
37         int head=que.top().second;que.pop();
38         if (!vis[head])
39         {
40             vis[head]=1;
41             for (int i=0;i<E[head].size();i++)
42             {
43                 edge Edge=E[head][i];
44                 if (!vis[Edge.to] && dis[Edge.to]>dis[Edge.fr]+Edge.len)
45                 {
46                     dis[Edge.to]=dis[Edge.fr]+Edge.len;
47                     que.push(make_pair<int,int>(dis[Edge.to],Edge.to));
48                 }
49             }
50         }
51     }
52     return (dis[T]);
53 }
54   
55 void init()
56 {
57     for (int i=0;i<n;i++)    
58         for (int j=0;j<m-1;j++)
59         {
60             scanf("%d",&w);
61             if (i==0) addedge(2*(j+1),T,w);
62                 else if (i==n-1) addedge(S,(n-2)*(m-1)*2+2*j+1,w);
63                     else addedge((i-1)*(m-1)*2+2*j+1,i*(m-1)*2+2*j+2,w);
64         }
65     for (int i=0;i<n-1;i++)
66         for (int j=0;j<m;j++)
67         {
68             scanf("%d",&w);
69             if (j==0) addedge(S,i*2*(m-1)+1,w);
70                 else if (j==m-1) addedge((i+1)*2*(m-1),T,w);
71                     else addedge(i*2*(m-1)+j*2,i*2*(m-1)+2*j+1,w);
72         }
73     for (int i=0;i<(n-1);i++)
74         for (int j=0;j<(m-1);j++) 
75         {
76             scanf("%d",&w);
77             //cout<<i<<' '<<j<<' ';
78             addedge(i*2*(m-1)+2*j+1,i*2*(m-1)+2*j+2,w);
79         }
80 }
81   
82 int main()
83 {
84     scanf("%d%d",&n,&m);
85     if (n==1 && m==1) cout<<0<<endl;
86         else
87         {
88             init();
89             cout<<dijkstra()<<endl;
90         }
91     return 0;
92 }

 

posted @ 2016-07-17 23:09  iiyiyi  阅读(301)  评论(0)  编辑  收藏  举报