立体几何之三视图-逆投影-简单篇

############################

首先，我给出一个标准：

什么叫真正会三视图还原为直观？

    那就是网上任意给你一道三视图还原为直观图的题目，你都能在6分钟左右得出正确的答案，那么你就真正掌握了。

 

 

我的遭遇：

1）首先，在我高中阶段，我从来就没有真正搞懂三视图，当时也只是乞求高考千万别考这玩意，也是最怕三视图还原直观图，只能应付简单的三视图还原。

2）真是应了那句“怕什么来什么”，以为高中过去了，不会的就让他过去吧。然而，到了大学，又遇到了机械制图，结果还挂科了，让我忌惮有恼火，同样也打击了我写一本高中数学书的小梦想。

3）直到在2017年左右，本人正式下定决心要写一本高中数学辅导书后。就必须彻底把这个玩意给搞定，于是在学校图书馆到处搜索三视图内容，前几天毫无收获，搜到的都是些笼统的实用性差的方法，随便找几个例子都不能解决问题。

4）大约三个月后再次四处搜索，终于不负有心人，找到了一篇高水准的论文，至此，才从根本上解决问题。

 

三视图现状：

1）能够学到该方法的学生太少了，只掌握在极少数同学手中。

2）部分高中数学老师可能主要靠经验，然而问题是学生是没有那么多时间去积累的，必须给学生提供最优秀的方法才能让他们学得好。

3）有的学生对三视图有恐惧心里，误以为需要很好的空间想象力。

4）有的学生大量刷题，结果还是会时不时遇到自己搞不定的三视图题目，进而遭遇打击，甚至认为自己想象力差。

5）我的检验标准是：任意在网上给你一道三视图题目，你在6分钟内得到正确答案。如果你能做到，那么你就真正掌握了三视图还原为直观图的最佳方法。

 

大量题目验证：

1）验证了5868道三视图题目。

2）总共花了我三天四夜的时间，至少要让我能见到的题目都得过关，不然我不敢贸然给大家分享。

3）用该方法还给组卷网纠错了十几道三视图的题目，当然了，组卷网很快就下架了相应的题目。

4）截图了其中500道不错的题目，再经过层层筛选去重，选择其中最具代表的题目，作为我的例题再分享给大家

 

该方法优势：

1）高效。

2）通用。

3）简洁。

4）可操作性强。

因此，大家再遇到三视图题目，学到了这个方法后，你决不应该丢分。

这也不需要你什么空间想象力，按部就班即可，这也是目前为止，解决三视图还原直观的最优秀方法了。

 

 

工地搬砖必备技术

 

 

 

例题一：

 

如下图，网格上的小正方形边长为1，粗实线是某几何体的三视图，该几何体的体积为   2       

 

 

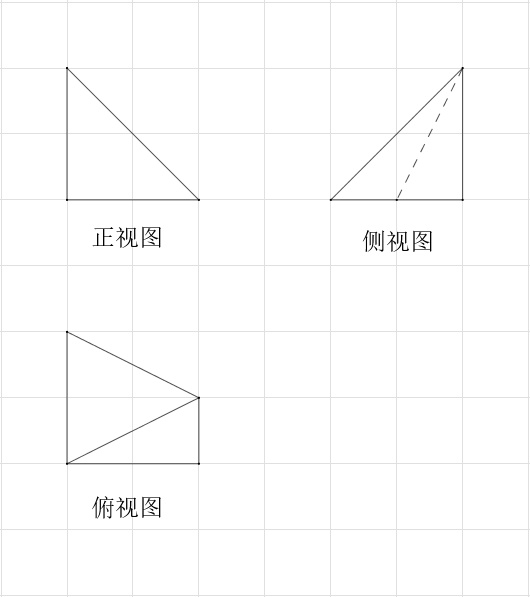
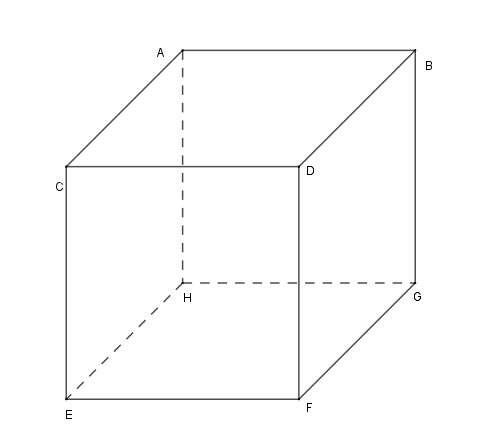
 第一步：根据三视图得到长方体，其长宽高均为2，如下图：

如何获得？

1）长方体的长由正视图的水平最大长度和俯视图的水平最大长度均可确定。

2）长方体的宽由侧视图的水平最大长度和俯视图竖直最大长度均可确定。

3）长方体的高由正视图竖直最大长度或者侧视图的竖直最大长度均可确定。

 

 

 

 

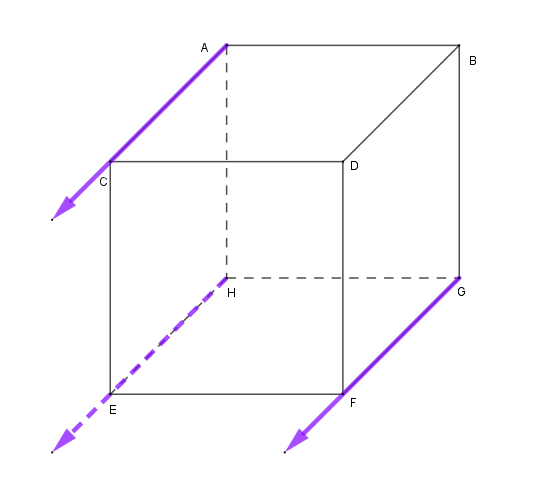
 第二步：根据正视图作逆投影线，如下图：

 

 

 

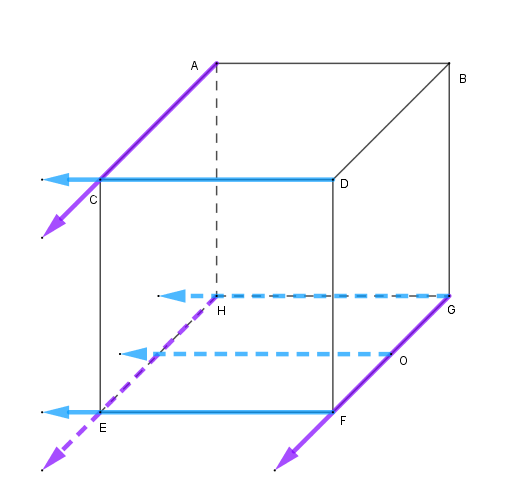
 第三步：根据侧视图作逆投影线，如下图：

 

 

 

 第四步：根据俯视图作逆投影线，如下图：

 

 

 

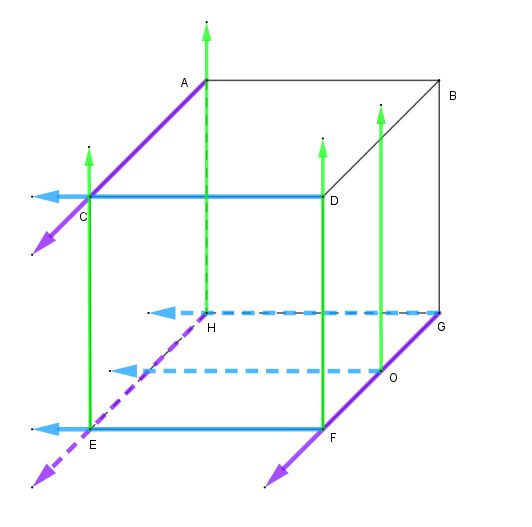
 第五步：获得可疑点，如下图：

 

 

 

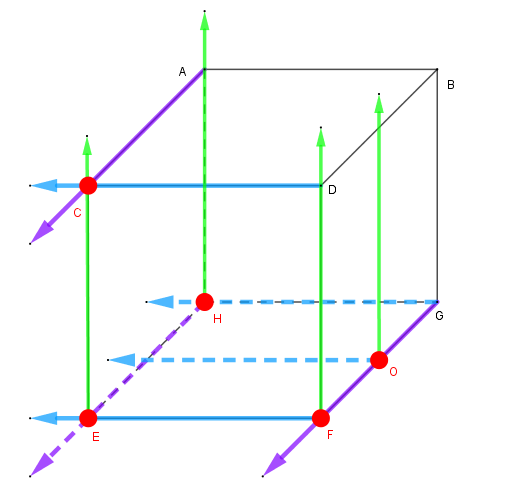
 第六步：根据三视图确认最优点，然后去掉逆投影线，并按照三视图而连接最优点：

 

 

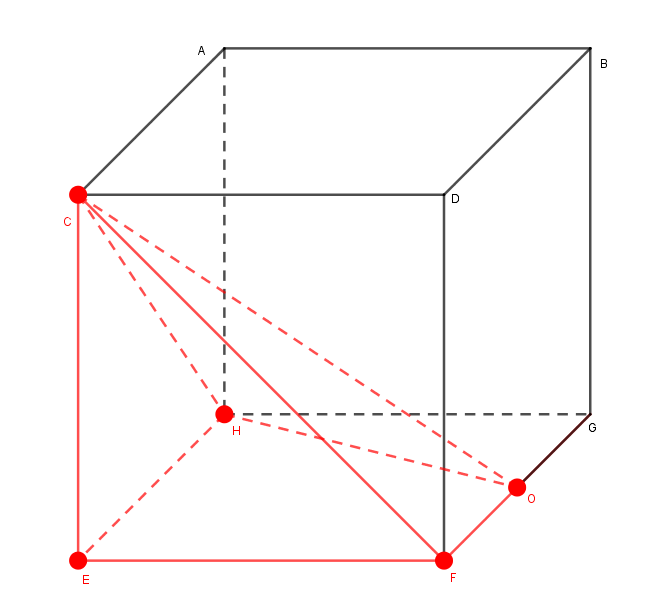
例题：

 

 

 

 

 

 

 

 

 

 

 

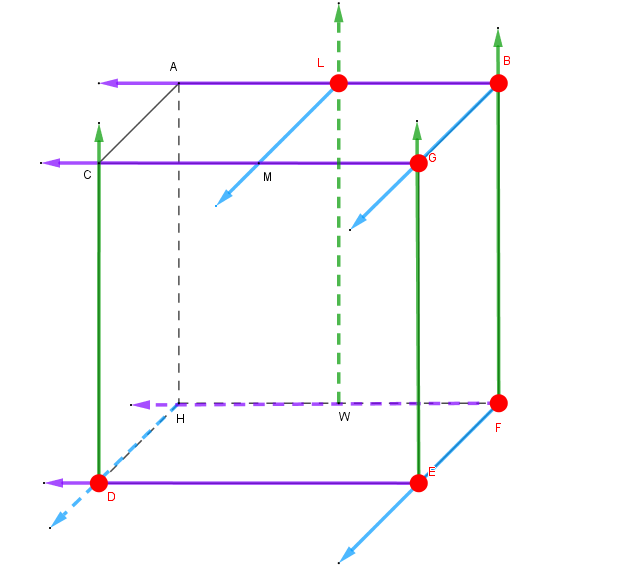
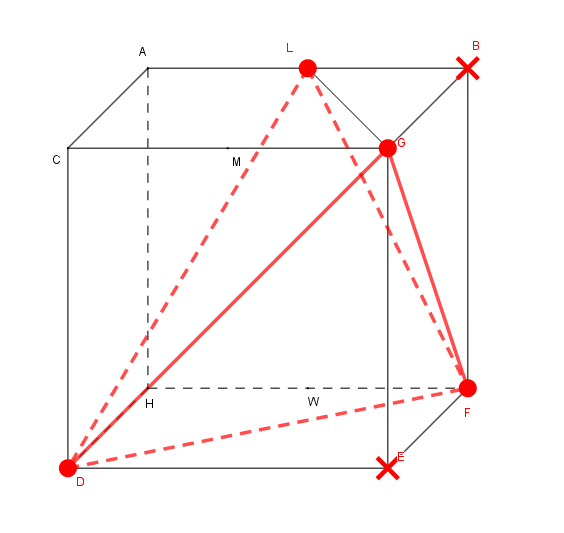
 例题：

 

 

 

 

 

 

 

 

高效通用：

 

 

 

 

 

 

 

 

 

 

 

 

三视图属于较难的题目

 

#################################