015-平衡二叉树(一)
1)、LL:LeftLeft,也称为"左左"。插入或删除一个节点后,根节点的左子树的左子树还有非空子节点,导致"根的左子树的高度"比"根的右子树的高度"大2,导致AVL树失去了平衡。
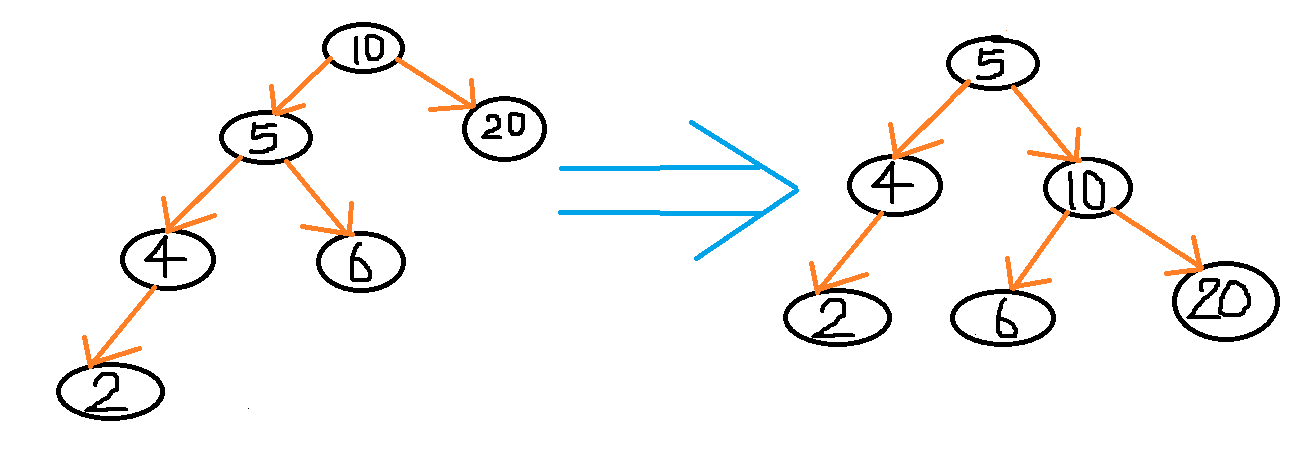
例如,在下面LL情况中,由于"根节点(10)的左子树(5)的左子树(4)还有非空子节点",而"根节点(10)的右子树(20)没有子节点";导致"根节点(10)的左子树(5)高度"比"根节点(10)的右子树(20)"高2。
解决办法如下图的旋转:
对于(10)号的左子树(5)也可能没有右子树(6)。那么从左图到右图的具体过程有哪些?
对于(5)号有:父亲节点需要改变;右子树需要改变。
对于(10)号有:父亲节点需要改变;左子树需要改变。
对于(6)号有:父亲节点需要改变。
另外高度需要调整。
具体过程是:第一,先保存(5)号节点;第二,截断(5)号的右子树(6)给(10)号的左子树;第三,将(10)号作为(5)号的右子树。
左左情况:一是:左左左,二是左左右。这两种情况可以合并处理,和上面处理完全一样。

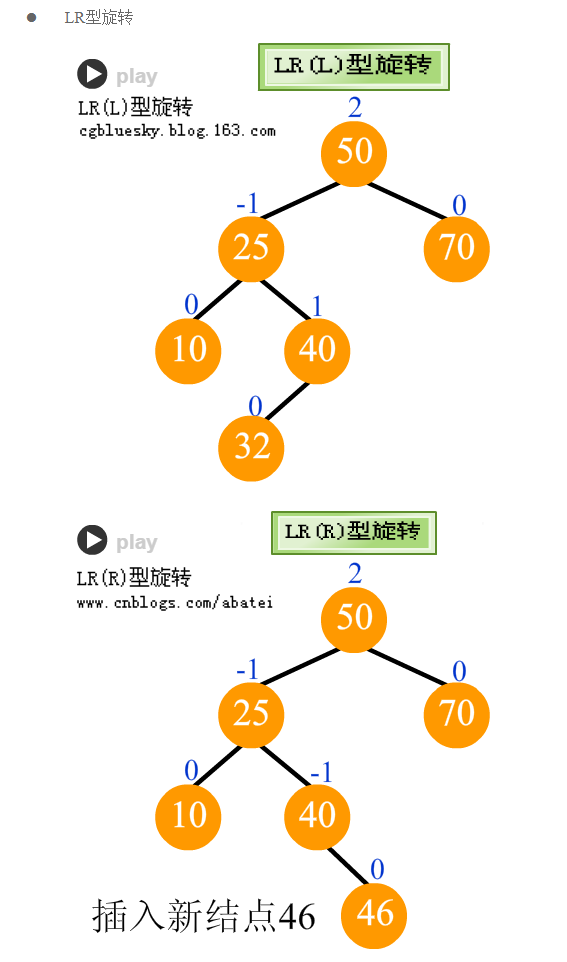
2、左右情况。一是左右左,二是左右右。

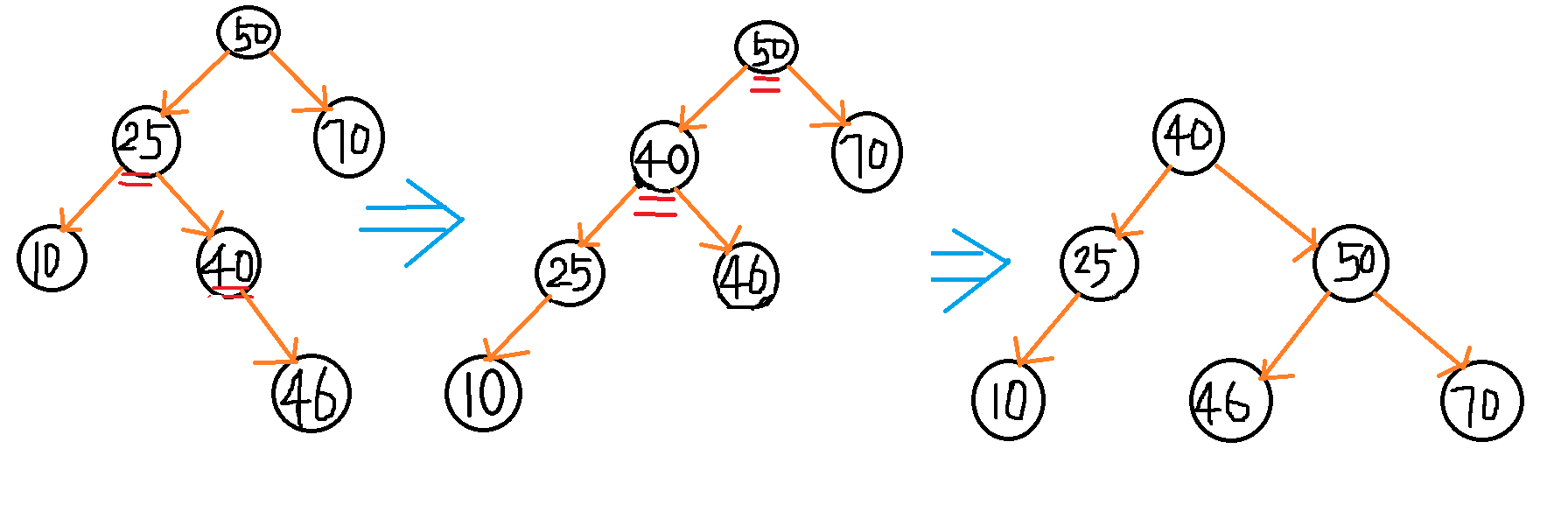
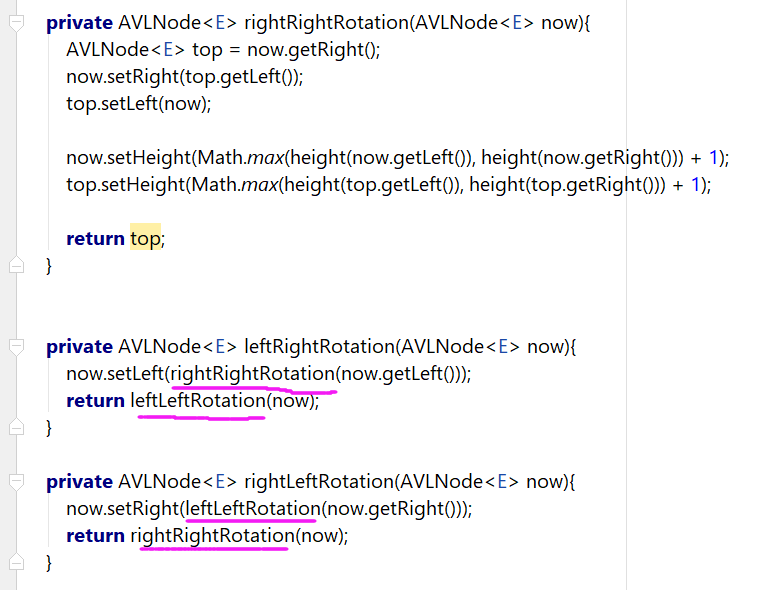
3、RR的情况。
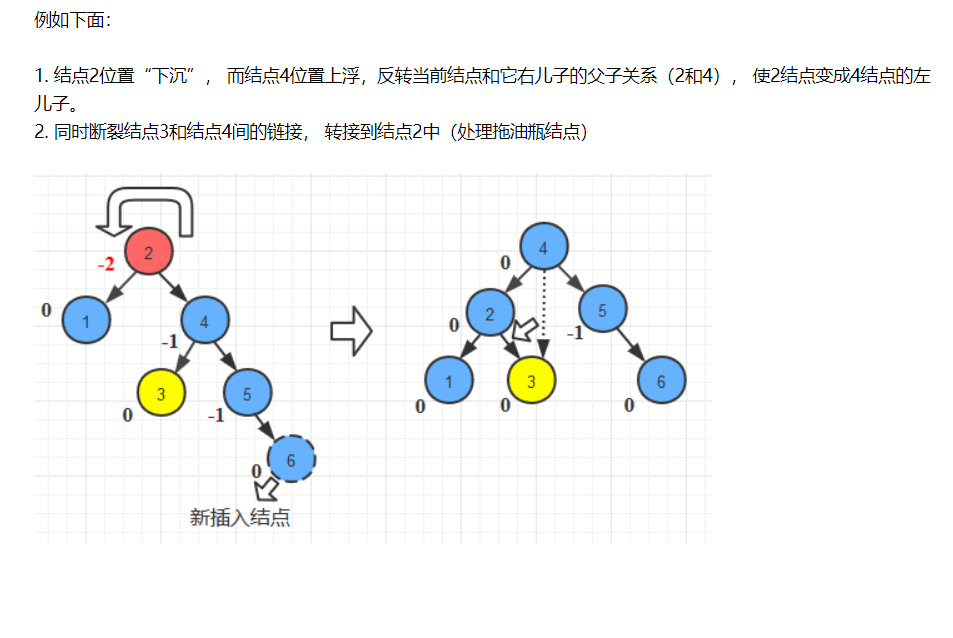
4、右左情况:一是右左左,二是右左右。以下分别是第一、第二种情况,可以合并操作。
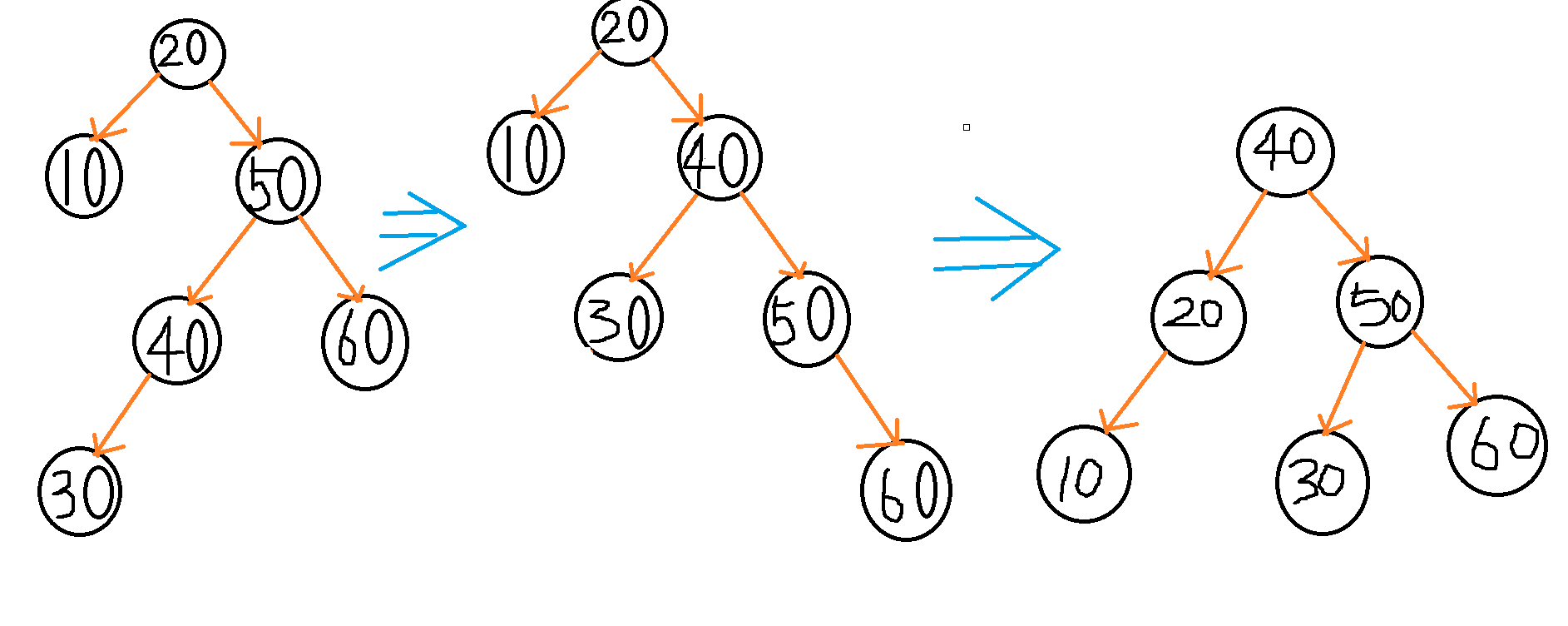
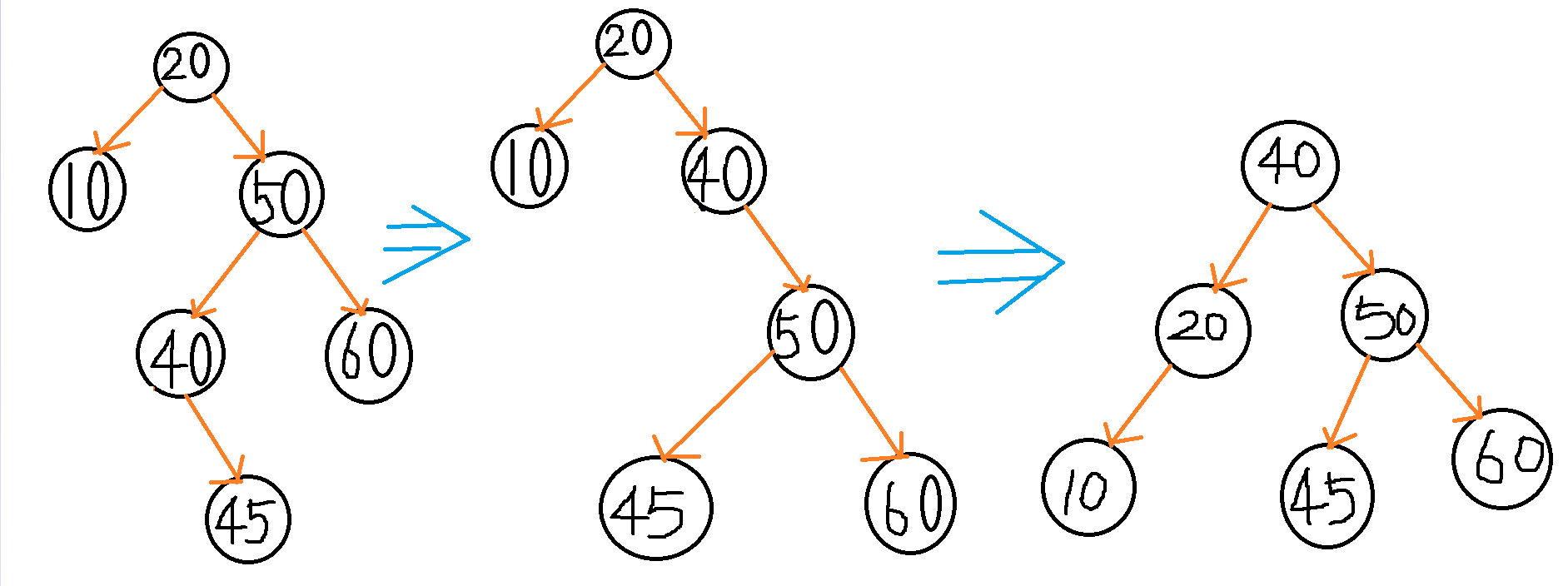
下图的第三个树有一个地方画错了,节点45应该是节点20的右孩子,而图中画成节点50的左孩子了。
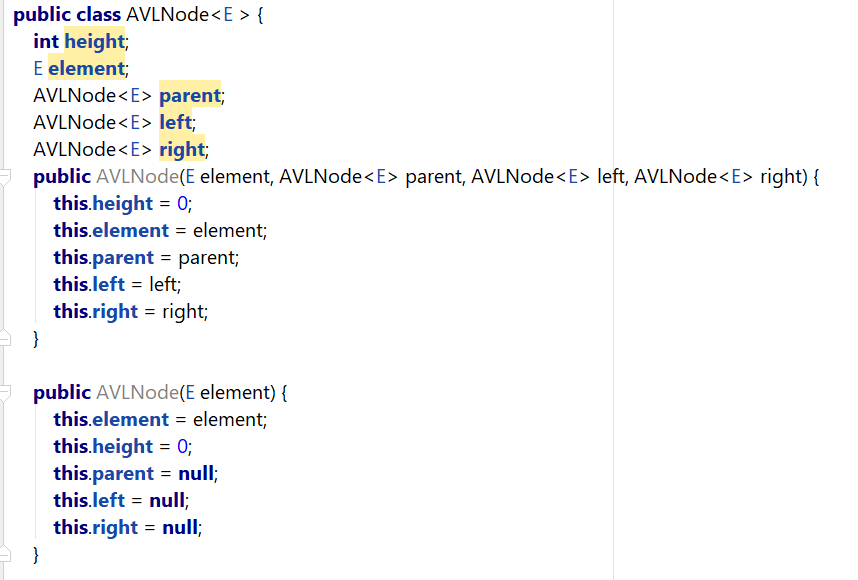
代码分析:节点信息如下:其中parent成员是多余的,可以去掉。
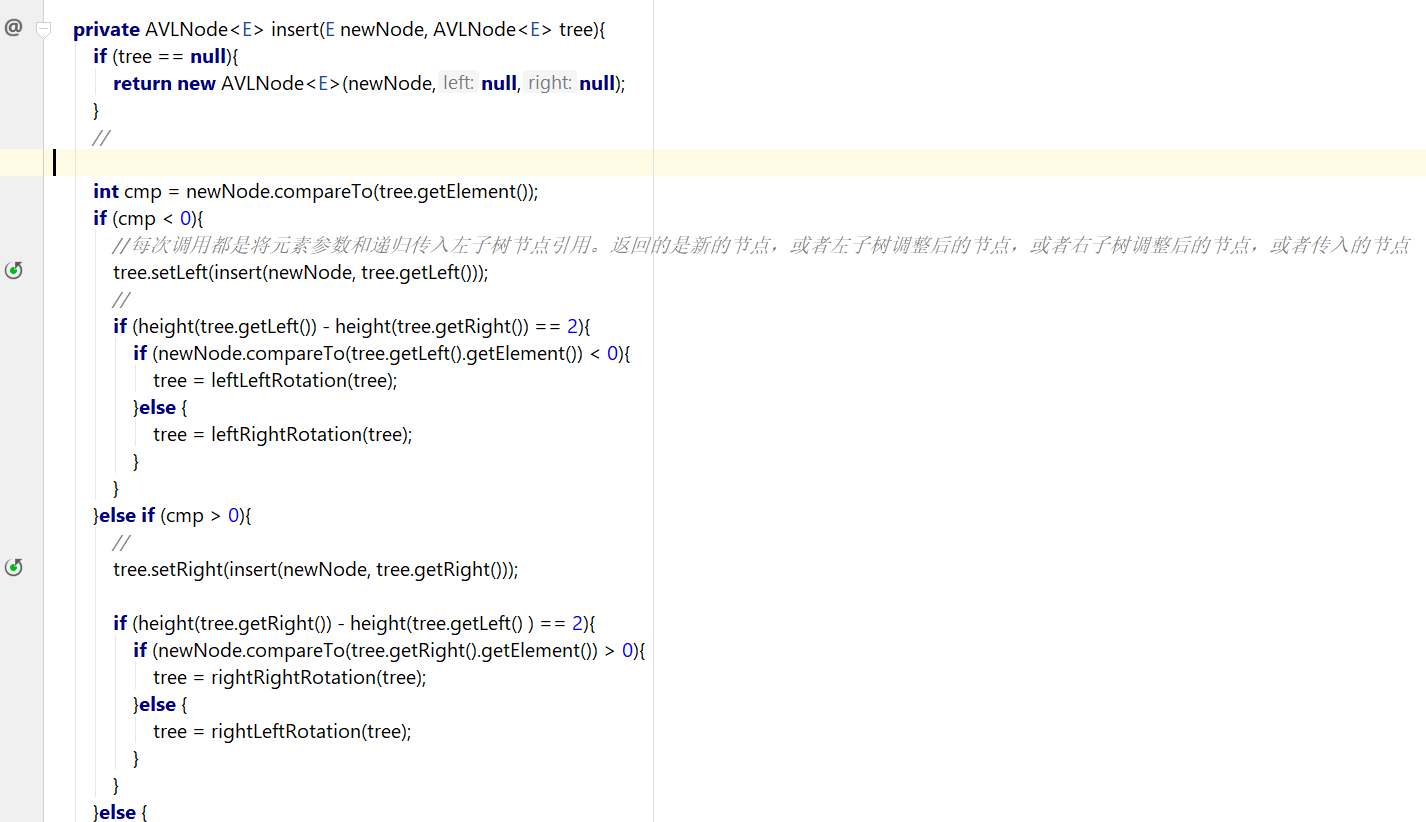
思路:递归找到插入点,并插入节点。再原路返回根节点过程中判断递归路径中所有节点的左右子树的高度差是否达到2,若达到则根据类型来调整,并更新路径中所有节点的高度。
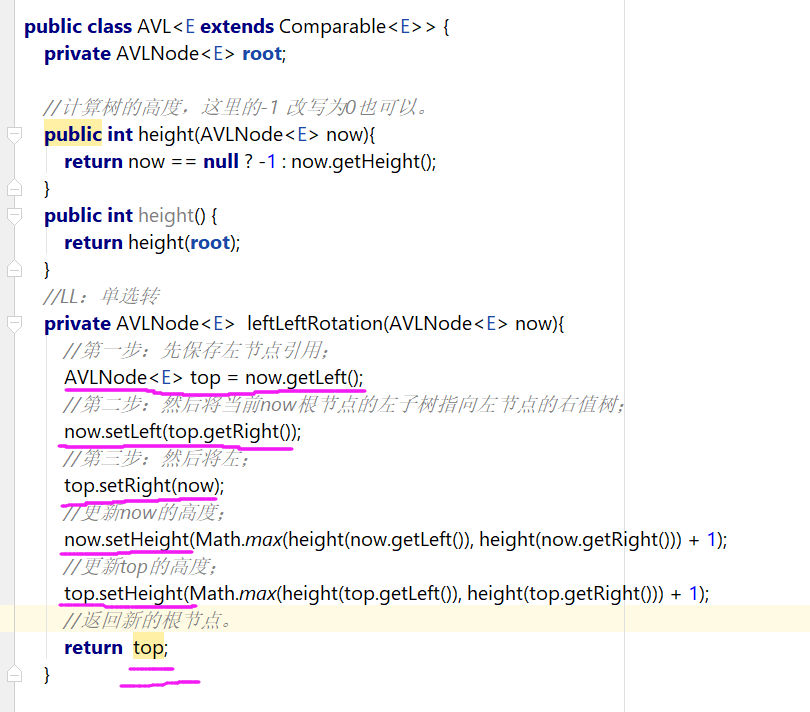
LL旋转代码如下:

一、思想:分类讨论
二、二叉搜索树的删除操作具体讨论分如下四种情况:(记我们要删除的节点为D)
1、如果D节点既没有左孩子,也没有右孩子,那么直接删除就好了;
2、如果D节点只有左孩子,没有右孩子,那么只需要把该D节点左孩子链接到D节点的父亲节点,然后删除D节点就好了;
3、如果D节点只有右孩子,没有左孩子,那么只需要把该D节点右孩子链接到D节点的父亲节点,然后删除D节点就好了;
4、如果D节点既有左孩子,又有右孩子,那么需要找到D节点的右子树的最小值节点,找到之后直接替换掉D节点,然后删除找到的最小值节点就好了。(解释:因为D节点有左右两个孩子节点,很显然D节点的左子树中的所有节点值都小于D节点的值,D节点的右子树中的所有节点的值都大于D节点的值,这个是根据二叉搜索树的定义得到的结论。那么现在D要被删除,那么D被删除之后谁可以来替换它的位置呢?显然只能是D的右子树的最小值可以胜任,因为它既满足大于D节点的左子树中的所有节点值,因为D的右子树的所有节点值都大于D的左子树的节点值;同时也满足小于D的右子树中所有的其他节点值,因为D是右子树中最小的值,当然小于D的右子树中所有其他节点值了)
三、图例说明:
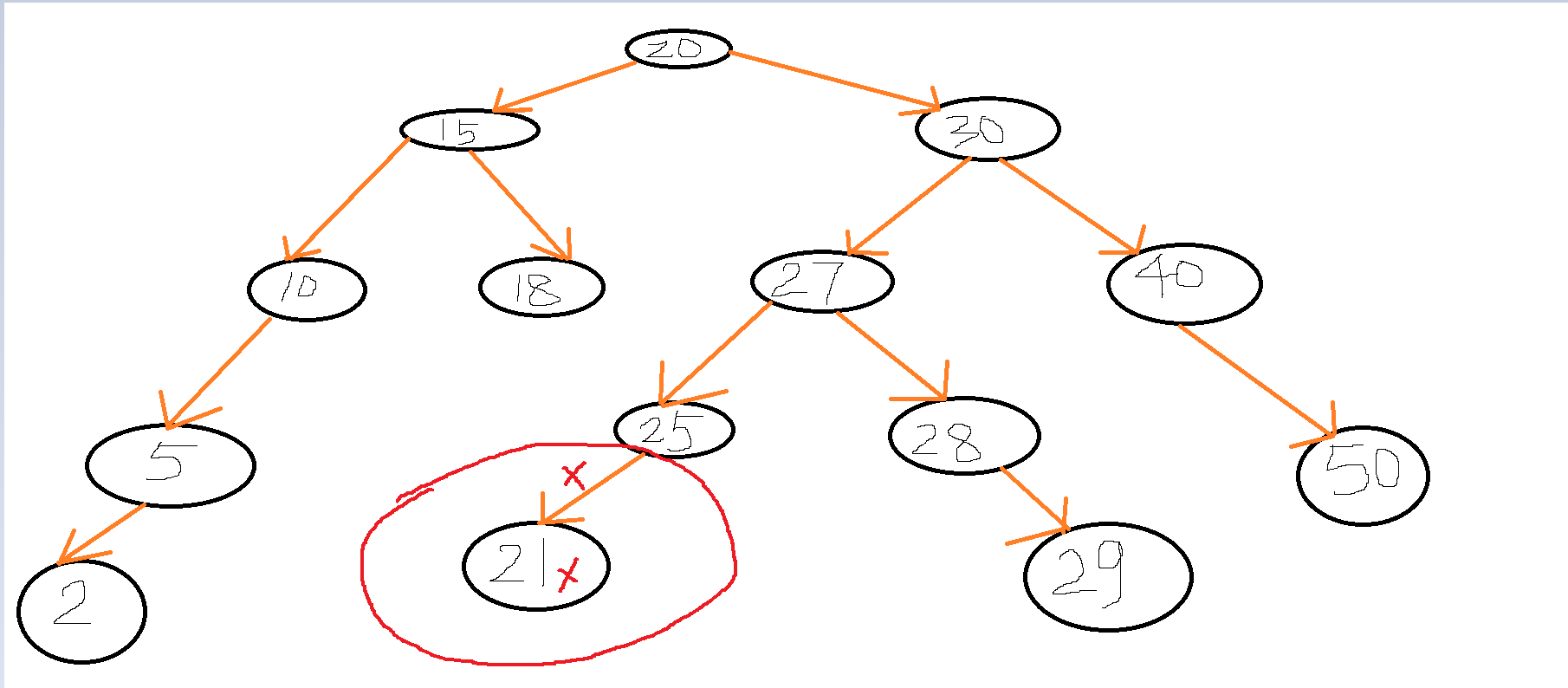
1、第一种情况:这种情况其实就是叶子节点的删除,反正它绝代了,删除了就删除了,多他不多,少它不少。比如删除下图中的21号元素,它既没有左孩子,也没有右孩子,直接将其父节点指向它的链接删除就行了。
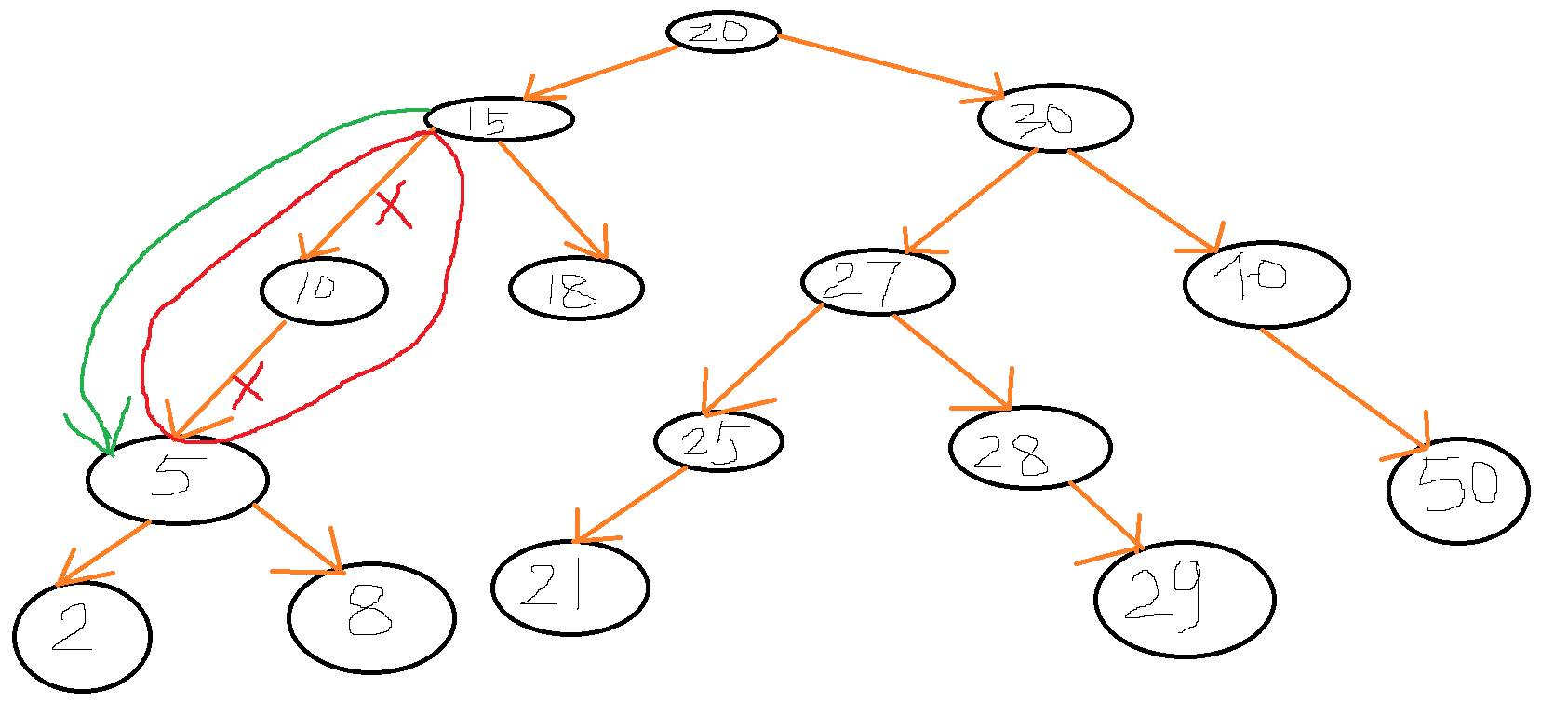
2、第二种情况:删除10号节点,该节点只有左孩子,没有右孩子。只需要三步即可,删除10号节点指向其5号左子树的链接,删除10号节点的父节点15号指向她的链接,将10号节点的父节点15号的左链接指向10号的5号左子树。
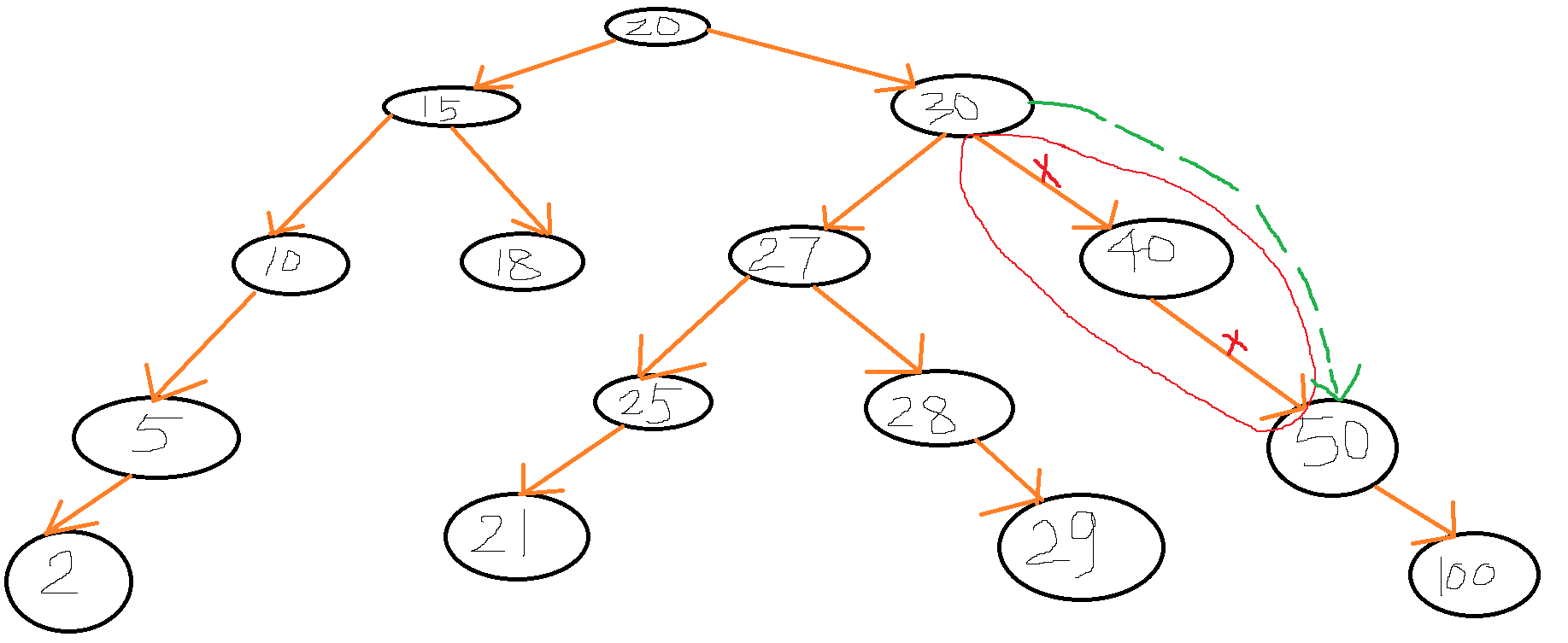
3、第三种情况:删除40号节点,该节点只有右孩子,没有左孩子。只需要三步即可,删除40号节点指向其50号右子树的链接,删除40号节点的父节点30号指向她的链接,将40号节点的父节点30号的右链接指向40号的50号右子树。
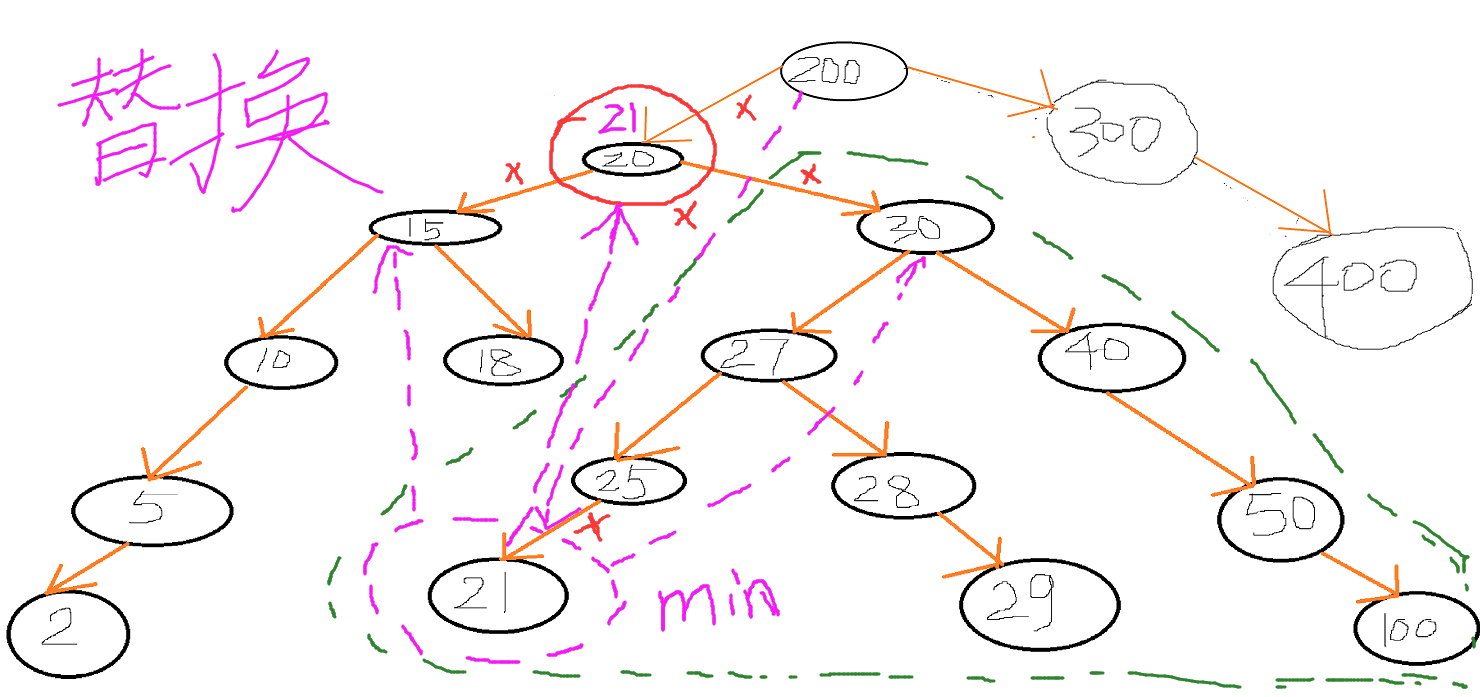
4、第四种情况:删除20号节点,因为他既有左孩子,又有右孩子。所以先找到20号节点的右子树中所有节点中的最小值为21号,其实右子树的最小值就是在右子树的最左边的那个节点;找到替换节点21号后就可以进行下一步操作了,如下图,20号需的父节点指向的链接改变为指向21号,20的左右孩子链接也需要替换,21号原来的父节点指向需要删除。
当然了,还可以找出30号的左子树中的所有节点的最大值来替换该20号节点。方法差不多,要替换一个节点,就去找左子树中最靠近他的节点,或者到他的右子树中最靠近他的节点,其实就是节点的前驱节点和后驱节点。
这里需要了解两个概念,叫“前驱”和“后继”。分别是树中小于它的最大值和大于它的最小值,如果把树结构中的所有节点按顺序拍好的话,它的前驱和它的后继两个节点刚好在它左右紧挨着它。当一个节点被删除时,为了保证二叉树的结构不被破坏,要让它的前驱或者后继节点来代替它的位置,然后将它的前驱或者后继节点同样做删除操作。
那么怎样找前驱或者后继呢。小于它的最大值,就是在树中在它左子树中最靠右的那个节点。同样,大于它的最小值,就是在它右子树中最靠左的那个节点。当一个节点既有左子节点又有右子节点时,前驱就是它的左子节点的右子节点的右子节点...直到最右子节点;后继就是它的右子节点的左子节点的左子节点...直到最左子节点。