2017-2018-1 20162316刘诚昊 实验四 图与应用
20162316刘诚昊 2017-2018-2 《Java程序设计》第四次实验 图的实现与应用
实验链接:
实验四 图的实现与应用-1:
实验要求:
用邻接矩阵实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
实验过程:
参考资料:
http://blog.csdn.net/kelvinmao/article/details/51519284
http://blog.csdn.net/liangxiamoyi/article/details/52153972
构造方法如下:
我将图的点的上限设置为100个。
public Graph_Matrix(){
graphSize = 0;
vertexkist = new String[graphSize];
this.edge=new int[100][100];
}
然后插入与删除节点:
//插入顶点,返回其在顶点顺序表中的下标
public int insertVertex(T x){
//当创建的顶点顺序表长度不够,扩增
this.graphSize++;
if(graphSize == MAXGRAPHSIZE){
MAXGRAPHSIZE = MAXGRAPHSIZE *2;
Object[] N = new Object[MAXGRAPHSIZE];
int a = 0;
for(Object element : vertexkist){
N[a] = element;
a++;
}
vertexkist = N;
}
vertexkist[graphSize - 1] = x;
for(int i=0;i<this.graphSize;i++){
this.edge[i][graphSize-1]=0;
}
for(int i=0;i<this.graphSize;i++){
this.edge[graphSize-1][i]=0;
}
this.edge[graphSize-1][graphSize-1]=0;
return (graphSize);
}
//删除顶点
public void removeVertex(int v) {
if(v>=this.graphSize){
System.out.println("无此顶点");
return;
}
for(int a = v;a<graphSize;a++){
vertexkist[a] = vertexkist[a+1];
}
vertexkist[graphSize-1] = null;
for(int i=0;i<this.graphSize;i++){
this.edge[v][i]=0;
this.edge[i][v]=0;
}
if(v==this.graphSize-1){
this.graphSize--;
return;
}
for(int i=v+1;i<this.graphSize;i++){
for(int j=0;j<this.graphSize;j++){
this.edge[i-1][j]=this.edge[i][j];
}
}
this.graphSize--;
}
边的方面:
//添加边
public void insertEdge(int v1,int v2) throws ElementNotFoundException {
if(v1==v2||v1>this.graphSize||v2>this.graphSize||this.edge[v1][v2]!=0) {
throw new ElementNotFoundException ("插入失败 "
+ "参数错误");
}
this.edge[v1][v2]=1;
System.out.println("添加边成功");
return;
}
//删除边
public void deleteEdge(int v1,int v2) throws ElementNotFoundException {
if(v1==v2||v1>this.graphSize||v2>this.graphSize||this.edge[v1][v2]==0) {
throw new ElementNotFoundException ("插入失败 "
+ "参数错误");
}
this.edge[v1][v2]=0;
System.out.println("删除边成功");
return;
}
遍历方法:
//深度遍历
public void DFS(){
boolean[] visited = new boolean[graphSize];
DFSafter(0,visited);
}
void DFSafter(int k,boolean visited[]){
int u;
System.out.print(vertexkist[k]+", ");
visited[k]=true;
u=GetFirst(k);
while(u!=-1) {
if (visited[u] != true) { /
DFSafter(u, visited);
}
u = GetNext(k, u);
}
}
//广度遍历
public void BFS(int v,int[] visited) {
Queue<Integer> queue = new LinkedList<>();
int next;
queue.add(v);
visited[v]=1;
while (!queue.isEmpty()) {
next=queue.remove();
System.out.print(next + ", ");
int vex = GetFirst(next);
while (vex!=-1) {
if (visited[vex]==0) {
queue.add(vex);
visited[vex]=1;
}
vex=GetNext(next, vex);
}
}
}
另外两个方法很基础且多次练习便不再赘述。
测试截图:
实验四 查找与排序-1代码链接:
点此返回目录
实验四 图的实现与应用-2:
实验要求:
用十字链表实现无向图(边和顶点都要保存),实现在包含添加和删除结点的方法,添加和删除边的方法,size(),isEmpty(),广度优先迭代器,深度优先迭代器
给出伪代码,产品代码,测试代码(不少于5条测试)
实验过程:
参考资料:
http://blog.csdn.net/gongchuangsu/article/details/50866436
十字链表是有向线构成,参考了网上的代码但还是没能做出无向图,最终版本是有向的。
- 节点类:
private class VertexNode {
char vertex;
EdgeNode firstIn;
EdgeNode firstOut;
}
private class EdgeNode {
int tailvex;
int headvex;
EdgeNode headlink;
EdgeNode taillink;
}
- 边与点的操作:
public int insertVertex(char data){
vlen++;
if (ver.length == 0){
ver = new char[1];
}
if(vlen == ver.length) {
int num = ver.length * 2;
char[] n = new char[num];
int b =0;
for (char element : ver){
n[b] = element;
b++;
}
ver = n;
}
ver[ver.length-1] = data;
return vlen;
}
public void inserEdge(int a,int b){
char[][] OLD = edges;
char[][] NEW = new char[OLD.length+1][OLD.length+1];
int c = 0;
for(char[] element:edges){
NEW[c] = element;
}
edges = NEW;
OListDG(ver,edges);
}
public void OListDG(char[] vexs, char[][] edges) {
vlen = vexs.length;
elen = edges.length;
// 初始化顶点,建立顶点表
vertexNodeList = new VertexNode[vlen];
for (int i = 0; i < vlen; i++) {
vertexNodeList[i] = new VertexNode();
vertexNodeList[i].vertex = vexs[i];
vertexNodeList[i].firstIn = null;
vertexNodeList[i].firstOut = null;
}
// 初始化边,利用头插法建立十字链表
for (int i = 0; i < elen; i++) {
EdgeNode edgeNode_1 = new EdgeNode();
EdgeNode edgeNode_2 = new EdgeNode();
int vi = getPosition(edges[i][0], vexs);
int vj = getPosition(edges[i][1], vexs);
edgeNode_1.tailvex = vi;
edgeNode_1.headvex = vj;
edgeNode_1.taillink = vertexNodeList[vi].firstOut;
vertexNodeList[vi].firstOut = edgeNode_1;
edgeNode_2.tailvex = vi;
edgeNode_2.headvex = vj;
edgeNode_2.headlink = vertexNodeList[vj].firstIn;
vertexNodeList[vj].firstIn = edgeNode_2;
}
}
- size与isEmpty
public int size()
return vlen;
}
public boolean isEmpty(){
return ver.length == 0;
}
测试截图

实验四 图的实现与应用-2 代码链接:
产品代码:https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp4/Orthogonal.java
点此返回目录
实验四 图的实现与应用-3:
实验要求:
实现PP19.9
给出伪代码,产品代码,测试代码(不少于5条测试)
实验过程:
这个任务的实现我基于该次实验的第一个实验上做出修改,且自动给出从每个点到另一个点的所有情况(包含最短路径与路径的具体步骤),但出了一点问题,还没有找到原因,就是所有的最小权值都是0,不过具体的路径步骤并没有错。
测试截图:
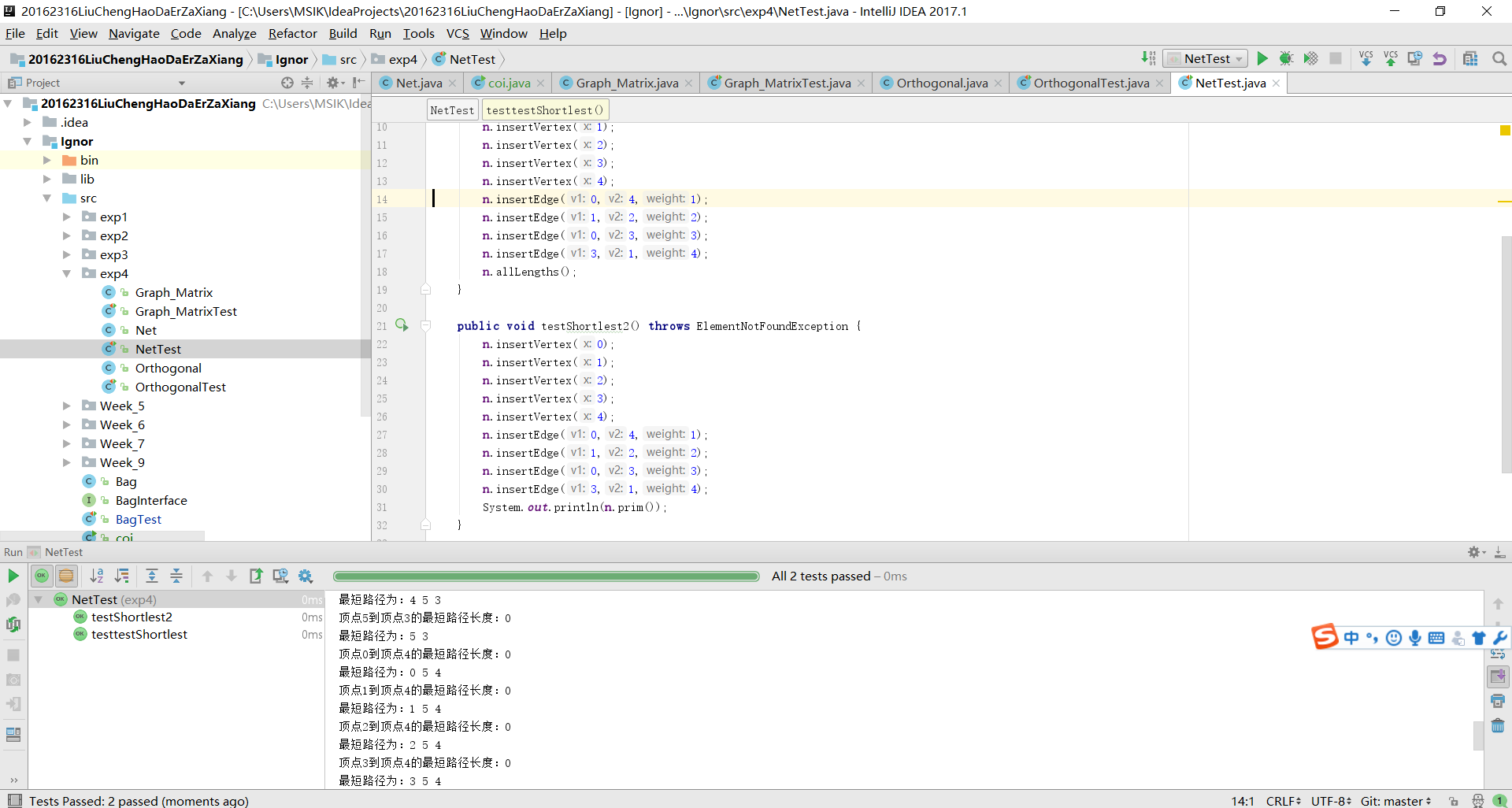
代码链接:
产品代码 https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp4/Net.java
测试代码 https://gitee.com/pdds2017/20162316LiuChengHaoDaErZaXiang/blob/master/Ignor/src/exp4/NetTest.java
点此返回目录



 浙公网安备 33010602011771号
浙公网安备 33010602011771号