LeetCode算法笔记(一)
1.两数之和
暴力法:
class Solution { public int[] twoSum(int[] nums, int target) { for (int i = 0; i < nums.length; i++) { for (int j = i + 1; j < nums.length; j++) { if (nums[j] == target - nums[i]) { return new int[] { i, j }; } } } throw new IllegalArgumentException("No two sum solution"); } }
两遍哈希表
class Solution {
public int[] twoSum(int[] nums, int target) { Map<Integer, Integer> map = new HashMap<>(); for (int i = 0; i < nums.length; i++) { map.put(nums[i], i); } for (int i = 0; i < nums.length; i++) { int complement = target - nums[i]; if (map.containsKey(complement) && map.get(complement) != i) { return new int[] { i, map.get(complement) }; } } throw new IllegalArgumentException("No two sum solution"); } }
一遍哈希表
class Solution { public int[] twoSum(int[] nums, int target) { Map<Integer, Integer> map = new HashMap<>(); for (int i = 0; i < nums.length; i++) { int complement = target - nums[i]; if (map.containsKey(complement)) { return new int[] { map.get(complement), i }; } map.put(nums[i], i); } throw new IllegalArgumentException("No two sum solution"); } }
2.两数之和
给出两个 非空 的链表用来表示两个非负的整数。其中,它们各自的位数是按照 逆序 的方式存储的,并且它们的每个节点只能存储 一位 数字。
如果,我们将这两个数相加起来,则会返回一个新的链表来表示它们的和。假设除了数字 0 之外,这两个数都不会以 0 开头。
public ListNode addTwoNumbers(ListNode l1, ListNode l2) { ListNode dummyHead = new ListNode(0); ListNode p = l1, q = l2, curr = dummyHead; int carry = 0; while (p != null || q != null) { int x = (p != null) ? p.val : 0; int y = (q != null) ? q.val : 0; int sum = carry + x + y; carry = sum / 10; curr.next = new ListNode(sum % 10); curr = curr.next; if (p != null) p = p.next; if (q != null) q = q.next; } if (carry > 0) { curr.next = new ListNode(carry); } return dummyHead.next; }
这里用到了一个链表游标的功能。
3.字符串相乘
给定两个以字符串形式表示的非负整数 num1 和 num2,返回 num1 和 num2 的乘积,它们的乘积也表示为字符串形式。
class Solution { public String multiply(String num1, String num2) { /** num1的第i位(高位从0开始)和num2的第j位相乘的结果在乘积中的位置是[i+j, i+j+1] 例: 123 * 45, 123的第1位 2 和45的第0位 4 乘积 08 存放在结果的第[1, 2]位中 index: 0 1 2 3 4 1 2 3 * 4 5 --------- 1 5 1 0 0 5 --------- 0 6 1 5 1 2 0 8 0 4 --------- 0 5 5 3 5 这样我们就可以单独都对每一位进行相乘计算把结果存入相应的index中 **/ int n1 = num1.length()-1; int n2 = num2.length()-1; if(n1 < 0 || n2 < 0) return ""; int[] mul = new int[n1+n2+2]; for(int i = n1; i >= 0; --i) { for(int j = n2; j >= 0; --j) { int bitmul = (num1.charAt(i)-'0') * (num2.charAt(j)-'0'); bitmul += mul[i+j+1]; // 先加低位判断是否有新的进位 mul[i+j] += bitmul / 10; mul[i+j+1] = bitmul % 10; } } StringBuilder sb = new StringBuilder(); int i = 0; // 去掉前导0 while(i < mul.length-1 && mul[i] == 0) i++; for(; i < mul.length; ++i) sb.append(mul[i]); return sb.toString(); } }
4.无重复字符的最长字串
给定一个字符串,请你找出其中不含有重复字符的 最长子串 的长度。
暴力法:
思路:逐个检查所有的子字符串,看它是否不含有重复的字符。
算法:假设我们有一个函数 boolean allUnique(String substring) ,如果子字符串中的字符都是唯一的,它会返回 true,否则会返回 false。 我们可以遍历给定字符串 s 的所有可能的子字符串并调用函数 allUnique。 如果事实证明返回值为 true,那么我们将会更新无重复字符子串的最大长度的答案。
现在让我们填补缺少的部分:
1.为了枚举给定字符串的所有子字符串,我们需要枚举它们开始和结束的索引。假设开始和结束的索引分别为 i 和 j。那么我们有0≤i<j≤n(这里的结束索引 j 是按惯例排除的)。因此,使用 i 从 0 到 n - 1以及 j从 i+1到 n这两个嵌套的循环,我们可以枚举出 s 的所有子字符串。
2.要检查一个字符串是否有重复字符,我们可以使用集合。我们遍历字符串中的所有字符,并将它们逐个放入 set 中。在放置一个字符之前,我们检查该集合是否已经包含它。如果包含,我们会返回 false。循环结束后,我们返回 true。
public class Solution { public int lengthOfLongestSubstring(String s) { int n = s.length(); int ans = 0; for (int i = 0; i < n; i++) for (int j = i + 1; j <= n; j++) if (allUnique(s, i, j)) ans = Math.max(ans, j - i); return ans; } public boolean allUnique(String s, int start, int end) { Set<Character> set = new HashSet<>(); for (int i = start; i < end; i++) { Character ch = s.charAt(i); if (set.contains(ch)) return false; set.add(ch); } return true; } }
解题思路:考虑使用滑动窗口方法,通过使用 HashSet 作为滑动窗口,我们可以用 O(1)的时间来完成对字符是否在当前的子字符串中的检查。
滑动窗口是数组/字符串问题中常用的抽象概念。 窗口通常是在数组/字符串中由开始和结束索引定义的一系列元素的集合,即 [i, j)左闭,右开)。而滑动窗口是可以将两个边界向某一方向“滑动”的窗口。例如,我们将 [i, j)向右滑动 1 个元素,则它将变为 [i+1, j+1)(左闭,右开)。
回到我们的问题,我们使用 HashSet 将字符存储在当前窗口 [i, j)(最初 j = i)中。 然后我们向右侧滑动索引 j,如果它不在 HashSet 中,我们会继续滑动 j。直到 s[j] 已经存在于 HashSet 中。此时,我们找到的没有重复字符的最长子字符串将会以索引 i 开头。如果我们对所有的 i这样做,就可以得到答案。
public class Solution { public int lengthOfLongestSubstring(String s) { int n = s.length(); Set<Character> set = new HashSet<>(); int ans = 0, i = 0, j = 0; while (i < n && j < n) { // try to extend the range [i, j] if (!set.contains(s.charAt(j))){ set.add(s.charAt(j++)); ans = Math.max(ans, j - i); } else { set.remove(s.charAt(i++)); } } return ans; } }
优化的滑动窗口
上述的方法最多需要执行 2n 个步骤。事实上,它可以被进一步优化为仅需要 n 个步骤。我们可以定义字符到索引的映射,而不是使用集合来判断一个字符是否存在。 当我们找到重复的字符时,我们可以立即跳过该窗口。也就是说,如果 s[j] 在 [i, j)范围内有与 j'重复的字符,我们不需要逐渐增加 i 。 我们可以直接跳过 [i,j'] 范围内的所有元素,并将 i 变为 j' + 1
public class Solution { public int lengthOfLongestSubstring(String s) { int n = s.length(), ans = 0; Map<Character, Integer> map = new HashMap<>(); // current index of character // try to extend the range [i, j] for (int j = 0, i = 0; j < n; j++) { if (map.containsKey(s.charAt(j))) { i = Math.max(map.get(s.charAt(j)), i); } ans = Math.max(ans, j - i + 1); map.put(s.charAt(j), j + 1); } return ans; } }
扩展:Java(假设字符集为 ASCII 128)
以前的我们都没有对字符串 s 所使用的字符集进行假设。
当我们知道该字符集比较小的时侯,我们可以用一个整数数组作为直接访问表来替换 Map。
常用的表如下所示:
- int [26] 用于字母 ‘a’ - ‘z’ 或 ‘A’ - ‘Z’
- int [128] 用于ASCII码
- int [256] 用于扩展ASCII码
public class Solution { public int lengthOfLongestSubstring(String s) { int n = s.length(), ans = 0; int[] index = new int[128]; // current index of character // try to extend the range [i, j] for (int j = 0, i = 0; j < n; j++) { i = Math.max(index[s.charAt(j)], i); ans = Math.max(ans, j - i + 1); index[s.charAt(j)] = j + 1; } return ans; } }
5.寻找两个有序数组的中位数
给定两个大小为 m 和 n 的有序数组 nums1 和 nums2。
请你找出这两个有序数组的中位数,并且要求算法的时间复杂度为 O(log(m + n))。
你可以假设 nums1 和 nums2 不会同时为空。
方:创建一个数组长度为mid+1的数组nums,如果两个数组的长度为偶数,则结果为(nums[mid-1]+nums[mid])/2,如果两个数组的长度为奇数,则结果为nums[mid];
nums数组创建的思路:比较两个数组,按照从小到大的顺序排列。
class Solution { public double findMedianSortedArrays(int[] nums1, int[] nums2) { int len = nums1.length + nums2.length; int mid = len/2; int flag = 0; if(len%2==0){ flag = 1; } int[] nums = new int[mid + 1]; int i = 0, j = 0; for(int k = 0;k < mid+1; k++){ if(i < nums1.length && j < nums2.length){ nums[k] = nums1[i] < nums2[j]? nums1[i++]: nums2[j++]; }else if(i < nums1.length && j >= nums2.length){ nums[k] = nums1[i++]; }else if(j < nums2.length && i >= nums1.length){ nums[k] = nums2[j++]; } } if(flag > 0){ return (nums[mid-1] + nums[mid]) / 2.0; } return nums[mid]; } }
class Solution { public double findMedianSortedArrays(int[] A, int[] B) { int m = A.length; int n = B.length; if (m > n) { // to ensure m<=n int[] temp = A; A = B; B = temp; int tmp = m; m = n; n = tmp; } int iMin = 0, iMax = m, halfLen = (m + n + 1) / 2; while (iMin <= iMax) { int i = (iMin + iMax) / 2; int j = halfLen - i; if (i < iMax && B[j-1] > A[i]){ iMin = i + 1; // i is too small } else if (i > iMin && A[i-1] > B[j]) { iMax = i - 1; // i is too big } else { // i is perfect int maxLeft = 0; if (i == 0) { maxLeft = B[j-1]; } else if (j == 0) { maxLeft = A[i-1]; } else { maxLeft = Math.max(A[i-1], B[j-1]); } if ( (m + n) % 2 == 1 ) { return maxLeft; } int minRight = 0; if (i == m) { minRight = B[j]; } else if (j == n) { minRight = A[i]; } else { minRight = Math.min(B[j], A[i]); } return (maxLeft + minRight) / 2.0; } } return 0.0; } }
6.最长回文子串
给定一个字符串 s,找到 s 中最长的回文子串。你可以假设 s 的最大长度为 1000。
方:这里使用窗口滑动方法,求最长回文,窗口大小考虑从大到小设置,首先让窗口大小设置为s.length(),逐个比较两边元素是否相等。
class Solution { public String longestPalindrome(String s) { if(s.length() == 1 || "".equals(s)) return s; int len = s.length(); int subLen = len; while(subLen>0){ for(int i = 0; i + subLen <= len; i++){ String subStr = s.substring(i, i + subLen); int midLen = (subLen + 1) / 2; for(int k = 0; k < midLen; k++){ if(subStr.charAt(k) != subStr.charAt(subLen - k - 1)){ break; } if(k == midLen-1){ return subStr; } } } subLen--; } return ""; } }
扩展中心法:
public String longestPalindrome(String s) { if (s == null || s.length() < 1) return ""; int start = 0, end = 0; for (int i = 0; i < s.length(); i++) { int len1 = expandAroundCenter(s, i, i); int len2 = expandAroundCenter(s, i, i + 1); int len = Math.max(len1, len2); if (len > end - start) { start = i - (len - 1) / 2; end = i + len / 2; } } return s.substring(start, end + 1); } private int expandAroundCenter(String s, int left, int right) { int L = left, R = right; while (L >= 0 && R < s.length() && s.charAt(L) == s.charAt(R)) { L--; R++; } return R - L - 1;//这里-1是因为这个时候的R和L超出了回文的范围,且这个时候已经不是回文了 }
public String Manacher(String s) { if (s.length() < 2) { return s; } StringBuilder sb = new StringBuilder(); sb.append("^"); for(int i=0; i < s.length(); i++){ sb.append("#" + s.charAt(i)); } sb.append("#$"); String t = sb.toString(); int len = t.length(); int[] p = new int[len]; int mx = 0, id = 0, maxLength=-1; int index = 0; for(int i = 1; i < len - 1; i++){ p[i] = mx > i? Math.min(p[2*id-i], mx-i):1; while(t.charAt(i + p[i]) == t.charAt(i - p[i])){ p[i]++; } if(mx < i + p[i]){ mx = i + p[i]; id = i; } if(maxLength < p[i] - 1 ){ index = i; maxLength = p[i] - 1; } } int start = (index - p[index]) / 2; return s.substring(start, start + maxLength); }
7.Z字形变换
将一个给定字符串根据给定的行数,以从上往下、从左到右进行 Z 字形排列。
思路:通过从左向右迭代字符串,我们可以轻松地确定字符位于 Z 字形图案中的哪一行。
算法:我们可以使用min(numRows,len(s)) 个列表来表示 Z 字形图案中的非空行。
从左到右迭代s,将每个字符添加到合适的行。可以使用当前行和当前方向这两个变量对合适的行进行跟踪。
只有当我们向上移动到最上面的行或向下移动到最下面的行时,当前方向才会发生改变。
public String convert(String s, int numRows) {
if (numRows == 1) return s; List<StringBuilder> rows = new ArrayList<>(); for (int i = 0; i < Math.min(numRows, s.length()); i++) rows.add(new StringBuilder()); int curRow = 0; boolean goingDown = false; for (char c : s.toCharArray()) { rows.get(curRow).append(c); if (curRow == 0 || curRow == numRows - 1) goingDown = !goingDown; curRow += goingDown ? 1 : -1; } StringBuilder ret = new StringBuilder(); for (StringBuilder row : rows) ret.append(row); return ret.toString(); }
思路:按照与逐行读取 Z 字形图案相同的顺序访问字符串。
算法:首先访问 行 0 中的所有字符,接着访问 行 1,然后 行 2,依此类推...
对于所有整数 k,
行 0 中的字符位于索引 k(2⋅numRows−2) 处;
行numRows−1 中的字符位于索引 k(2⋅numRows−2)+numRows−1 处;
内部的 行 i 中的字符位于索引 k(2⋅numRows−2)+i 以及(k+1)(2⋅numRows−2)−i 处;
class Solution {
public String convert(String s, int numRows) { if (numRows == 1) return s; StringBuilder ret = new StringBuilder(); int n = s.length(); int cycleLen = 2 * numRows - 2; for (int i = 0; i < numRows; i++) { for (int j = 0; j + i < n; j += cycleLen) { ret.append(s.charAt(j + i)); if (i != 0 && i != numRows - 1 && j + cycleLen - i < n) ret.append(s.charAt(j + cycleLen - i)); } } return ret.toString(); } }
8.整数反转
给出一个 32 位的有符号整数,你需要将这个整数中每位上的数字进行反转。
注意:假设我们的环境只能存储得下 32 位的有符号整数,则其数值范围为 [−2^31, 2^31 − 1]-->[-2147483648, 2147483647]。请根据这个假设,如果反转后整数溢出那么就返回 0。
该算法定义了一个Long int类型数据,Long是一个64位的整数,因此,可以存放下32位有符号整数。先使用Long存储,最后结果判断范围。
该算法因为定义了一个Long类型,需要占用更多的内存。
public int reverse(int x) { Long result = 0L ; for(;x!=0;x=x/10){ result = result*10+x%10; } return result>Integer.MAX_VALUE || result<Integer.MIN_VALUE? 0:result.intValue();//转换为int型
}
这里将int先转换为String类型,且会判断正负和最后一位是否为0;判断方法是取出String中的char字符,并进行比较。String-->StringBuilder,reverse()-->int.
此时可能会转换出错,因为超出int范围,这里我用try-catch进行回传,这种算法不合适
public int reverse(int x){ if(x < 10 && x > -10) return x; String result = String.valueOf(x); boolean fu = false; if(result.charAt(0) == '-'){ fu = true; result = result.substring(1); } if(result.charAt(result.length() - 1) == '0'){ result = result.substring(0, result.length() - 1); } StringBuilder sb = new StringBuilder(result); sb = sb.reverse(); result = sb.toString(); if(fu){ try{ return -Integer.parseInt(result); }catch(Exception e){ return 0; } } try{ return Integer.parseInt(result); }catch(Exception e){ return 0; } }
方法:弹出和推入数字 & 溢出前进行检查
思路:我们可以一次构建反转整数的一位数字。在这样做的时候,我们可以预先检查向原整数附加另一位数字是否会导致溢出。
算法:反转整数的方法可以与反转字符串进行类比。
我们想重复“弹出”xx 的最后一位数字,并将它“推入”到rev 的后面。最后,rev 将与 x相反。
要在没有辅助堆栈/数组的帮助下 “弹出” 和 “推入” 数字,我们可以使用数学方法。
//pop operation: pop = x % 10; x /= 10; //push operation: temp = rev * 10 + pop; rev = temp;
但是,这种方法很危险,因为当 temp=rev⋅10+pop 时会导致溢出。
幸运的是,事先检查这个语句是否会导致溢出很容易。
为了便于解释,我们假设rev 是正数。
如果temp=rev⋅10+pop 导致溢出,那么一定有rev≥ INTMAX /10 。 如果rev> INTMAX/10,那么 temp=rev⋅10+pop 一定会溢出。 如果rev== INTMAX/10,那么只要pop > 7, temp=rev⋅10+pop 就会溢出。
当rev 为负时可以应用类似的逻辑。
class Solution {
public int reverse(int x) {
int rev = 0; while (x != 0) { int pop = x % 10; x /= 10; if (rev > Integer.MAX_VALUE/10 || (rev == Integer.MAX_VALUE / 10 && pop > 7)) return 0; if (rev < Integer.MIN_VALUE/10 || (rev == Integer.MIN_VALUE / 10 && pop < -8)) return 0; rev = rev * 10 + pop; } return rev; } }
9.字符串转换整数
实现一个 atoi 函数,使其能将字符串转换成整数。
首先,该函数会根据需要丢弃无用的开头空格字符,直到寻找到第一个非空格的字符为止。
当我们寻找到的第一个非空字符为正或者负号时,则将该符号与之后面尽可能多的连续数字组合起来,作为该整数的正负号;假如第一个非空字符是数字,则直接将其与之后连续的数字字符组合起来,形成整数。
该字符串除了有效的整数部分之后也可能会存在多余的字符,这些字符可以被忽略,它们对于函数不应该造成影响。
注意:假如该字符串中的第一个非空格字符不是一个有效整数字符、字符串为空或字符串仅包含空白字符时,则你的函数不需要进行转换。
在任何情况下,若函数不能进行有效的转换时,请返回 0。
说明:假设我们的环境只能存储 32 位大小的有符号整数,那么其数值范围为 [−2^31, 2^31 − 1]。如果数值超过这个范围,请返回 INT_MAX (231 − 1) 或 INT_MIN (−231) 。
class Solution { public int myAtoi(String str) { str = str.trim();//针对" "这种情况 if("".equals(str)) return 0;//先处理一次空字符串 boolean fu = false; if(str.charAt(0) == '-' || str.charAt(0) == '+') { if(str.charAt(0) == '-') fu = true; str = str.substring(1); } if("".equals(str)) return 0;//针对"-", "+" int k = 0; if(str.charAt(0) > 57 || str.charAt(0) < 48) return 0;//除符号外,如果首字符是字符,则返回0 while(k < str.length()){ if(str.charAt(k) > 57 || str.charAt(k) < 48) break;//先数字,后字符的情况 k++; } str = str.substring(0, k); try{//这里用try-catch处理字符越界的情况 return fu? -Integer.parseInt(str):Integer.parseInt(str); }catch(Exception e){ return fu? Integer.MIN_VALUE: Integer.MAX_VALUE; } } }
public class Solution { public int myAtoi(String str) { int len = str.length(); // 去除前导空格 int index = 0; while (index < len) { if (str.charAt(index) != ' ') { break; } index++; } if (index == len) { return 0; } // 第 1 个字符如果是符号,判断合法性,并记录正负 int sign = 1; char firstChar = str.charAt(index); if (firstChar == '+') { index++; sign = 1; } else if (firstChar == '-') { index++; sign = -1; } // 不能使用 long 类型,这是题目说的 int res = 0; while (index < len) { char currChar = str.charAt(index); // 判断合法性 if (currChar > '9' || currChar < '0') { break; } // 题目中说:环境只能存储 32 位大小的有符号整数,因此,需要提前判断乘以 10 以后是否越界 if (res > Integer.MAX_VALUE / 10 || (res == Integer.MAX_VALUE / 10 && (currChar - '0') > Integer.MAX_VALUE % 10)) { return Integer.MAX_VALUE; } if (res < Integer.MIN_VALUE / 10 || (res == Integer.MIN_VALUE / 10 && (currChar - '0') > -(Integer.MIN_VALUE % 10))) { return Integer.MIN_VALUE; } // 每一步都把符号位乘进去 res = res * 10 + sign * (currChar - '0'); index++; } return res; } }
class Solution { public int myAtoi(String str) { int len = str.length(); int index = 0; while(index < len){ if(str.charAt(index) != ' '){ break; } index++; } if(index == len) return 0; int sign = 1; char firstChar = str.charAt(index); if(firstChar == '-'){ index++; sign = -1; }else if(firstChar == '+'){ index++; sign = 1; } int result = 0; while(index < len){ int pop = str.charAt(index) - '0'; if(pop > 9 || pop < 0) break; if(result > Integer.MAX_VALUE/10 || (result == Integer.MAX_VALUE/10 && pop > Integer.MAX_VALUE % 10)) return Integer.MAX_VALUE; if(result < Integer.MIN_VALUE/10 || (result == Integer.MIN_VALUE/10 && pop > -(Integer.MIN_VALUE % 10))) return Integer.MIN_VALUE; result = result*10 + sign*pop; index++; } return result; } }
10.回文数
判断一个整数是否是回文数。回文数是指正序(从左向右)和倒序(从右向左)读都是一样的整数。
class Solution { public boolean isPalindrome(int x) { if(x < 0 || (x%10==0 && x > 0)) return false; int result = 0; while(x > result){ result = result*10 + x % 10; x /= 10; } return (result == x) || (x == result/10); } }
11.正则表达式匹配
12.盛最多水的容器
给定 n 个非负整数 a1,a2,...,an,每个数代表坐标中的一个点 (i, ai) 。在坐标内画 n 条垂直线,垂直线 i 的两个端点分别为 (i, ai) 和 (i, 0)。找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
说明:你不能倾斜容器,且 n 的值至少为 2。
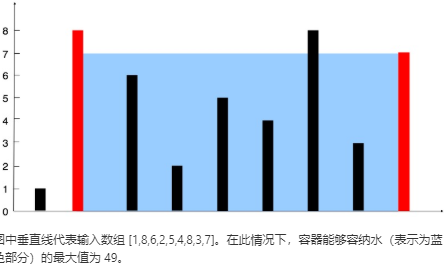
暴力法
class Solution { public int maxArea(int[] height) { if(height.length < 2) return 0; int len = height.length; int maxArea = 0; for(int i = 0; i < len - 1; i++){ for(int j = 0; j < len; j++){ maxArea = Math.max(maxArea, (j - i)*Math.min(height[i], height[j])); } } return maxArea; } }
左右指针法,保留大的指针
class Solution { public int maxArea(int[] height) { int l = 0, maxArea = 0, r = height.length - 1; while(l < r){ maxArea = Math.max(maxArea, (r-l)*Math.min(height[l], height[r])); if(height[l] > height[r]){ r--; }else{ l++; } } return maxArea; } }
左右指针算法,相比上面,多了一个中间指针,优势在于不需要每选择一个区间都进行面积计算,中间指针可以使得只有面积比原来大才进行面积计算。
class Solution { public int maxArea(int[] height) { int l = 0, maxArea = 0, r = height.length - 1, mid=0; while(l < r){ mid = height[l] > height[r]? r: l; maxArea = Math.max(maxArea, (r-l)*Math.min(height[l], height[r])); if(height[l] > height[r]){ r--; while(height[r] <= height[mid]){ r--; if(l >= r){ return maxArea; } } }else { l++; while(height[l] <= height[mid]){ l++; if(l >= r){ return maxArea; } } } } return maxArea; } }
13.整数转罗马数字
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
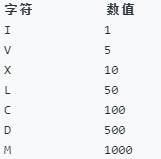
例如, 罗马数字 2 写做 II ,即为两个并列的 1。12 写做 XII ,即为 X + II 。 27 写做 XXVII, 即为 XX + V + II 。
通常情况下,罗马数字中小的数字在大的数字的右边。但也存在特例,例如 4 不写做 IIII,而是 IV。数字 1 在数字 5 的左边,所表示的数等于大数 5 减小数 1 得到的数值 4 。同样地,数字 9 表示为 IX。这个特殊的规则只适用于以下六种情况:
I 可以放在 V (5) 和 X (10) 的左边,来表示 4 和 9。
X 可以放在 L (50) 和 C (100) 的左边,来表示 40 和 90。
C 可以放在 D (500) 和 M (1000) 的左边,来表示 400 和 900。
给定一个整数,将其转为罗马数字。输入确保在 1 到 3999 的范围内。
贪心算法:本题“整数转罗马数字”也有类似的思想:在表示一个较大整数的时候,“罗马数字”的设计者不会让你都用 11 加起来,我们总是希望写出来的“罗马数字”的个数越少越好,以方便表示,并且这种表示方式还应该是唯一的。
class Solution { public String intToRoman(int num) { if(num < 1 || num > 3999) return ""; int[] nums = new int[]{1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1}; String[] roms = new String[]{"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"}; StringBuilder sb = new StringBuilder(); int index = 0; while(index < 13){ while(num >= nums[index]){ sb.append(roms[index]); num -= nums[index]; } index++; } return sb.toString(); } }
暴力法:输入的数据最多4位,创建4个数组,得到每位数字,选择对应的表示形式。
/**if(num < 1 || num > 3999) return ""; int[] nums = new int[]{1000, 900, 500, 400, 100, 90, 50, 40, 10, 9, 5, 4, 1}; String[] roms = new String[]{"M", "CM", "D", "CD", "C", "XC", "L", "XL", "X", "IX", "V", "IV", "I"}; StringBuilder sb = new StringBuilder(); int index = 0; while(index < 13){ while(num >= nums[index]){ sb.append(roms[index]); num -= nums[index]; } index++; } return sb.toString();*/ if(num < 1 || num > 3999) return ""; //String[] zeros = new String[]{"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"}; //String[] ones = new String[]{"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"}; //String[] twos = new String[]{"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"}; //String[] threes = new String[]{"", "M", "MM", "MMM"}; String[][] romans = new String[][]{{"", "I", "II", "III", "IV", "V", "VI", "VII", "VIII", "IX"}, {"", "X", "XX", "XXX", "XL", "L", "LX", "LXX", "LXXX", "XC"}, {"", "C", "CC", "CCC", "CD", "D", "DC", "DCC", "DCCC", "CM"}, {"", "M", "MM", "MMM", "", "", "", "", "", ""}}; //int zero = 0, one = 0, two = 0, three = 0; int pop = 0; StringBuilder sb = new StringBuilder(); for(int i = 0; i < 4; i++){ pop = num % 10; num /= 10; sb.insert(0, romans[i][pop]); } /*zero = num % 10; num /= 10; one = num % 10; num /= 10; two = num %10; num /= 10; three = num % 10; StringBuilder sb = new StringBuilder(); sb.append(threes[three]); sb.append(twos[two]); sb.append(ones[one]); sb.append(zeros[zero]);*/ return sb.toString(); }
14.罗马数字转整数
罗马数字包含以下七种字符: I, V, X, L,C,D 和 M。
字符 数值 I 1 V 5 X 10 L 50 C 100 D 500 M 1000
使用一个map存储所有特殊的罗马数字,逐个读取roman数字,当遇到'C', 'X', 'I'这些可能造成歧义的数字时往后多看一位,并进行判断是否存在于map中。
class Solution { public int romanToInt(String s) { Map<String, Integer> map = new HashMap<>(); map.put("M", 1000); map.put("CM", 900); map.put("D", 500); map.put("CD", 400); map.put("C", 100); map.put("XC", 90); map.put("L", 50); map.put("XL", 40); map.put("X", 10); map.put("IX", 9); map.put("V", 5); map.put("IV", 4); map.put("I", 1); int len = s.length(); int result = 0; for(int i = 0; i < len; i++){ char temp = s.charAt(i); if(i < len -1 && (temp == 'C' || temp == 'X' || temp == 'I')){ String tmp = s.substring(i, i + 2); if(map.containsKey(tmp)){ result += map.get(tmp); i++; }else{ result += map.get(String.valueOf(temp)); } }else{ result += map.get(String.valueOf(temp)); } } return result; } }
该算法在代码实现上,可以往后看多一位,对比当前位与后一位的大小关系,从而确定当前位是加还是减法。当没有下一位时,做加法即可。
也可保留当前位的值,当遍历到下一位的时,对比保留值与遍历位的大小关系,再确定保留值为加还是减。最后一位做加法即可。
class Solution {
public int romanToInt(String s) { int sum = 0; int preNum = getValue(s.charAt(0)); for(int i = 1;i < s.length(); i ++) { int num = getValue(s.charAt(i)); if(preNum < num) { sum -= preNum; } else { sum += preNum; } preNum = num; } sum += preNum; return sum; } private int getValue(char ch) { switch(ch) { case 'I': return 1; case 'V': return 5; case 'X': return 10; case 'L': return 50; case 'C': return 100; case 'D': return 500; case 'M': return 1000; default: return 0; } } }
15.最长公共前缀
编写一个函数来查找字符串数组中的最长公共前缀。
如果不存在公共前缀,返回空字符串 ""。
暴力法:选择字符串数组中首个字符串为比较字符串,逐个提取该字符串的字符,然后与其他字符串进行比较,发现有不相等的马上退出循环。
class Solution { public String longestCommonPrefix(String[] strs) { if(strs.length == 0) return "";//[] if(strs.length == 1) return strs[0];//[""]/["as"] int len = strs.length; for(int i = 0; i < len; i++){//针对字符串数组中出现""字符串的情况 if(strs[i].equals("")) return ""; } int index = 0; boolean end = false; char temp; while(true){ if(index < strs[0].length()){//防止越界 temp = strs[0].charAt(index); }else{ break; } for(int i = 1; i < len; i++){//与剩余的字符串中的字符逐个比较 if(index >= strs[i].length() || strs[i].charAt(index) != temp){ end = true; break; } } if(end) break; index++; } return strs[0].substring(0, index); } }
方法一:水平扫描法 思路:首先,我们将描述一种查找一组字符串的最长公共前缀LCP(S1…Sn) 的简单方法。我们将会用到这样的结论:LCP(S1…Sn)=LCP(LCP(LCP(S1,S2),S3),…Sn) 算法:为了运用这种思想,算法要依次遍历字符串[S1…Sn],当遍历到第 ii 个字符串的时候,找到最长公共前缀LCP(S1…Si)。当LCP(S1…Si) 是一个空串的时候,算法就结束了。
否则,在执行了n次遍历之后,算法就会返回最终答案LCP(S1…Sn)。
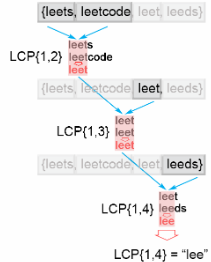
public String longestCommonPrefix(String[] strs) {
if (strs.length == 0) return "";
String prefix = strs[0];
for (int i = 1; i < strs.length; i++)
while (strs[i].indexOf(prefix) != 0) {
prefix = prefix.substring(0, prefix.length() - 1);
if (prefix.isEmpty()) return "";
}
return prefix;
}
算法二:水平扫描
算法:想象数组的末尾有一个非常短的字符串,使用上述方法依旧会进行S次比较。优化这类情况的一种方法就是水平扫描。我们从前往后枚举字符串的每一列,先比较每个字符串相同列上的字符(即不同字符串相同下标的字符)然后再进行对下一列的比较。
public String longestCommonPrefix(String[] strs) { if (strs == null || strs.length == 0) return ""; for (int i = 0; i < strs[0].length() ; i++){ char c = strs[0].charAt(i); for (int j = 1; j < strs.length; j ++) { if (i == strs[j].length() || strs[j].charAt(i) != c) return strs[0].substring(0, i); } } return strs[0]; }
算法三:分治 思路:这个算法的思路来自于LCP操作的结合律。 我们可以发现:LCP(S1…Sn)=LCP(LCP(S1…Sk),LCP(Sk+1…Sn)),其中 LCP(S1…Sn) 是字符串[S1…Sn]的最长公共前缀,1<k<n。
算法:为了应用上述的结论,我们使用分治的技巧,将原问题LCP(Si⋯Sj)分成两个子问题LCP(Si⋯Smid)与LCP(Smid+1,Sj) ,其中 mid=(i+j)/2。
我们用子问题的解 lcpLeft 与 lcpRight 构造原问题的解LCP(Si⋯Sj)。 从头到尾挨个比较 lcpLeft 与 lcpRight 中的字符,直到不能再匹配为止。
计算所得的 lcpLeft 与 lcpRight 最长公共前缀就是原问题的解LCP(Si⋯Sj)。
public String longestCommonPrefix(String[] strs) { if (strs == null || strs.length == 0) return ""; return longestCommonPrefix(strs, 0 , strs.length - 1); } private String longestCommonPrefix(String[] strs, int l, int r) { if (l == r) { return strs[l]; } else { int mid = (l + r)/2; String lcpLeft = longestCommonPrefix(strs, l , mid); String lcpRight = longestCommonPrefix(strs, mid + 1,r); return commonPrefix(lcpLeft, lcpRight); } } String commonPrefix(String left,String right) { int min = Math.min(left.length(), right.length()); for (int i = 0; i < min; i++) { if ( left.charAt(i) != right.charAt(i) ) return left.substring(0, i); } return left.substring(0, min); }
二分查找法:
这个想法是应用二分查找法找到所有字符串的公共前缀的最大长度 L。 算法的查找区间是(0…minLen),其中minLen是输入数据中最短的字符串的长度,同时也是答案的最长可能长度。 每一次将查找区间一分为二,然后丢弃一定不包含最终答案的那一个。算法进行的过程中一共会出现两种可能情况:
S[1...mid] 不是所有串的公共前缀。 这表明对于所有的 j > i S[1..j] 也不是公共前缀,于是我们就可以丢弃后半个查找区间。
S[1...mid] 是所有串的公共前缀。 这表示对于所有的 i < j S[1..i] 都是可行的公共前缀,因为我们要找最长的公共前缀,所以我们可以把前半个查找区间丢弃。
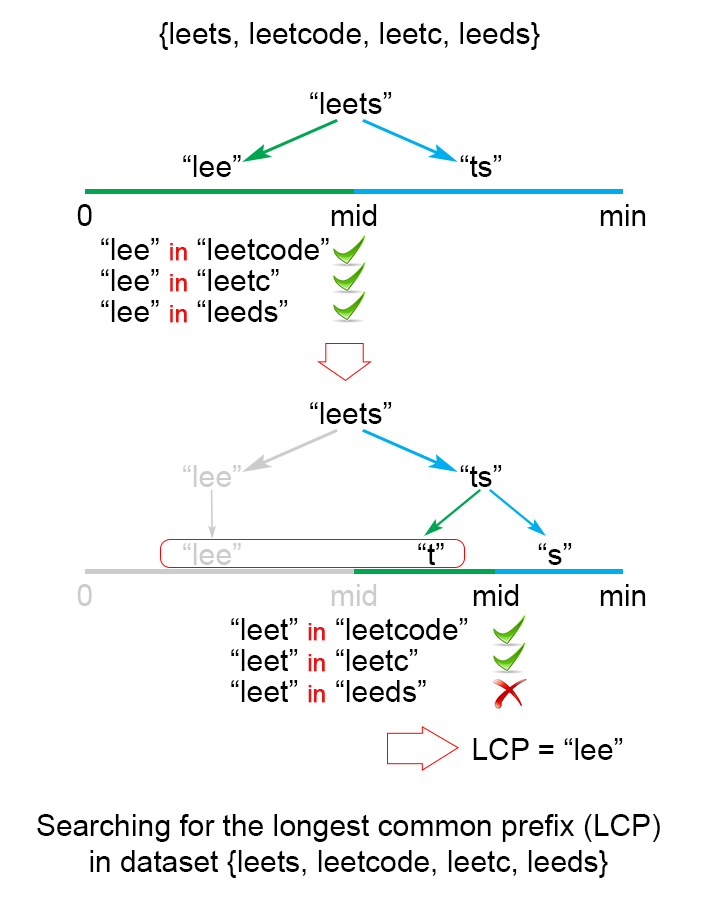
public String longestCommonPrefix(String[] strs) { if (strs == null || strs.length == 0) return ""; int minLen = Integer.MAX_VALUE; for (String str : strs) minLen = Math.min(minLen, str.length()); int low = 1; int high = minLen; while (low <= high) { int middle = (low + high) / 2; if (isCommonPrefix(strs, middle)) low = middle + 1; else high = middle - 1; } return strs[0].substring(0, (low + high) / 2); } private boolean isCommonPrefix(String[] strs, int len){ String str1 = strs[0].substring(0,len); for (int i = 1; i < strs.length; i++) if (!strs[i].startsWith(str1)) return false; return true; }
前缀树:
让我们看一个有些不同的问题:
给定一些键值字符串[S1,S2…Sn],我们要找到字符串 q 与 S 的最长公共前缀。 这样的查询操作可能会非常频繁。
我们可以通过将所有的键值 S 存储到一颗字典树中来优化最长公共前缀查询操作。 如果你想学习更多关于字典树的内容,可以从 208. 实现 Trie (前缀树) 开始。在字典树中,从根向下的每一个节点都代表一些键值的公共前缀。 但是我们需要找到字符串q 和所有键值字符串的最长公共前缀。 这意味着我们需要从根找到一条最深的路径,满足以下条件:
- 这是所查询的字符串 q 的一个前缀
- 路径上的每一个节点都有且仅有一个孩子。 否则,找到的路径就不是所有字符串的公共前缀
- 路径不包含被标记成某一个键值字符串结尾的节点。 因为最长公共前缀不可能比某个字符串本身长
算法:最后的问题就是如何找到字典树中满足上述所有要求的最深节点。 最有效的方法就是建立一颗包含字符串[S1…Sn].
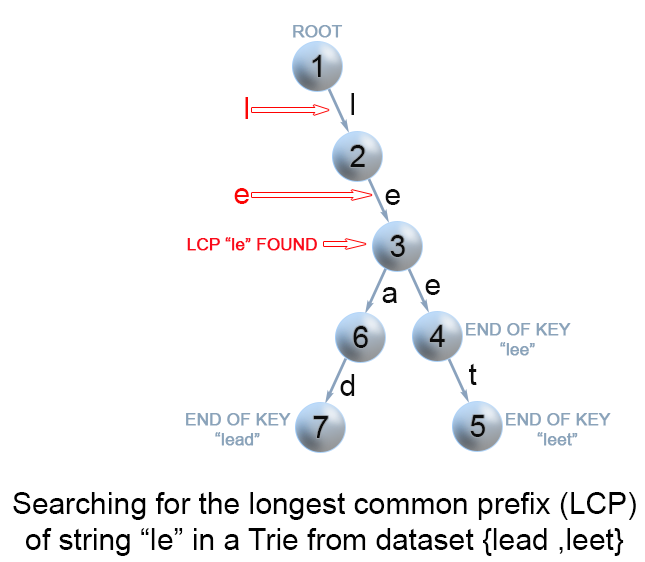
public String longestCommonPrefix(String q, String[] strs) { if (strs == null || strs.length == 0) return ""; if (strs.length == 1) return strs[0]; Trie trie = new Trie(); for (int i = 1; i < strs.length ; i++) { trie.insert(strs[i]); } return trie.searchLongestPrefix(q); } class TrieNode { // 子节点的链接数组 private TrieNode[] links; private final int R = 26; private boolean isEnd; // 非空子节点的数量 private int size; public void put(char ch, TrieNode node) { links[ch -'a'] = node; size++; } public int getLinks() { return size; } // 假设方法 containsKey、isEnd、get、put 都已经实现了 // 可以参考文章:https://leetcode.com/articles/implement-trie-prefix-tree/ } public class Trie { private TrieNode root; public Trie() { root = new TrieNode(); } // 假设方法 insert、search、searchPrefix 都已经实现了 // 可以参考文章:https://leetcode.com/articles/implement-trie-prefix-tree/ private String searchLongestPrefix(String word) { TrieNode node = root; StringBuilder prefix = new StringBuilder(); for (int i = 0; i < word.length(); i++) { char curLetter = word.charAt(i); if (node.containsKey(curLetter) && (node.getLinks() == 1) && (!node.isEnd())) { prefix.append(curLetter); node = node.get(curLetter); } else return prefix.toString(); } return prefix.toString(); } }
16.三数之和
给定一个包含 n 个整数的数组 nums,判断 nums 中是否存在三个元素 a,b,c ,使得 a + b + c = 0 ?找出所有满足条件且不重复的三元组。
注意:答案中不可以包含重复的三元组。
暴力法,超出了时间限制
class Solution { public List<List<Integer>> threeSum(int[] nums) { Arrays.sort(nums); Set<List<Integer>> result = new HashSet<>(); if(nums == null && nums.length < 3) return Collections.emptyList(); int len = nums.length; for(int i = 0; i < len - 2; i++){ for(int j = i + 1; j < len - 1; j++){ for(int k = j + 1; k < len; k++){ if(nums[i] + nums[j] + nums[k] == 0){ List<Integer> temp = new ArrayList(Arrays.asList(nums[i], nums[j], nums[k])); result.add(temp); } } } } return new ArrayList<List<Integer>>(result); } }
17.电话号码的字母组合
给定一个仅包含数字 2-9 的字符串,返回所有它能表示的字母组合。
给出数字到字母的映射如下(与电话按键相同)。注意 1 不对应任何字母。
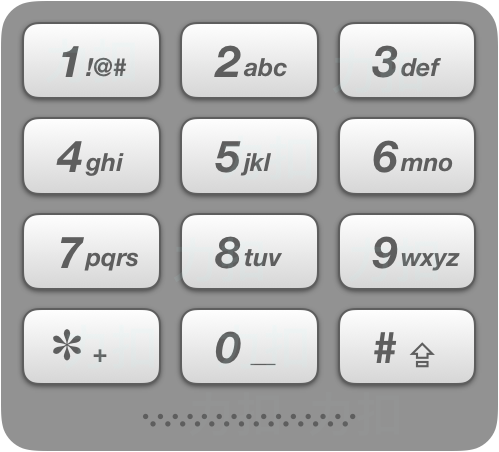
递归法,
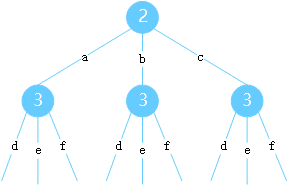
class Solution { /**private Map<String, String> phone = new HashMap<>(){{ put("2", "abc"); put("3", "def"); put("4", "ghi"); put("5", "jkl"); put("6", "mno"); put("7", "pqrs"); put("8", "tuv"); put("9", "wxyz"); }};**/ private String[] phone = new String[]{ "",//0 "",//1 "abc",//2 "def",//3 "ghi",//4 "jkl",//5 "mno",//6 "pqrs",//7 "tuv",//8 "wxyz"//9 }; private List<String> result = new ArrayList<>(); private void combinations(String s, String nextLetters){ if(nextLetters.length() == 0){ result.add(s); return; } //String index = nextLetters.substring(0, 1); String letters = phone[nextLetters.charAt(0) - '0'];//phone.get(index); for(int i = 0; i < letters.length(); i++){ String combination = letters.substring(i, i + 1); combinations(s + combination, nextLetters.substring(1)); } } public List<String> letterCombinations(String digits) { if(digits == null || digits.length() == 0) return result; combinations("", digits); return result; } }
18.删除链表的倒数第N个节点
给定一个链表,删除链表的倒数第 n 个节点,并且返回链表的头结点。
示例:
给定一个链表: 1->2->3->4->5, 和 n = 2.
当删除了倒数第二个节点后,链表变为 1->2->3->5.
说明:给定的 n 保证是有效的。
两次遍历链表,第一次得到链表的长度L,第二次删除第L-n+1个节点。
class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummpyNode = new ListNode(0); dummpyNode.next = head; ListNode cur = dummpyNode; int count = 0; while(cur != null){ count++; cur = cur.next; } if(count <= n) return null; cur = dummpyNode; for(int i = 0; ; i++){ if(i == count - n - 1){ cur.next = cur.next.next; break; } cur = cur.next; } return dummpyNode.next; } }
一次遍历,设置两个指针,它们在相距n+1,这样,当后面的指针到最后的时候,前面的指针刚好指的是倒数n-1。
class Solution { public ListNode removeNthFromEnd(ListNode head, int n) { ListNode dummpyNode = new ListNode(0); dummpyNode.next = head; ListNode pre = dummpyNode,cur = dummpyNode; for(int i = 0; cur != null;i++){ if(i > n) pre = pre.next; cur = cur.next; } pre.next = pre.next.next; return dummpyNode.next; } }
19.有效的括号
给定一个只包括 '(',')','{','}','[',']' 的字符串,判断字符串是否有效。
有效字符串需满足:
左括号必须用相同类型的右括号闭合。
左括号必须以正确的顺序闭合。
注意空字符串可被认为是有效字符串。
使用栈
class Solution { private Map<Character, Character> brackt = new HashMap<>(){{ put(')', '('); put(']', '['); put('}', '{'); }}; public boolean isValid(String s) { if(s == null) return false; Stack<Character> result = new Stack<Character>(); for(int i = 0; i < s.length(); i++){ char temp = s.charAt(i); if(brackt.containsKey(temp)){ char p = result.isEmpty()?'#':result.pop(); if(p != brackt.get(temp)) return false; }else{ result.push(temp); } } return result.isEmpty(); } }
20.合并两个有序链表
将两个有序链表合并为一个新的有序链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。
示例:
输入:1->2->4, 1->3->4
输出:1->1->2->3->4->4
暴力法依次读取两个链表的数据并比较
递归法:
我们可以如下递归地定义在两个链表里的 merge 操作(忽略边界情况,比如空链表等):
list1[0]+merge(list1[1:],list2) list1[0]<list2[0]
list2[0]+merge(list1,list2[1:]) otherwise
也就是说,两个链表头部较小的一个与剩下元素的 merge 操作结果合并。
算法:我们直接将以上递归过程建模,首先考虑边界情况。
特殊的,如果 l1 或者 l2 一开始就是 null ,那么没有任何操作需要合并,所以我们只需要返回非空链表。否则,我们要判断 l1 和 l2 哪一个的头元素更小,然后递归地决定下一个添加到结果里的值。如果两个链表都是空的,那么过程终止,所以递归过程最终一定会终止。
class Solution { public ListNode mergeTwoLists(ListNode l1, ListNode l2) { if(l1 == null){ return l2; }else if(l2 == null){ return l1; }else if(l1.val < l2.val){ l1.next = mergeTwoLists(l1.next, l2); return l1; }else{ l2.next = mergeTwoLists(l1, l2.next); return l2; } } }
官方迭代法:
class Solution { public ListNode mergeTwoLists(ListNode l1, ListNode l2) { // maintain an unchanging reference to node ahead of the return node. ListNode prehead = new ListNode(-1); ListNode prev = prehead; while (l1 != null && l2 != null) { if (l1.val <= l2.val) { prev.next = l1; l1 = l1.next; } else { prev.next = l2; l2 = l2.next; } prev = prev.next; } // exactly one of l1 and l2 can be non-null at this point, so connect // the non-null list to the end of the merged list. prev.next = l1 == null ? l2 : l1; return prehead.next; } }
21.删除排序数组中的重复项
给定一个排序数组,你需要在 原地 删除重复出现的元素,使得每个元素只出现一次,返回移除后数组的新长度。
不要使用额外的数组空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
### 解题思路 定义一个指针pre记录不重复数据所在的位置,当pre处数据与后续数据i处不同时,直接将i处数据赋值到pre+1处。 ### 代码 ```java class Solution { public int removeDuplicates(int[] nums) { int pre = 0; for(int i = 1; i < nums.length; i++){ if(nums[pre] != nums[i]){ pre++; nums[pre] = nums[i]; } } return pre + 1; } }
22.就地移除数组
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
双指针法 class Solution { public int removeElement(int[] nums, int val) { int count = 0; int pre = 0; for(int i = 0; i < nums.length; i++){ if(nums[i] != val){ nums[pre++] = nums[i]; } } return pre; } }
23.实现strStr()
实现 strStr() 函数。
给定一个 haystack 字符串和一个 needle 字符串,在 haystack 字符串中找出 needle 字符串出现的第一个位置 (从0开始)。如果不存在,则返回 -1。
示例 1:
输入: haystack = "hello", needle = "ll"
输出: 2
示例 2:
输入: haystack = "aaaaa", needle = "bba"
输出: -1
说明:
当 needle 是空字符串时,我们应当返回什么值呢?这是一个在面试中很好的问题。
对于本题而言,当 needle 是空字符串时我们应当返回 0 。这与C语言的 strstr() 以及 Java的 indexOf() 定义相符。
暴力法
class Solution { public int strStr(String haystack, String needle) { if(haystack.length() < needle.length()) return -1; if(needle.equals("")) return 0; int temp = 0; for(int i = 0, j = 0; i < haystack.length(); i++){ temp = i; while(haystack.charAt(i) == needle.charAt(j)) { i++; j++; if(i == haystack.length() && j != needle.length()) return -1; if(j == needle.length()) return i - j; } i = temp; j = 0; } return -1; } }
字串逐一比较法:
class Solution { public int strStr(String haystack, String needle) { int L = needle.length(), n = haystack.length(); for (int start = 0; start < n - L + 1; ++start) { if (haystack.substring(start, start + L).equals(needle)) { return start; } } return -1; } }
双指针法,当出现不同的字符时,马上回溯
class Solution { public int strStr(String haystack, String needle) { int L = needle.length(), n = haystack.length(); if (L == 0) return 0; int pn = 0; while (pn < n - L + 1) { // find the position of the first needle character // in the haystack string while (pn < n - L + 1 && haystack.charAt(pn) != needle.charAt(0)) ++pn; // compute the max match string int currLen = 0, pL = 0; while (pL < L && pn < n && haystack.charAt(pn) == needle.charAt(pL)) { ++pn; ++pL; ++currLen; } // if the whole needle string is found, // return its start position if (currLen == L) return pn - L; // otherwise, backtrack pn = pn - currLen + 1; } return -1; } }
24.两数相除
给定两个整数,被除数 dividend 和除数 divisor。将两数相除,要求不使用乘法、除法和 mod 运算符。
返回被除数 dividend 除以除数 divisor 得到的商。
示例 1:
输入: dividend = 10, divisor = 3
输出: 3
示例 2:
输入: dividend = 7, divisor = -3
输出: -2
说明:
被除数和除数均为 32 位有符号整数。
除数不为 0。
假设我们的环境只能存储 32 位有符号整数,其数值范围是 [−231, 231 − 1]。本题中,如果除法结果溢出,则返回 231 − 1。
解题思路:
计算a/b(如果是负数,先转成正数,保证a和b都不是负数),基本思路是a一直减b,每减一次result+=1,直到0<= a <b(这里的a指的是上一次减完之后剩余的a)。
例如7/3,7 - 3 - 3 = 1, 0 <= 1 < 3,结果为2。
如果每次只减b,耗时太长,因此借助移位操作,每次减 b*2^n,同时result+=2^n。这里要满足b*2^n <= a(这里的a指的是上一次减完之后剩余的a)。
例如100/3,100 - 3*32 - 3 = 1,result = 32+1 = 33。
对于溢出的问题,考虑几种情况:
a = -2^31, b = -1, a/b = 2^31,直接返回 2^32-1
a = -2^31, b = -2^31, a/b = 1,直接返回1
a != -2^31, b = -2^31, a/b = 0,直接返回0
a = -2^31, b != -2^31,因为需要将a、b转成正数,而a转换后会溢出,因此先在a的基础上加 / 减b,使其绝对值减小,同时最终的result也需要再加上-1或1(也就是代码中的fix)。
class Solution { public int divide(int a, int b) { // a = -2^31, b = -1, a/b = 2^31 if (a == Integer.MIN_VALUE && b == -1) return Integer.MAX_VALUE; // a = -2^31, b = -2^31, a/b = 1 if (a == Integer.MIN_VALUE && b == Integer.MIN_VALUE) return 1; // a != -2^31, b = -2^31, a/b = 0 if (b == Integer.MIN_VALUE) return 0; // a = -2^31, b != -2^31: a <= a + abs(b), fix = b > 0 ? -1 : 1 int fix = 0; if (a == Integer.MIN_VALUE) { if (b > 0) { a += b; fix = -1; } else { a -= b; fix = 1; } } boolean neg = false; if (a < 0) { a = -a; neg = !neg; } if (b < 0) { b = -b; neg = !neg; } int result = 0; while (a >= b) { int x = b; int r = 1; while (x <= (a>>1)) { x <<= 1; r <<= 1; } a -= x; result += r; } return (neg ? -result : result) + fix; } }
25.Pow(x, n)
实现 pow(x, n) ,即计算 x 的 n 次幂函数。
示例 1:
输入: 2.00000, 10
输出: 1024.00000
示例 2:
输入: 2.10000, 3
输出: 9.26100
示例 3:
输入: 2.00000, -2 输出: 0.25000 解释: 2-2 = 1/22 = 1/4 = 0.25
说明:
-100.0 < x < 100.0
n 是 32 位有符号整数,其数值范围是 [−231, 231 − 1] 。
暴力法:超出时间限制
class Solution { public double myPow(double x, int n) { if(x == 1 && n == 1) return x; if(n < 0){ n = -n; x = 1/x; } double result = 1.0; for(int i = 0; i < n; i++){ result *= x; } return result; } }
方法2:快速幂算法(递归)
直观想法:假定我们已经得到了 x ^ n的结果,我们如何得到 x ^ {2 * n}的结果?很明显,我们不需要将 x 再乘 n 次。使用公式 (x ^ n) ^ 2 = x ^ {2 * n},我们可以在一次计算内得到 x ^ {2 * n}的值。使用该优化方法,我们可以降低算法的时间复杂度。
算法:假定我们已经得到了 x ^ {n / 2}的结果,并且我们现在想得到 x ^ n的结果。我们令 A 是 x ^ {n / 2}的结果,我们可以根据 n 的奇偶性来分别讨论 x ^ n的值。如果 n 为偶数,我们可以用公式 (x ^ n) ^ 2 = x ^ {2 * n}来得到 x ^ n = A * A。如果 n 为奇数,那么 A * A = x ^ {n - 1}。直观上看,我们需要再乘一次 x ,即 x ^ n = A * A * x。
该方法可以很方便的使用递归实现。我们称这种方法为 "快速幂",因为我们只需最多O(logn) 次运算来得到 x ^ n。
class Solution { private double fastPow(double x, long n) { if (n == 0) { return 1.0; } double half = fastPow(x, n / 2); if (n % 2 == 0) { return half * half; } else { return half * half * x; } } public double myPow(double x, int n) { long N = n; if (N < 0) { x = 1 / x; N = -N; } return fastPow(x, N); } }
方法 3:快速幂算法(循环)
直观想法:
使用公式 x ^ {a + b} = x ^ a * x ^ b,我们可以将 n 看做一系列正整数之和,n = ∑bi。如果我们可以很快得到 x ^ {b_i}的结果,计算 x ^ n的总时间将被降低。
算法:
我们可以使用 n 的二进制表示来更好的理解该问题。使 n 的二进制从最低位 (LSB) 到最高位 (MSB) 表示为b_1, b_2, ..., b_{length\_limit}。对于第 i 位为,如果 b_i = 1,意味着我们需要将结果累乘上 x ^ {2 ^ i}。
这似乎不能有效率上的提升,因为 \sum_i b_i * 2 ^ i = n∑bi∗2i=n 。但是使用上面提到的公式 (x ^ n) ^ 2 = x ^ {2 * n},我们可以进行改进。初始化 x ^ 1 = x,对于每一个 $ i > 1$ ,我们可以在一步操作中使用 x ^ {2 ^ {i - 1}}来得到 x ^ {2 ^ i}。由于 b_i的个数最多为O(logn) ,我们可以在 O(logn) 的时间内得到所有的 x ^ {2 ^ i}。在那之后,对于所有满足 b_i = 1的 i,我们可以用结果累乘 x ^ {2 ^ i}。这也只需要O(logn) 的时间。
class Solution { public double myPow(double x, int n) { long N = n; if (N < 0) { x = 1 / x; N = -N; } double ans = 1; double current_product = x; for (long i = N; i > 0; i /= 2) { if ((i % 2) == 1) { ans = ans * current_product; } current_product = current_product * current_product; } return ans; } }
26.跳跃游戏
给定一个非负整数数组,你最初位于数组的第一个位置。
数组中的每个元素代表你在该位置可以跳跃的最大长度。
你的目标是使用最少的跳跃次数到达数组的最后一个位置。
示例:
输入: [2,3,1,1,4]
输出: 2
解释: 跳到最后一个位置的最小跳跃数是 2。
从下标为 0 跳到下标为 1 的位置,跳 1 步,然后跳 3 步到达数组的最后一个位置。
说明:
假设你总是可以到达数组的最后一个位置。
顺瓜摸藤,我们知道最终要到达最后一个位置,然后我们找前一个位置,遍历数组,找到能到达它的位置,离它最远的就是要找的位置。
然后继续找上上个位置,最后到了第 0 个位置就结束了。至于离它最远的位置,其实我们从左到右遍历数组,第一个满足的位置就是我们要找的。
class Solution { public int jump(int[] nums) { int position = nums.length - 1; int result = 0; while(position > 0){ for(int i = 0; i < position; i++){ if(nums[i] >= position - i){ position = i; result++; break; } } } return result; } }
顺藤摸瓜,贪婪算法,我们每次在可跳范围内选择可以使得跳的更远的位置
class Solution { public int jump(int[] nums) { int maxPosition = 0; int end = 0, steps = 0; for(int i = 0; i < nums.length - 1; i++){ maxPosition = Math.max(maxPosition, nums[i] + i); if(i == end) { end = maxPosition; steps++; } } return steps; } }
27.k个一组翻转链表
给你一个链表,每 k 个节点一组进行翻转,请你返回翻转后的链表。
k 是一个正整数,它的值小于或等于链表的长度。
如果节点总数不是 k 的整数倍,那么请将最后剩余的节点保持原有顺序。
示例:
给你这个链表:1->2->3->4->5 当 k = 2 时,应当返回: 2->1->4->3->5 当 k = 3 时,应当返回: 3->2->1->4->5
说明:
你的算法只能使用常数的额外空间。
你不能只是单纯的改变节点内部的值,而是需要实际进行节点交换。
每k个节点为一组,调换顺序。时间复杂度:N,空间复杂度为常数
class Solution { public ListNode reverseKGroup(ListNode head, int k) { int len = 0; ListNode dummyNode = new ListNode(0); ListNode cur = head; dummyNode.next = head; ListNode tail = dummyNode, index = dummyNode; while(cur != null){ len++; cur = cur.next; } cur = dummyNode.next; for(int i = 0; i < len/k; i++){ tail = cur; cur = cur.next; for(int j = 1; j < k; j++){ ListNode next = cur.next; tail.next = next; cur.next = index.next; index.next = cur; cur = next; } index = tail; } if(cur != null){ index.next = cur; } return dummyNode.next; } }
尾插法class Solution { public ListNode reverseKGroup(ListNode head, int k) { ListNode dummy = new ListNode(0); dummy.next = head; ListNode pre = dummy; ListNode tail = dummy; while (true) { int count = 0; while (tail != null && count != k) { count++; tail = tail.next; } if (tail == null) break; ListNode head1 = pre.next; while (pre.next != tail) { ListNode cur = pre.next; pre.next = cur.next; cur.next = tail.next; tail.next = cur; } pre = head1; tail = head1; } return dummy.next; } }
递归法 class Solution { public ListNode reverseKGroup(ListNode head, int k) { ListNode cur = head; int count = 0; while (cur != null && count != k) { cur = cur.next; count++; } if (count == k) { cur = reverseKGroup(cur, k); while (count != 0) { count--; ListNode tmp = head.next; head.next = cur; cur = head; head = tmp; } head = cur; } return head; } }
28.下一个排列
实现获取下一个排列的函数,算法需要将给定数字序列重新排列成字典序中下一个更大的排列。
如果不存在下一个更大的排列,则将数字重新排列成最小的排列(即升序排列)。
必须原地修改,只允许使用额外常数空间。
以下是一些例子,输入位于左侧列,其相应输出位于右侧列。
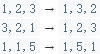
一次遍历法
class Solution { private void swap(int[] nums, int i, int j){ int temp = nums[i]; nums[i] = nums[j]; nums[j] = temp; } private void reverse(int[] nums, int start){ for(int i = start, j = nums.length - 1; i < j; i++, j--){ swap(nums, i, j); } } public void nextPermutation(int[] nums) { if(nums.length == 1) return; int i = nums.length - 2; while(i >= 0 && nums[i] >= nums[i + 1]) i--; if(i >= 0){ int j = nums.length - 1; while(j > 0 && nums[j] <= nums[i]) j--; swap(nums, i, j); } reverse(nums, i + 1); } }
29.N皇后
回溯法
class Solution { private List<List<String>> result = new ArrayList<>(); private int[] array; public List<List<String>> solveNQueens(int n) { array = new int[n]; check(0, n); return result; } private void check(int level, int n){ if (level == n){ parseList(n); return; } for(int i = 0; i < n; i++){ array[level] = i; if(judge(level)){ check(level + 1, n); } } } private boolean judge(int level){ for(int i = 0; i < level; i++){ if(array[i] == array[level] || Math.abs(level - i) == Math.abs(array[level] - array[i])){ return false; } } return true; } private void parseList(int n){ List<String> temp = new ArrayList<String>(); for(int i = 0; i < array.length; i++){ StringBuilder sb = new StringBuilder(); for(int j = 0; j < n; j++){ if(j == array[i]){ sb.append("Q"); }else{ sb.append("."); } } temp.add(sb.toString()); } result.add(temp); } }
30.正则表达式匹配
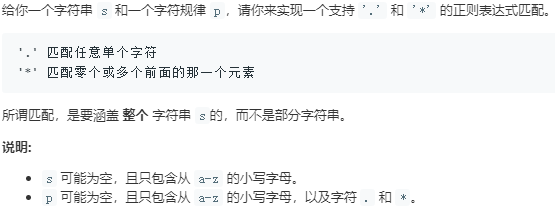
回溯法
class Solution { public boolean isMatch(String s, String p) { if(p.isEmpty()) return s.isEmpty(); boolean firstMatch = ((!s.isEmpty()) && (s.charAt(0) == p.charAt(0) || p.charAt(0) == '.')); if((p.length() >= 2) && (p.charAt(1) == '*')){ return (isMatch(s, p.substring(2)) || (firstMatch) && isMatch(s.substring(1), p)); }else{ return (firstMatch && isMatch(s.substring(1), p.substring(1))); } } }
31.通配符匹配




