KMP字符串匹配算法学习
- KMP算法简介
引出原由：由于传统字符串配算法的效率低下，对于大量的重复字符的字符串要重复挨个遍历。
发明者：D.E.Knuth、J.H.Morris和V.R.Pratt。 - 传统字符串匹配算法
/** * @brief genMatch * @param s 主字符串 * @param p 匹配字符串 * @return 匹配的位置，成功返回匹配到的下标，失败返回-1 */ int genMatch(const char *s, const char *p) { int sLen = strlen(s); int pLen = strlen(p); int i = 0; int j = 0; if (sLen < 0 || pLen < 0 || sLen < pLen) return -1; while (i < sLen && j < pLen) { if (s[i] == p[j]) { i ++; j ++; } else { i = i - j + 1; // i回溯(i - (j - 1)) j = 0; // j 从新回到匹配串的开头 } } return j == pLen ? i - j : -1; }
- 传统字符串匹配算法性能问题讨论
用匹配字符串p去匹配主字符串s，在i=6,j=4时发生失配：i 0 1 2 3 4 5 6 7 8 9 10 11 s
A B A B C A D C A C B A p A B C A C j 0 1 2 3 4 当s串(i=6), p串(j=4)匹配失效，此时，按照传统算法，应当将p的第 1 个字符 A(j=0) 滑动到与s中第4个字符 B(i=3) 对齐再进行匹配：
在匹配的过程中，主串s的i发生了“回溯”（从6变成了3），然而这样的回溯本身不是需要的，在我们上次匹配的时候我们就已经知道了p[m]=s[n], 其中(m, n)∈{n-m=2, 0<=m<=3, 2<=n<=5}，而且p[0]不与其后3元素相等，那么p[0]就肯定不与s[3], s[4], s[5]相等，此3步的比较就是不需要的。i 0 1 2 3 4 5 6 7 8 9 10 11 s
A B A B C A D C A C B A p A B C A C j 0 1 2 3 4
我们希望直接让j=0与i=5对齐，然后直接比较p[j+1]的与s[i]的值（此时j=0, i=5）。
在这个测试用例中，相对于第一个表格，我们直接将p向右滑动3个字符，使s中 i=5 的字符与t中 j=0 的字符对齐，再匹配s中 i=6 的字符与p中 j=1 的字符。
i 0 1 2 3 4 5 6 7 8 9 10 11 s
A B A B C A D C A C B A p A B C A C j 0 1 2 3 4 - KMP算法的原理
对于任意的s和p，当s中下标为i的字符串和p中下标为j的字符串失配时，我们假定当使p滑动，让其下标为k的字符与s中下标为i的字符“对齐”继续比较（j=next[j],i不变），那么，如何得到该k，也就是我们说的next数组？
我们知道，所谓对齐就是要满足以下条件：
....(1)
另一方面，在失配时我们已经得到过一部分匹配结果：
....(2)
由(1)、(2)得到：
....(3)
详细推论过程如下图所示：
- next数组获得方式
a.人工推算方式
next数组的表达式如下：
我们只需要去目测数组下标0->(j-1)的最长匹配的前缀和后缀字符数即可。例如：
给定字符串“ABCDABD”，可求得它的next 数组如下：
分析：j 0 1 2 3 4 5 6 p[j] A B C D A B D next[j] -1 0 0 0 0 1 2
1.根据next数组的表达式，当j=0时，next[j=0]=-1毋庸置疑；
2.当j=1时，p0...pj-1=p0，只有一个元素A，不存在前缀，后缀的说法，所以属于其他情况，next[j=1]=0；
3.当j=2时，p0...pj-1=p0p1，只有两个元素AB，明显A!=B，不存在前后缀相等的情况，next[j=2]=0；
4.当j=3时，p0...pj-1=p0p1p2，为ABC，依然不存在前后缀相等的情况（AB!=BC,A!=C），next[j=3]=0;
...
6.当j=5时，p0...pj-1=p0p1p2p3p4，为ABCDA，存在前后缀相等的情况（A==A，第一个A和最后一个A，匹配的最大字符数为1），next[j=5]=1;
7.当j=6时，p0...pj-1=p0p1p2p3p4p5，为ABCDAB，存在前后缀相等的情况（AB==AB，匹配的最大字符数为2），next[j=6]=2。
b.代码递推
next数组的初始条件是next[0] = -1，设next[j] = k，则有：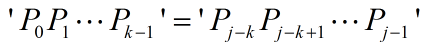
那么，next[j+1]有两种情况：
①
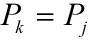，则有：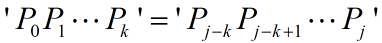
此时next[j+1] = next[j] + 1 = k + 1
(人工推算方式 表格中j=6就是在j=5的next之上+1，明显前面都匹配了(A)，一旦该值((j+1)5)(B)匹配了前面那个已经被((j)4)(A)匹配的值(下标为0)(A)的后面那个值(下标为1)(B)，自然就是+1)②
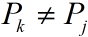， 其实就是一个去判断p[next[k]]?=p[j], p[next[next[k]]]?=p[j]...的一个递归过程，如图所示：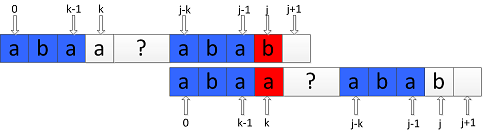
此时需要将P向右滑动之后继续比较P中index为 j 的字符与index为 next[k] 的字符：
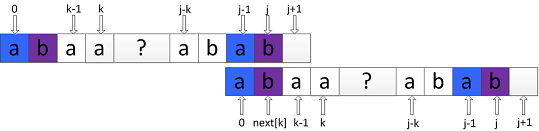
值得注意的是，上面的“向右滑动”本身就是一个kmp在失配情况下的滑动过程，将这个过程看 P 的自我匹配，则有：
如果
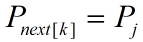，则next[j+1] = next[k] + 1；否则，继续将 P 向右滑动，直至匹配成功，或者不存在这样的匹配，此时next[j+1] = 0。
下面贴一个July的一个案例分析（个人觉得很不错）：
如下图所示，假定给定模式串ABCDABCE，且已知next [j] = k（相当于“p0 pk-1” = “pj-k pj-1” = AB，可以看出k为2），现要求next [j + 1]等于多少？因为pk = pj = C，所以next[j + 1] = next[j] + 1 = k + 1（可以看出next[j + 1] = 3）。代表字符E前的模式串中，有长度k+1 的相同前缀后缀。但如果pk != pj 呢？说明“p0 pk-1 pk” ≠ “pj-k pj-1 pj”。换言之，当pk != pj后，字符E前有多大长度的相同前缀后缀呢？很明显，因为C不同于D，所以ABC 跟 ABD不相同，即字符E前的模式串没有长度为k+1的相同前缀后缀，也就不能再简单的令：next[j + 1] = next[j] + 1 。所以，咱们只能去寻找长度更短一点的相同前缀后缀。结合上图来讲，若能在前缀“ p0 pk-1 pk ” 中不断的递归前缀索引k = next [k]，找到一个字符pk’ 也为D，代表pk’ = pj，且满足p0 pk'-1 pk' = pj-k' pj-1 pj，则最大相同的前缀后缀长度为k' + 1，从而next [j + 1] = k’ + 1 = next [k' ] + 1。否则前缀中没有D，则代表没有相同的前缀后缀，next [j + 1] = 0。那为何递归前缀索引k = next[k]，就能找到长度更小的相同前缀后缀呢？这又归根到next数组的含义。为了寻找长度相同的前缀后缀，我们拿前缀 p0 pk-1 pk 去跟后缀pj-k pj-1 pj匹配，如果pk 跟pj 失配，下一步就是用p[next[k]] 去跟pj 继续匹配，如果p[ next[k] ]跟pj还是不匹配，则下一步用p[ next[ next[k] ] ]去跟pj匹配。相当于模式串的自我匹配，所以不断的递归k = next[k]，直到要么找到长度更小的相同前缀后缀，要么没有长度更小的相同前缀后缀。 - 初次实现KMP算法
通过前面对KMP算法的分析，知道KMP算法的核心就是两步：1.计算next数组；2.在传统的匹配算法上，i不去回溯且j=next[j]。
/** * @brief getNext 优化前的获取next数组的函数 * @param p 匹配字符串 * @param next 用来存放失配后，j的值的数组 */ void getNext(const char *p, int *next) { int j = 0; int k = -1; int pLen = strlen(p); if (next == NULL || pLen < 1) return ; next[0] = -1; while (j < pLen - 1) { if (k == -1 || p[k] == p[j]) { k ++; j ++; next[j] = k; } else { k = next[k]; } } }
/** * @brief KMP_Match * @param s 主字符串 * @param p 匹配字符串 * @return */ int KMP_Match(const char *s, const char *p) { int sLen = strlen(s); int pLen = strlen(p); int i = 0; int j = 0; int *next = new int[pLen + 1]; if (sLen < 1 || pLen < 1 || sLen < pLen) { delete []next; return -1; } getNext(p, next); while (i < sLen && j < pLen) { if (j == -1 || p[j] == s[i]) { i ++; j ++; } else { j = next[j]; } } delete []next; return j == pLen ? i - j : -1; }
- 获取next函数的优化
注意到，上面的getNext函数还存在可以优化的地方，比如：i 0 1 2 3 4 5 6 7 8 s
A A A B A A A A B p A A A A B j 0 1 2 3 4 此时，i=3、j=3时发生失配，next[3]=2，此时还需要进行 3 次比较：
i=3, j=2;
i=3, j=1;
i=3, j=0。
而实际上，因为i=3, j=3时就已经知道a!=b，而之后的三次依旧是拿 a 和 b 比较，因此这三次比较都是多余的。
此时应当直接将P向右滑动4个字符，进行 i=4， j=0的比较。
一般而言，在getNext函数中，next[i]=j，也就是说当p[i]与S中某个字符匹配失败的时候，用p[j]继续与S中的这个字符比较。
如果p[i]==p[j]，那么这次比较是多余的（如同上面的例子），此时应该直接使next[i]=next[j]。
优化后的getNext函数：/** * @brief getNext 优化后的获取next数组的函数 * @param p 匹配字符串 * @param next 用来存放失配后，j的值的数组 */ void getNext(const char *p, int *next) { int j = 0; int k = -1; int pLen = strlen(p); if (next == NULL || pLen < 1) return ; next[0] = -1; while (j < pLen - 1) { if (k == -1 || p[k] == p[j]) { k ++; j ++; next[j] = p[k] != p[j] ? k : next[k]; } else { k = next[k]; } } }
- 参考文献
《大话数据结构》-程杰-清华大学出版社-2011-6-1
KMP算法学习&总结-GoAgent-http://www.cnblogs.com/goagent/archive/2013/05/16/3068442.html
从头到尾彻底理解KMP（2014年8月22日版）-v_JULY_v-http://blog.csdn.net/v_july_v/article/details/7041827
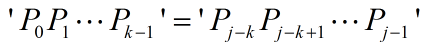
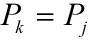，则有：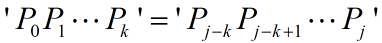
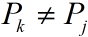， 其实就是一个去判断p[next[k]]?=p[j], p[next[next[k]]]?=p[j]...的一个递归过程，如图所示：
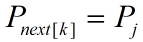，则next[j+1] = next[k] + 1；