斐波拉契数列

简介
历史上有一个有名的关于兔子的问题:假设有一对兔子,长两个月它们就算长大成年了。然后以后每个月都会生出1对兔子,生下来的兔子也都是长两个月就算成年,然后每个月也都会生出1对兔子了。这里假设兔子不会死,每次都是只生1对兔子。
第一个月,只有1对小兔子;
第二个月,小兔子还没长成年,还是只有1对兔子;
第三个月,兔子长成年了,同时生了1对小兔子,因此有两对兔子;
第四个月,成年兔子又生了1对兔子,加上自己及上月生的小兔子,共有3对兔子;
第五个月,成年兔子又生了1对兔子,第三月生的小兔子现在已经长成年了且生了1对小子,加上本身两只成年兔子及上月生的小兔子,共5对兔子;
这样过了一年之后,会有多少对兔子了呢?
我们可以把这些兔子的数量以对为单位列出数字就能得到一组数字:1、1、2、3、5、8、13、21、34、55、89、144、233。所以,过了一年之后,总共会有233对兔子了。那么续往下呢?
其实这组数字可以形成一个有规律的数列,我们把这个数列叫做“斐波那契数列”。在这个数列中的数字,就被称为“斐波那契数”。这个数列是在1228年意大利数学家斐波那契首先提出的。这个数列的规律是这样的:它的第一项、第二项是1,而从第三项起每一项都等于它的前两项之和。所以,如果不考虑兔子的死亡问题,我们还可以继续往下算出n年后兔子繁殖的数量。
代码实现
public class Fib {
// O(2^n)
public static int fib1(int n) {
if (n <= 1) return n;
return fib1(n - 1) + fib1(n - 2);
}
// O(n)
public static int fib2(int n) {
if (n <= 1) return n;
int first = 0;
int second = 1;
for (int i = 0; i < n - 1; i++) {
int sum = first + second;
first = second;
second = sum;
}
return second;
}
public static void main(String[] args) {
int result = fib2(64);
System.out.println(result);
}
}
如何评判一个算法的好坏?
一般从以下维度来评估算法的优劣
- 正确性、可读性、健壮性(对不合理输入的反应能力和处理能力)
- 时间复杂度(time complexity):估算程序指令的执行次数(执行时间)
- 空间复杂度(space complexity):估算所需占用的存储空间
大O表示法(Big O)
- 一般用大O表示法来描述复杂度,它表示的是数据规模 n 对应的复杂度
- 忽略常数、系数、低阶
9 >> O(1)
2n + 3 >> O(n)
n^2 + 2n + 6 >> O(n^2 )
4n^3 + 3n^2 + 22n + 100 >> O(n^3 )
注意:大O表示法仅仅是一种粗略的分析模型,是一种估算,能帮助我们短时间内了解一个算法的执行效率
log 2^n = log 2^9 ∗ log 9^n
所以 log 2^n 、log 9^n 统称为 logn

O(1) < O(logn) < O(n) < O(nlogn) < O(n 2 ) < O(n^3 ) < O(2*n ) < O(n!) < O(n^n )
数据规模较小时
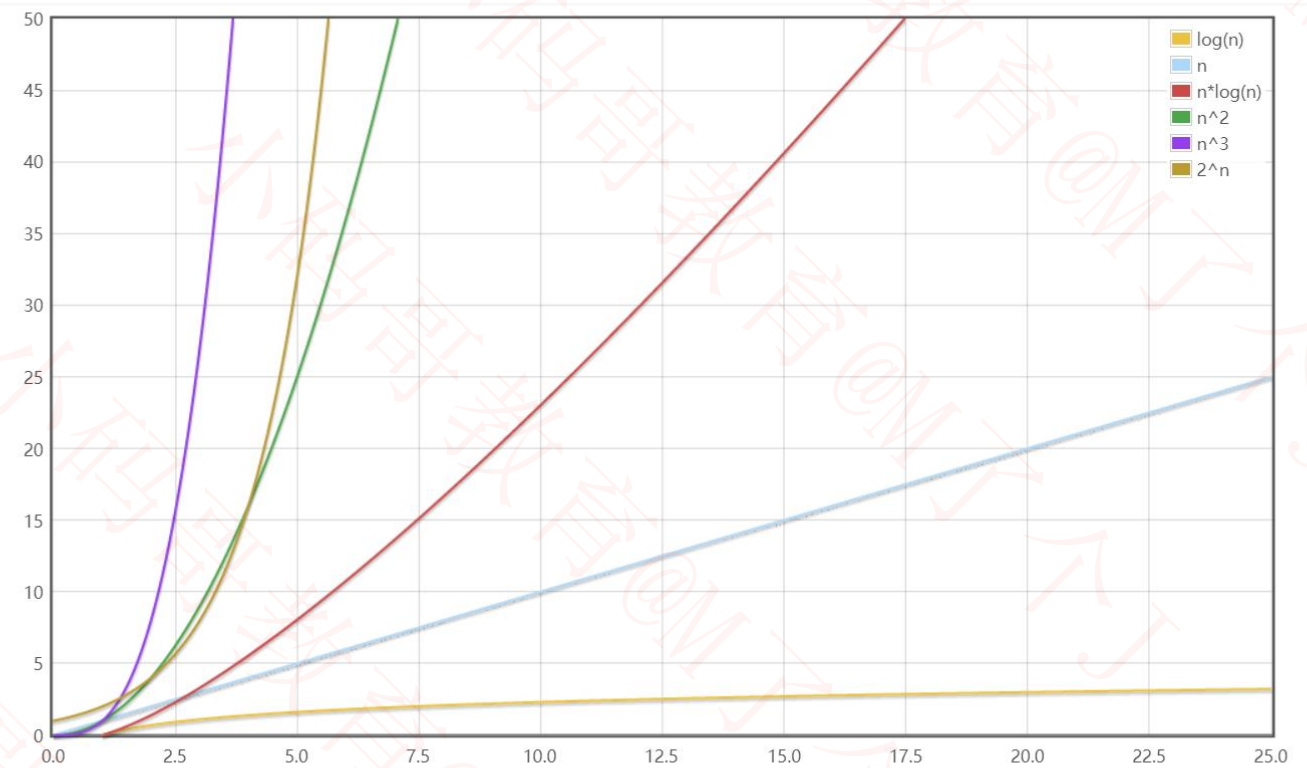
数据规模较大时
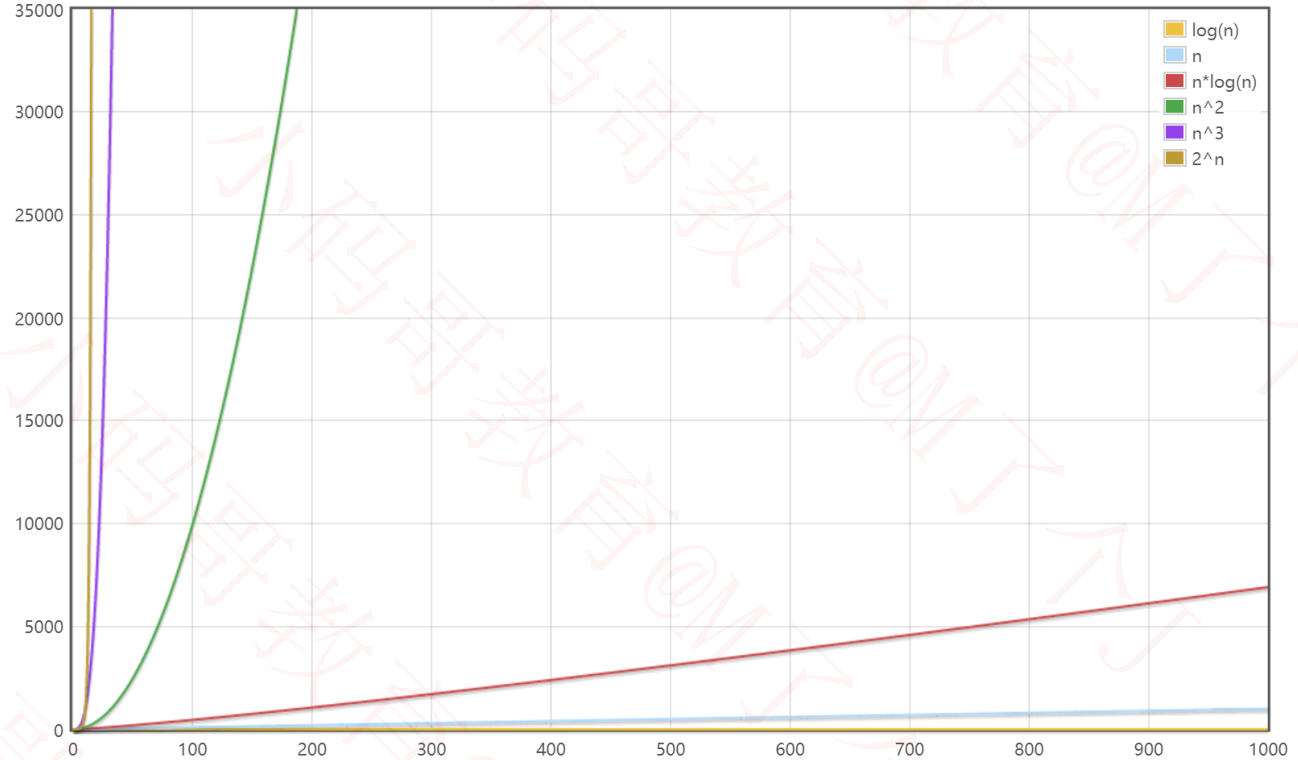
fib函数的时间复杂度分析

算法的优化方向
- 用尽量少的存储空间
- 用尽量少的执行步骤(执行时间)


