（转）本文将展示几种基本图形的生成算法,包括:圆面,圆球,圆柱,圆锥,圆环,圆管,螺旋环,圆螺,五角环,金字塔,正8面体.使用自己定义语法的脚本代码生成数学图形.相关软件参见:数学图形可视化工具,该软件免费开源.
之前一篇文章:数学图形之将曲线(curve)转化成曲面管,写完之后,意识到这种生成曲面管的脚本代码太过复杂了.本来其输入为曲线+管的半径,那么完全可以将其改成一句话的形式.我需要在生成曲线的代码后面加上一句话就可以将其转化成曲面管.pipe = radius[0.5], type[0]
实现了由"pipe"脚本解析后,我想到曲线是可以通过旋转,缩放,平移,这三种基础的图形变换,转化成曲面的.OK,于是又实现了如下的语法:
(1)绕空间中任意一条直线进行旋转, 可以生成旋转面
rotate = anchor[0, 0, 0], axis[0,1, 0], angle[0, 2*PI]
(2)沿着一个任意朝向移动顶点, 可以生成柱面
translate = dir[0, 1, 0], dis[0, 5]
(3)以空间中任意一点为基点,对曲线上的顶点进行缩放
scale = anchor[0, 0, 0], x[1, 0], z[1, 0]
最后,由曲线到曲面会增加一个维度的数据,需要设置其数据大小:surface_slices = 72
下面将展示使用这几种新加的语句生成的图形与脚本代码:
圆面
vertices = 360 u = from 0 to (2*PI) r = 5.0 x = r*sin(u) y = r*cos(u) scale = anchor[0, 0, 0], x[1, 0], y[1, 0]
圆球
常规生成球面的算法参见:数学图形之球面
vertices = 360 u = from 0 to (PI) r = 2.0 x = r*sin(u) y = r*cos(u) rotate = anchor[0, 0, 0], axis[0,1, 0], angle[0, 2*PI]
圆柱
常规生成圆柱的算法参见:数学图形之圆柱面
vertices = 360 u = from 0 to (2*PI) r = 2.0 x = r*sin(u) z = r*cos(u) translate = dir[0, 1, 0], dis[0, 5]
圆锥
常规生成圆锥的算法参见:数学图形之锥体
vertices = 360 u = from 0 to (2*PI) r = 2.0 x = r*sin(u) z = r*cos(u) translate = dir[0, 1, 0], dis[0, 5] scale = anchor[0, 0, 0], x[1, 0], z[1, 0]
圆环
常规生成圆环的算法参见:数学图形之圆环
vertices = 360 u = from 0 to (2*PI) r = 2.0 x = r*sin(u) + 5 y = r*cos(u) surface_slices = 72 rotate = anchor[0, 0, 0], axis[0,1, 0], angle[0, 2*PI]
圆管
vertices = 360 u = from 0 to (2*PI) r = 5.0 x = r*sin(u) z = r*cos(u) pipe = radius[0.5], type[0]
螺旋环
常规生成螺旋环的算法参见:数学图形之螺旋管
vertices = 100 u = from 0 to (2*PI) r = 1.0 x = r*sin(u) + 5 y = r*cos(u) surface_slices = 200 rotate = anchor[0, 0, 0], axis[0, 1, 0], angle[0, 8*PI] translate = dir[0, 1, 0], dis[0, 9]
圆螺
vertices = 100 u = from 0 to (2*PI) r = 1.0 x = r*sin(u) + 5 y = r*cos(u) surface_slices = 200 scale = anchor[0, 0, 0], x[1, 0], y[1, 0] rotate = anchor[0, 0, 0], axis[0, 1, 0], angle[0, 8*PI] translate = dir[0, 1, 0], dis[0,6]
五角环
vertices =6 u = from 0 to (2*PI) r = 2.0 x = r*sin(u) + 5 y = r*cos(u) surface_slices = 6 rotate = anchor[0, 0, 0], axis[0,1, 0], angle[0, 2*PI]
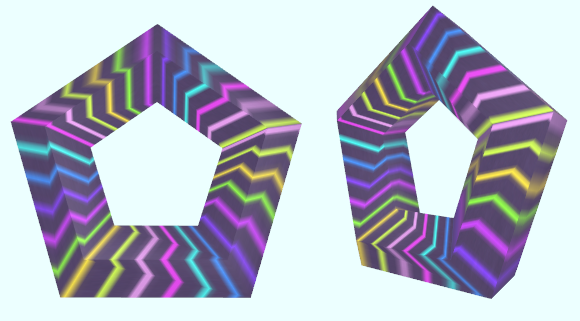
金字塔
vertices =5 u = from 0 to (2*PI) r = 2.0 x = r*sin(u) z = r*cos(u) surface_slices = 3 translate = dir[0, 1, 0], dis[0, 2] scale = anchor[0, 0, 0], x[1, 0], z[1, 0]
正8面体
vertices =3 u = from 0 to (PI) r = 2.0 x = r*sin(u) y = r*cos(u) surface_slices = 5 rotate = anchor[0, 0, 0], axis[0,1, 0], angle[0, 2*PI]
