寻路算法之A*算法详解

前言

在实际开发中我们会经常用到寻路算法，例如MMOARPG游戏魔兽中，里面的人物行走为了模仿真实人物行走的体验，会选择最近路线达到目的地，期间会避开高山或者湖水，绕过箱子或者树林，直到走到你所选定的目的地。这种人类理所当然的行为，在计算机中却需要特殊的算法去实现，常用的寻路算法主要有宽度最优搜索^[1]、Dijkstra算法、贪心算法、A*搜索算法、B*搜索算法^[2]、导航网格算法、JPS算法^[3]等，学习这些算法的过程就是不断抽象人类寻路决策的过程。本文主要以一个简单空间寻路为例，对A*算法进行分析实现。

介绍

A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法，也是解决许多搜索问题的常用启发式算法，算法中的距离估算值与实际值越接近，最终搜索速度越快。之后涌现了很多预处理算法（如ALT，CH，HL等等），在线查询效率是A*算法的数千甚至上万倍。

问题

在包含很多凸多边形障碍的空间里，解决从起始点到终点的机器人导航问题。

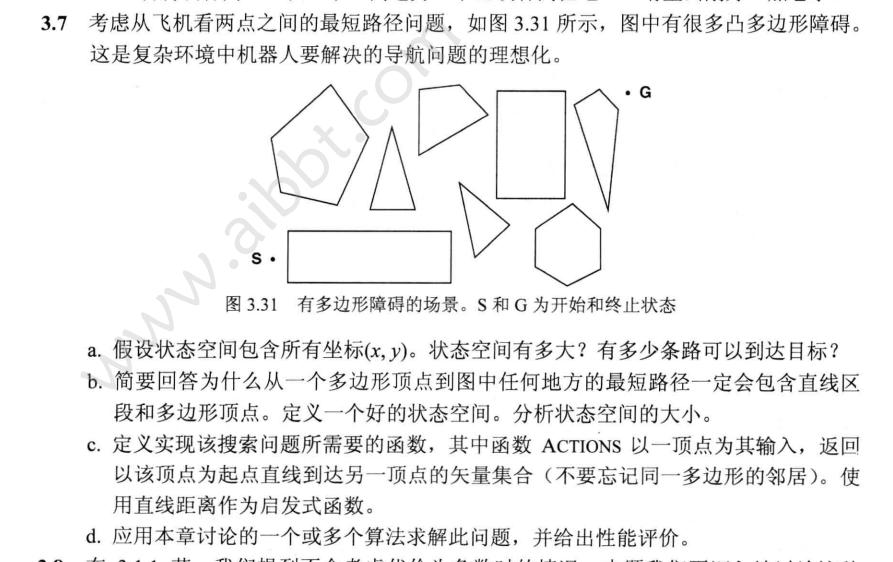
步骤

地图预处理

题中寻路地图包含在很多文字之中，且图中还包含logo，这都直接影响了寻路算法的使用，因此需要将图片转程序易处理的数据结构。预处理后地图如下：

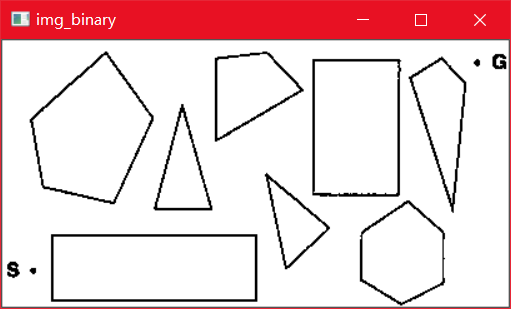
算法思想

A*算法为了在获得最短路径的前提下搜索最少节点，通过不断计算当前节点的附近节点F(N)值来判断下次探索的方向，每个节点的值计算方法为：F(N)=G(N)+H(N)。

其中G(N)是从起点到当前节点N的移动消耗（比如低消耗代表平地、高消耗代表沙漠）；H(N)代表当前节点到目标节点的预期距离，可以用使用曼哈顿距离、欧氏距离等。当节点间移动消耗G(N)非常小时，G(N)对F(N)的影响也会微乎其微，A*算法就退化为最好优先贪婪算法；当节点间移动消耗G(N)非常大以至于H(N)对F(N)的影响微乎其微时，A*算法就退化为Dijkstra算法。

算法步骤

整个算法流程为^[4]：

设定两个集合：open集、close集
将起始点加入open集，其F值为0（设置父亲节点为空）
当open集合非空，则执行以下循环
3.1 在open集中移出一个F值最小的节点作为当前节点，并将其加入close集
3.2 如果当前节点为终点，则退出循环完成任务
3.3 处理当前节点的所有邻居节点，对于每个节点进行以下操作：
- 如果该节点不可达或在close集中则忽略该节点
- 计算该节点的F(N)值，并：如果该节点在open集中且F(N)大于当前F(N)，则选择较小F(N)替换；否则将该节点加入open集
- 将该节点的父节点设置为当前节点
- 将该节点加入open集
搜索结束如果open集为空，则可能搜索到一条路径；如果open集非空，则必然搜索到一条路径，从终点不断遍历其父节点便是搜索路径。

代码实现

使用Python编写A*算法的核心代码为：

class AStar(object):
    '''
    @param      {*} graph   地图
    @param      {*} start   开始节点
    @param      {*} goal    终点
    '''
    def __init__(self, graph, start, goal):
        self.start = start
        self.goal = goal
        self.graph = graph
        # 优先队列储存open集
        self.frontier = PriorityQueue()
        # 初始化起点
        self.frontier.put(start)

    '''
    @description: 绘出最终路径
    '''

    def draw_path(self):
        path = self.goal
        matrix = self.graph.matrix
        while path:
            matrix[path.x][path.y] = 0
            path = path.father

    def run(self):
        plt.ion()
        n = 0
        while not self.frontier.empty():
            n = n + 1
            current = self.frontier.get()
            # 是否为终点
            if current.equal(self.goal):
                self.goal.father = current
                self.draw_path()
                return True
            # 遍历邻居节点
            for next in self.graph.neighbors(current):
                # 计算移动消耗G
                next.g = current.g + self.graph.cost(current, next)
                # 计算曼哈顿距离H
                next.manhattan(self.goal)
                # 如果当前节点未在open集中
                if not next.used:
                    next.used = True
                    # 将探索过的节点设为阴影，便于观察
                    self.graph.matrix[next.x][next.y] = 99
                    # 将当前节点加入open集
                    self.frontier.put(next)
                    # 设置该节点的父节点为当前节点
                    next.father = current
            # 没100次更新一次图像
            if n % 100 == 0:
                plt.clf()
                plt.imshow(self.graph.matrix)
                plt.pause(0.01)
                plt.show()
        return False

寻路结果如下（其中黑实线是算法得出的最优路径，路径旁边的黑色地带是探索过的节点）：

思考

本例中图像共有406×220像素，即有89320个像素点，也就是状态空间共有89320，可选线路最高有893202约为80亿种，虽然经过了简单的地图优化处理，但直接使用A*算法的效率还是很低。要想进一步提高搜索效率，可以引出另外一条定理：给定平面上一个起始点s和一个目标点g，以及若干多边形障碍物P1, P2, P3 ... Pk，由于两点间直线最短，故在所有从s到g的路径中，距离最短的路径的拐点一定在多边形顶点上。基于以上定理，我们可以人工将地图中的多边形顶点进行提取，再用A*算法对提取的顶点进行计算，即可在获得最短路径的同时大大增加了算法的效率。

完整代码

数据结构

from queue import PriorityQueue
import cv2
import math
import matplotlib.pyplot as plt
import fire


class Node(object):
    def __init__(self, x=0, y=0, v=0, g=0, h=0):
        self.x = x
        self.y = y
        self.v = v
        self.g = g  #g值
        self.h = h  #h值
        self.used = False
        self.father = None  #父节点

    '''
    @description: 曼哈顿距离
    @param      {*} endNode 目标节点
    '''

    def manhattan(self, endNode):
        self.h = (abs(endNode.x - self.x) + abs(endNode.y - self.y)) * 10

    '''
    @description: 欧拉距离
    @param      {*} self
    @param      {*} endNode
    @return     {*}
    '''

    def euclidean(self, endNode):
        self.h = int(math.sqrt(abs(endNode.x - self.x)**2 + abs(endNode.y - self.y)**2)) * 30

    '''
    @description: 判断other节点与当前节点是否相等
    @param      {*} other
    '''

    def equal(self, other):
        if self.x == other.x and self.y == other.y:
            return True
        else:
            return False

    '''
    @description: 函数重载，为了满足PriorityQueue进行排序
    @param      {*} other
    '''

    def __lt__(self, other):
        if self.h + self.g <= other.h + other.g:
            return True
        else:
            return False


class Graph(object):
    '''
    @description: 类初始化
    @param      {*} matrix  地图矩阵
    @param      {*} maxW    地图宽
    @param      {*} maxH    地图高
    '''
    def __init__(self, matrix, maxW, maxH):
        self.matrix = matrix
        self.maxW = maxW
        self.maxH = maxH
        self.nodes = []
        # 普通二维矩阵转一维坐标矩阵
        for i in range(maxH):
            for j in range(maxW):
                self.nodes.append(Node(i, j, self.matrix[i][j]))

    '''
    @description: 检查坐标是否合法
    @param      {*} x
    @param      {*} y
    '''

    def checkPosition(self, x, y):
        return x > 0 and x < self.maxH and y > 0 and y < self.maxW and self.nodes[x * self.maxW + y].v > 200

    '''
    @description: 寻找当前节点的邻居节点
    @param      {Node} node 当前节点
    @return     {*}
    '''

    def neighbors(self, node: Node):
        ng = []
        if self.checkPosition(node.x - 1, node.y):
            ng.append(self.nodes[(node.x - 1) * self.maxW + node.y])
        if self.checkPosition(node.x + 1, node.y):
            ng.append(self.nodes[(node.x + 1) * self.maxW + node.y])
        if self.checkPosition(node.x, node.y - 1):
            ng.append(self.nodes[node.x * self.maxW + node.y - 1])
        if self.checkPosition(node.x, node.y + 1):
            ng.append(self.nodes[node.x * self.maxW + node.y + 1])

        if self.checkPosition(node.x + 1, node.y + 1):
            ng.append(self.nodes[(node.x + 1) * self.maxW + node.y + 1])
        if self.checkPosition(node.x + 1, node.y - 1):
            ng.append(self.nodes[(node.x + 1) * self.maxW + node.y - 1])
        if self.checkPosition(node.x - 1, node.y + 1):
            ng.append(self.nodes[(node.x - 1) * self.maxW + node.y + 1])
        if self.checkPosition(node.x - 1, node.y - 1):
            ng.append(self.nodes[(node.x - 1) * self.maxW + node.y - 1])
        return ng

    '''
    @description: 画出结果路径
    '''

    def draw(self):
        cv2.imshow('result', self.matrix)
        cv2.waitKey(0)
        cv2.destroyAllWindows()

    '''
    @description: 计算节点间移动消耗
    @param      {Node} current
    @param      {Node} next
    @return     {*}
    '''

    def cost(self, current: Node, next: Node):
        return 11 if abs(current.x - next.x) + abs(current.y - next.y) > 1 else 10


class AStar(object):
    '''
    @param      {*} graph   地图\n
    @param      {*} start   开始节点
    @param      {*} goal    终点
    '''
    def __init__(self, graph, start, goal):
        self.start = start
        self.goal = goal
        self.graph = graph
        # 优先队列储存open集
        self.frontier = PriorityQueue()
        # 初始化起点
        self.frontier.put(start)

    '''
    @description: 绘出最终路径
    '''

    def draw_path(self):
        path = self.goal
        matrix = self.graph.matrix
        while path:
            matrix[path.x][path.y] = 0
            path = path.father

    def run(self):
        plt.ion()
        n = 0
        while not self.frontier.empty():
            n = n + 1
            current = self.frontier.get()
            # 是否为终点
            if current.equal(self.goal):
                self.goal.father = current
                self.draw_path()
                return True
            # 遍历邻居节点
            for next in self.graph.neighbors(current):
                # 计算移动消耗G
                next.g = current.g + self.graph.cost(current, next)
                # 计算曼哈顿距离H
                next.manhattan(self.goal)
                # 如果当前节点未在open集中
                if not next.used:
                    next.used = True
                    # 将探索过的节点设为阴影，便于观察
                    self.graph.matrix[next.x][next.y] = 99
                    # 将当前节点加入open集
                    self.frontier.put(next)
                    # 设置该节点的父节点为当前节点
                    next.father = current
            # 没100次更新一次图像
            if n % 100 == 0:
                plt.clf()
                plt.imshow(self.graph.matrix)
                plt.pause(0.01)
                plt.show()
        return False

主程序


import cv2
from AStar import Node, AStar, Graph

src_path = "./map.png"
# 读取图片
img_grey = cv2.imread(src_path, cv2.IMREAD_GRAYSCALE)
# 去除水印
img_grey = cv2.threshold(img_grey, 200, 255, cv2.THRESH_BINARY)[1]
# 二值化
img_binary = cv2.threshold(img_grey, 128, 255, cv2.THRESH_BINARY)[1]
img_binary[:][0] = 0
img_binary[:][-1] = 0
img_binary[0][:] = 0
img_binary[-1][:] = 0

start = Node(180, 30)
goal = Node(20, 370)
maxH, maxW = img_binary.shape
graph = Graph(img_binary, maxW, maxH) 
astar = AStar(graph, start, goal)
astar.run()

cv2.imshow('result', graph.matrix)
cv2.waitKey(0)
cv2.destroyAllWindows()

参考文献

好好学习天天引体向上. 寻路算法小结. 简书. [2017-01-09] ↩︎
wier. 深入理解游戏中寻路算法. OSChina. [2017-07-25] ↩︎
云加社区. 最快速的寻路算法 Jump Point Search. InfoQ. [2020-11-29] ↩︎
Amit Patel. Introduction to the A* Algorithm. redblobgames.com. [2014-05-26] ↩︎

posted @ 2022-03-24 14:20 丿风色幻想阅读(1019) 评论(17) 编辑收藏举报

会员力量，点亮园子希望

刷新页面返回顶部

风色幻想