数值计算算法-最小二乘估计的实现与分析
最小二乘估计法(又称最小平方法)用来确定形如函数y(x) = b1x + b0中的b1和b0的估计值,使得y(x)是n个点(x0,y0),...,(xn-1,yn-1)的最佳拟合线。
最佳拟合线采用最小二乘估计法来最小化点(xi, yi)(i=0,...,n-1)同对应点(xi,y(xi))之间的垂直平方距离之和。在这种定义下,每个点(xi, yi)都会尽可能靠近这条线段,因而称为最佳拟合线。
也许最小二乘估计法最重要的应用就是对两个变量之间的线性关系进行推导。假设有一个独立的变量x和一个同x相关的变量y,在没有得到实际的y值时,估计量b1和b0允许在已知x时计算出相对应的y的值。这在当x和y具有统计关系时(不精确的关系)显得尤其有意义。比如,设想一下某个咨询公司每个月雇佣的员工数与该公司收取咨询费的总小时数相关。一般来说,随着公司雇佣更多的员工,公司将得到更多的咨询服务时数。但是,对于咨询时数和员工数之间并没有一个精确的关系存在。与之形成对比的则称为函数关系,函数关系必须是精确的。比如,咨询公司对项目收取的总费用同项目所需要的时长之间就应该是一种函数关系。假设给定项目一个具体的时长,那么公司为此收取的咨询费就应该是一个精确的值,这就体现了它们之间的精确关系。
要理解最小二乘法是如何工作的,先回顾一下两个端点(x1,y1)同(x2,y2)之间的距离r可以定义为:
r=√(x2-x1)2 + (y2-y1)2
由于点(xi,yi)和点(xi,y(xi))有相同的横坐标,因此这两个点之间的线段是垂直的。因此,通过上面的公式,我们知道这两个点之间的距离就是它们的纵坐标差的绝对值。或记为|yi - y(xi)|。这个差就称为yi在xi上的偏差。
考虑一下为什么要用方差来计算b1和b0而不是直接用偏差呢?主要是因为当将误差总和降到最低时,最终得到的联立方程组是线性的。在计算机出现之前,这是最容易解决的问题。另一个原因可以在概率论的基础上做出解释。简单来说,这个概率就是b1和b0相对于(xi,yi)的最佳观测值,它与包含所有(yi - y(xi)2)的总和的负指数成正比。因此,当我们以是减少求偏差平方之和所带来的误差时,同时也会使得b1和b0的估计值最佳化的概率达到最大。还有一个原因是对偏差做开平方处理后,会使得较大的偏差出现的几率变高。由于在正态分布下很少会出现大的偏差实例,因此这就给那些不常出现的偏差值更大的权重。
可以采用下面的公式来计算b1和b0,这里x和y代表n个点的坐标。这些都取自于前面提到过但没给出的联立方程组。公式中出现的符号Σ(sigma)在这里表示求和。
b1 = (nΣxiyi - ΣxiΣyi) / nΣxi2 - (Σxi)2 b0 =( Σyi - b1Σxi ) / n
下图展示了当n = 9时,针对9个点(x0,y0) , ... , (x8,y8)求解b1和b0的过程。计算的结果统计在表中。采用表格中的数据,b1和b0可以通过下面的式子计算得出:
b1 = (9*35.75 - (-0.5)*(-0.5)) / 9*64.75 - (-0.5)2 =0.5519,
b0 = ((-0.5) - 0.5519 * (-0.5)) / 9 = 0.0249
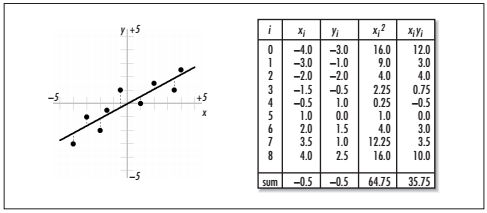
将这些值带入函数y(x) = b1x + b0中,得到y(x) = 0.5519x - 0.0249。用这些点绘制出最佳拟合曲线。如图中所示。从最小二乘估计的角度来看,这是最佳拟合线,再没有别的线段能同这些数据更吻合了。
最小二乘估计的接口定义
lsqe
void lsqe(const double *x, const double *y, int n, double *b1, double *b0);
返回值:无
描述: 采用最小二乘估计法来计算函数y(x) =b1x + b0中的系数b1和b0,这样y(x)将是由参数x和y所指定的点集的最佳拟合线。点集的横坐标由参数x所指定,纵坐标由y所指定。n代表点的个数。该函数返回合适的b1和b0的值。
复杂度: O(n),这里n代表点集中元素的个数。
最小二乘估计的实现与分析
本节给出的最小二乘估计只需要做一些求和计算,并将结果运用到前面介绍过的公式中即可。
首先,分别对所有的xi和yi求和,并将结果分别赋给sumx和sumy。针对所有的xi2和xiyi求和,并将结果分别赋给sumx2和sumxy。一旦完成了计算,接下来就用前面介绍过的公式来计算b1和b0。
函数lsqe的时间复杂度是O(n),这是因为该函数只有一个循环,需要遍历n次才能得出求和的结果,这里n是点集中元素的个数。
示例:最小二乘估计的实现
/* lsqe.c */ #include <math.h> #include "nummeths.h" void lsqe(const double *x, const double *y, int n, double *b1, double *b0) { double sumx, sumy, sumx2, sumxy; int i; /* 计算所需求和 */ sumx = 0.0; sumy = 0.0; sumx2 = 0.0; sumxy = 0.0; for(i=0; i<n; i++) { sumx = sumx + x[i]; sumy = sumy + y[i]; sumx2 = sumx2 + pow(x[i],2.0); sumxy = sumxy + (x[i]*y[i]); } /*最小二乘估计的计算*/ *b1 = (sumxy - ((sumx * sumy)/(double) n)) / (sumx2 - (pow(sumx,2.0)/(double) n)); *b0 = (sumy - ((*b1)*sumx)) / (double )n; return ; }



 浙公网安备 33010602011771号
浙公网安备 33010602011771号