排序算法的C语言实现(下 线性时间排序:计数排序与基数排序)
计数排序
计数排序是一种高效的线性排序。
它通过计算一个集合中元素出现的次数来确定集合如何排序。不同于插入排序、快速排序等基于元素比较的排序,计数排序是不需要进行元素比较的,而且它的运行效率要比效率为O(nlgn)的比较排序高。
计数排序有一定的局限性,其中最大的局限就是它只能用于整型或那么可以用整型来表示的数据集合。原因是计数排序利用一个数据的索引来记录元素出现的次数,而这个数组的索引就是元素的数值。例如,如果整数3出现过4次,那么4将存储到数组索引为3的位置上。同时,我们还需要知道集合中最大整数的值,以便于为数组分配足够的空间。
除了速度之外,计数排序的另一个优点就是非常稳定。稳定的排序能使具有相同数值的元素具有相同的顺序,就像它们在原始集合中表现出来的一样。在某些情况下这是一个重要的特性,可以在基数排序中看到这一点。
计数排序的接口定义
ctsort
int ctsort(int *data, int size, int k);
返回值:如果排序成功,返回0;否则,返回-1;
描述: 利用计数排序将数组data中的整数进行排序。data中的元素个数由size决定。参数k为data中最大的整数加1。当ctsort返回时,data中包含已经排序的元素。
复杂度:O(n+k),n为要排序的元素个数,k为data中最大的整数加1。
计数排序的实现与分析
计数排序本质上是通过计算无序集合中整数出现的次数来决定集合应该如何排序的。
在以下说明的实现方法中,data初始包含size个无序整型元素,并存放在单块连续的存储空间中。另外需要分配存储空间来临时存放已经排序的元素。在ctsort返回时,得到的有序集合将拷贝加data。
分配了存储空间以后,首先计算data中每个元素出现的次数。这些结果将存储到计数数组counts中,并且数组的索引值就是元素本身。一旦data中每个元素的出现次数都统计出来后,就要调整计数值,使元素在进入有序集合之前,清楚每个元素插入的次数。用元素本身的次数加上它前一个元素的次数。事实上,此时counts包含每个元素在有序集合temp中的偏移量。
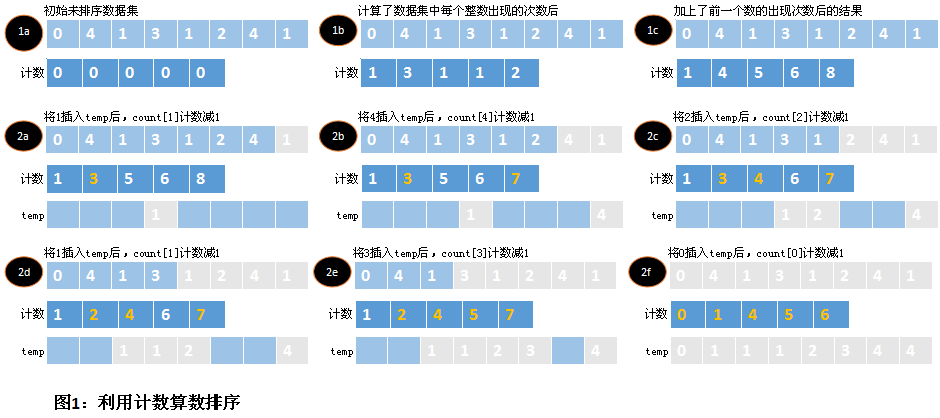
要完成排序,还必须按照元素在temp中的偏移量放置元素。当temp更新时,每个元素的计数要减1,这样,在data中出现不止一次的元素在temp中也会出现不止一次,这样保持同步。
计数排序的时间复杂度为O(n+k),其中n为要排序的元素个数,k为data中最大的整数加1。这是由于计数排序包含三个循环,其中两个的运行时间正比于n,另一个的运行时间正比于k。对于空间上来说,计数排序需要两个大小为n的数组,一个大小为k的数组。
示例:计数排序的实现
/*ctsort.c*/ #include <stdlib.h> #include <string.h> #include "sort.h" /*ctsort 计数排序函数*/ int ctsort(int *data, int size, int k) { int *counts, *temp; int i,j; /*为计数器数组分配空间*/ if((counts = (int *)malloc(k * sizeof(int))) == NULL) return -1; /*为已排序元素临时存放数组分配空间*/ if((temp = (int *)malloc(size * sizeof(int))) == NULL) return -1; /*初始化计数数组*/ for(i = 0; i < k; i++) { counts[i] = 0; } /*统计每个元素出现的次数(counts的下标索引即是要统计的元素本身)*/ for(j=0; j<size; j++) counts[data[j]]=counts[data[j]] + 1; /*将元素本身的次数加上它前一个元素的次数(得到元素偏移量)*/ for(i = 1; i < k; i++) counts[i]=counts[i] + counts[i-1]; /*关键代码:使用上面得到的计数数组去放置每个元素要排序的位置*/ for(j = size -1; j >= 0; j--) { temp[counts[data[j]]-1] = data[j]; /*counts的值是元素要放置到temp中的偏移量*/ counts[data[j]] = counts[data[j]] - 1; /*counts的计数减1*/ } /*将ctsort已排序的元素从temp拷贝回data*/ memcpy(data,temp,size * sizeof(int)); /*释放前面分配的空间*/ free(counts); free(temp); return 0; }
基数排序
基数排序是另外一种高效的线性排序算法。
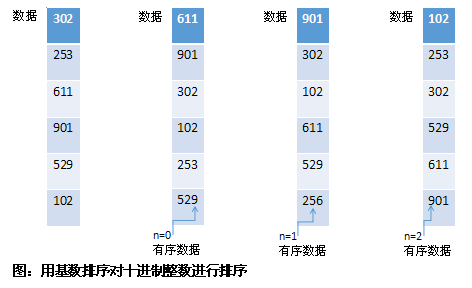
其方法是将数据按位分开,并从数据的最低有效位到最高有效位进行比较,依次排序,从而得到有序数据集合。
我们来看一个例子,用基数排序对十进制数据{15,12,49,16,36,40}进行排序。在对个位进行排序之后,其结果为{40,12,15,16,36,49},在对十位进行排序之后,其结果为{12,15,16,36,40,49}。
有一点非常重要,在对每一位进行排序时其排序过程必须是稳定的。一旦一个数值通过较低有效位的值进行排序之后,此数据的位置不应该改变,除非通过较高有效位的值进行比较后需要调整它的位置。例如,在上述的例子中,12和15的十位都是1,当对其十位进行排序时,一个不稳定的排序算法可能不会维持其在个数排序过程中的顺序。而一个稳定的排序算法可以保证它们不重新排序。基数排序会用到计数排序,对于基数排序来说,除了稳定性,它还是一种线性算法,且必须知道每一位可能的最大整数值。
基数排序并不局限于对整数进行排序,只要能把元素分割成整型数,就可以使用基数排序。例如,可以对一个以28为基数字符串进行基数排序;或者,可以对一个64位的整数,按4位以216为基数的值进行排序。具体该选择什么值作为基数取决于数据本身,同时考虑到空间的限制,需要将pn+pk最小化。(其中p为每个元素的位数,n为元素的个数,k为基数)。一般情况下,通常使k小于等于n。
基数排序的接口定义
rxsort
int rxsort(int *data, int size, int p, int k);
返回值:如果排序成功,返回0;否则返回-1。
描述:利用计数排序将数组data中的整数进行排序。数组data中整数的个数由size决定。参数p指定每个整数包含的位数,k指定基数。当rxsort返回时,data包含已经排序的整数。
复杂度:O(pn+pk),n为要排序的元素个数,k为基数,p为位的个数。
基数排序的实现与分析
基数排序实质上是在元素每一位上应用计数排序来对数据集合排序。在以下介绍的实现方法中,data初始包含size个无序整型元素,并存放在单块连续的存储空间中。当rxsort返回时,data中的数据集完全有序。
如果我们理解了计数排序的方法,那么基数排序也就非常简单了。单个循环控制正在进行排序的位置。从最低位开始一个位置一个位置地应用计数排序来不断调整元素。一旦调整完了最高有效位的数值,排序过程就完成了。
获取每位数值的简单方法就是使用幂运算和模运算。这对整数来说特别有效,但不同的数据类型需要使用不同的方法。有一些方法可能需要考虑机器具体细节,例如字节顺序和字对齐等。
毫无疑问,基数排序的时间复杂度取决于它选择哪种稳定排序来对数值进行排序。由于基数排序对每个p位置的位数值使用计数排序,因此基数排序消耗的运行时间是计数排序的p倍,即O(pn+pk)。其对空间的要求与计数排序一样:两个大小为n的数组,一个大小为k的数组。
示例:基数排序的实现
/*rxsort.c*/ #include <limits.h> #include <math.h> #include <stdlib.h> #include <string.h> #include "sort.h" /*rxsort*/ int rxsort(int *data, int size, int p, int k) { int *counts, *temp; int index, pval, i, j, n; /*为计数器数组分配空间*/ if((counts = (int *)malloc(k * sizeof(int))) == NULL) return -1; /*为已排序元素集分配空间*/ if((temp = (int *)malloc(size * sizeof(int))) == NULL) return -1; /*从元素的最低位到最高位开始排序*/ for(n=0; n<p; n++) { /*初始化计数器*/ for(i=0; i<k; i++) count[i] = 0; /*计算位置值(幂运算k的n次方)*/ pval = (int)pow((double)k,(double)n); /*统计当前位上每个数值出现的次数*/ for(j=0; j<size; j++) { index = (int)(data[j] / pval) % k; counts[index] = counts[index]+1; } /*计算偏移量(本身的次数加上前一个元素次数)*/ for(i=1; i<k; i++) counts[i] = counts[i] + counts[i-1]; /*使用计数器放置元素位置*/ for(j=size-1; j>=0; j--) { index = (int)(data[j] / pval) % k; temp[counts[index]-1] = data[j]; counts[index] = counts[index] - 1; } /*将已排序元素拷贝回data*/ memcpy(data, temp, size*sizeof(int)); } /*释放已排序空间*/ free(counts); free(temp); return 0; }




 浙公网安备 33010602011771号
浙公网安备 33010602011771号