数据结构 图的定义和搜索方法(清晰图解)
在计算机科学领域中,图是最为灵活的数据结构之一。
一般来说,图在定义对象之间的关系或联系这类问题上能够作为一种模型来帮助我们。
图中的对象可以是具体的,比如网络中的结点;也可以是不具体的,比如数据库中的业务或系统中的状态。相同点是对象之间的关系和联系。网络上的结点是物理上相连接的,系统中状态之间的关系可能只是简单地表示为了达到下一个状态在当前所做出的决策。无论什么情况,图的模型都很有用,能够解决许多有趣的问题。
图的组成:图由两种类型的元素组成,顶点和边。
顶点代表对象,边则建立起对象之间的关系或关联。
图的有向:图要么是有向的,要么是无向的。
在有向图中,边是由两个顶点组成的有序对,具有特定的方向。形象地说,有向图可以由顶点和带方向的箭头所组成的圈绘制出来。
有时候,有向图的边也称为弧。
在无向图中,边是没有方向的,因此,无向图的边就直接用线段来代替箭头表示。
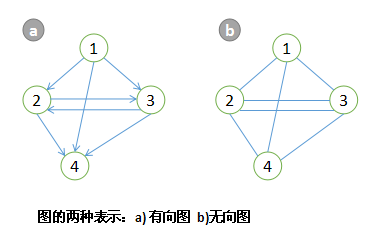
图的正式表示法:G=(V , E),这里V代表顶点的集合,面E和V之间是一种二元关系。
在有向图中,如果某条边是从顶点u开始到顶点v结束,则E包含有序对(u,v)。比如上图中,V={1,2,3,4},而E={(1,2),(1,3),(1,4),(2,3),(2,4),(3,2),(3,4)}。
但是按照惯例,在图中表示边的集合时,用圆括号而不是大括号。
在无向图中,由于边(u,v)和(v,u)是一样的意思,因此在E中只需要记录其中一个就可以了。因此,在上图的b中,V={1,2,3,4},而E={(1,2),(1,3),(1,4),(2,3),(2,4),(3,4)}。
在有向图中,边可能会指回同一顶点,但在无向图中则不会出现这种情况。
图中的两个重要关系:邻接(adjacency)和关联(incidence)。
邻接是两个顶点之间的一种关系。如果图包含边(u,v),则称顶点v和顶点u邻接。在无向图中,这也暗示了顶点u和顶点v邻接。换句话说,在无向图中邻接关系是对称的。
而在有向图中则并非如此,比如上图a中,顶点2与顶点1相邻接,但顶点1并不与顶点2相邻接。另一方面,顶点2和顶点3则互为邻接。
如果一幅图中的每一个顶点都与其他顶点相邻接,则称这幅图是完全图。
关联是指顶点和边之间的关系。在有向图中,边(u,v)从顶点u开始关联到顶点v,或者相反,从顶点v开始关联到顶点u。因此,在上图a中,边(1, 2)从顶点1开始关联到顶点2。
在有向图中,顶点的入度指的是以该顶点为终点的边的数目。而顶点的出度指的是以该顶点为起点的边的数目。
在无向图中,边(u,v)与顶点u和v相关联,而顶点的度就是与该顶点相关联的边的数目。
图的路径:路径是依次遍历顶点序列之间的边所形成的轨迹。
正式的说法是,顶点u到另一个顶点u‘的路径由顶点序列<v0,v1,v2,...vk>组成,使得u=v0且u'=vk,对于i=1,2,...,k,所有的(vi-1,vk)均属于E。这样的一条路径包含边
(v0,v1),(v1,v2),...(vk-1,vk),且长度为k。
如果存在一条从u到u’的路径,则称u‘从u是可达的。
没有重复顶点的路径称为简单路径。
环:是指路径包含相同的顶点两次或两次以上。
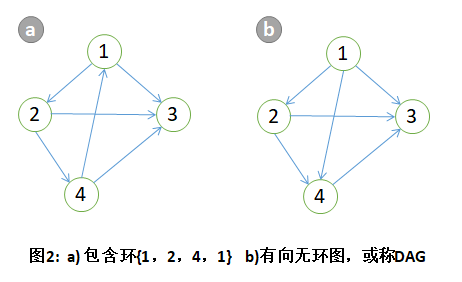
也就是说,在有向图的一条路径中, 如果从某个顶点出发,最后能够驾到该顶点,则该路径是环。图2中包含环{1,2,4,1}。
正式的说法是,在有向图中,如果v0=vk,且路径包含至少一条边,则该路径组成一个环。
在无向图中,有路径<v0,v1,v2,...,vk>,如果有v0=vk且从v1到vk中没有重复的顶点,则该路径组成一个环。
没有环的图称为无环图。有向无环图有特殊的名称,叫做DAG(Directed Acyline Graph)。
联通性:连通性是图中的一个重要概念。对于无向图而言,如果它的每个顶点都能通过某条路径到达其他顶点,那么我们称它为连通的。
如果该条件在有向图中同样成立,则称该图是强连通的。
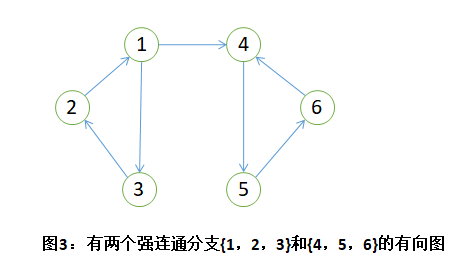
尽管无向图可能不是连通的,但它仍然可能包含连通的部分,这部分称为连通分支。如果有向图中只有部分是强连通的,则该部分称为强连通分支。如图3。
某些特定的于保持图或连通分支的连通性有特殊重要的意义。如果移除某个顶点将使得图或分支失去连通性,则称该顶点为关结点。
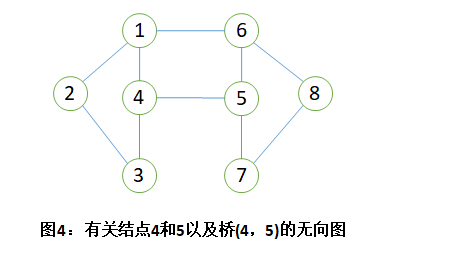
如图4,顶点4和5都是关结点因为如果它们中的任意一个被移除,图就变成非连通的了。移除这些顶点后,图中拥有两个连通分支{1,2,3}和{6,7,8}。
如果移除某条边会使得图失去连通性,则称该边为桥。没有关结点的连通图称为双连通图。尽管图本身可能不是双连通的,但它仍然可能包含双连通分支。
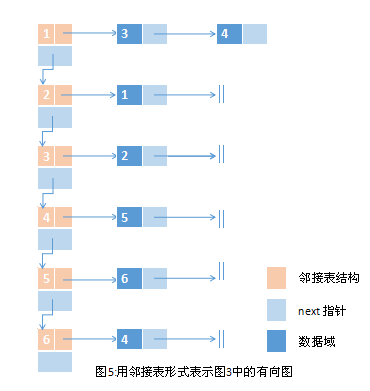
图的表示方法:最常用来表示图的方法是采用邻接表表示形式,邻接表按照链表的方式组织起来。
链表中的每一个结构都包含两个成员:一个顶点和与该顶点邻接的顶点所组成的一个邻接表。
在图G=(V,E)中,如果V中的两个顶点u和v组成E中的边(u,v),则顶点v包含在顶点u的邻接表中。因而,在有向图中,所有邻接表中的顶点总数同总的边数相等。
在无向图中,由于边(u,v)暗含了边(v,u),因此顶点v包含在顶点u的邻接表中,而顶点u而包含在顶点v的邻接表中。因而,在这种情况下所有邻接表中的顶点总数是总边数的两倍。
通常,邻接表多用于稀疏图中,稀疏图是指边数相对来说较少的图。稀疏图非常普遍。但是如果图非常的稠密,就应该选择邻接矩阵表示方式来表示稠密图了。需要占用O(VE)的空间。
搜索方法:广度优先搜索和深度优先搜索
广度优先搜索
广度优先搜索在进一步探索图中的顶点之前,先访问当前顶点的所有邻接顶点。
这种查找方法在很多应用中都非常有用,包括查找出最小生成树和最短路径问题。
开始前,优先选择一个起始顶点并将其涂灰,而其他顶点为白色。把起始顶点置于一个队列中。
该算法按照如下方式处理:对于队列中的每一个顶点(初始状态下只有起始顶点),从队列首部选出这个顶点并找出每一个与之相邻接的顶点。
将找到的邻接顶点入队到队列的末尾。我们将已经访问过的顶点涂黑,而还没访问过的顶点则是白色。如果顶点的颜色是灰色,表示已经发现它了,并把它入队到队列末尾。
如果顶点的颜色是白色,表示还没有发现它,将按照同样的方法继续处理队列中的下一个邻接顶点。
一旦所有的邻接顶点都已经找到,就将队列头的顶点出队并将其涂黑,表示我们已经完成了对其的查找。我们继续这个步骤直到队列为空,此时,从起始顶点开始可达的所有顶点都已经涂黑了。
图6演示了一个有向图的广度优先搜索过程,广度优先搜索也能应用于无向图中。
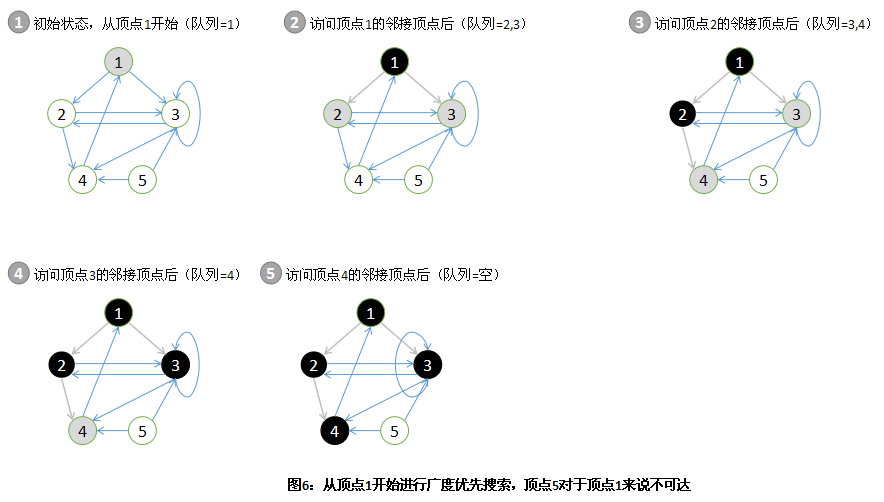
除了简单地访问顶点外,广度优先搜索还可以用来跟踪记录一些有用的信息。比如,在到达每个顶点之前,可以记录已经遍历过的顶点个数,在一个每条边都没有权重的图中,由这些顶点组成的路径往往就是访问每个顶点的最短路径。在图6中,从顶点1到顶点2或顶点3的最短路径只包含1跳,当找到顶点2和3时就记录下来。从顶点1到顶点4的最短路径包含两跳:其中1跳已经在找到顶点2时记录下来了,另一跳则在从顶点2出发到顶点4时记录下来。
也可以采用广度优先搜索法来生成一颗广度优先树。广度优先树是用来维护我们发现的每个顶点的祖先结点信息的数据结构。由于顶点只能被发现1次(当其涂黑时),它只有惟一一个祖先或父结点。在图6中灰色线段标注的边就是广度优先树的枝干。
深度优先搜索
深度优先搜索在搜索过程中每当访问到某一个顶点后,需要递归地访问此顶点的所有未访问过的相邻顶点。因而,这种搜索将尽可能深地持续探索,直到无法继续为止。这种策略使得深度优先搜索在很多应用中非常有用,包括环检测以及拓扑排序。
搜索开始前,将每个顶点涂为白色,并选择一个作为起始点。该算法执照如下的方式进行处理:首先选择一个起始顶点,涂为灰色,表示还未发现它。
然后从该顶点的邻接并且未发现顶点集合中选择一个新顶点,继续这个过程,直到所选的顶点没有其他的白色邻接顶点为止,此时已经到达了最深的程度。因而,将当前选择的顶点涂黑,表示完成了对其的探索,然后回溯到该顶点的上一个顶点,继续探索其余的白色邻接顶点。
继续这个步骤,直到所选择的初始顶点已经没有白色的邻接顶点为止。这个过程仅访问了从初始顶点开始可达的顶点。因此,整个处理过程必须在图中的每一个顶点上重复。
如图7所示,如果缺少重复这个步骤,将不会访问到顶点4。当我们在一个已经涂黑的顶点上重复该过程时,搜索过程将立刻停止,然后我们继续移动到下一个顶点。图7在有向图上展示了深度优先搜索的过程,深度优先搜索也能应用在无向图上。
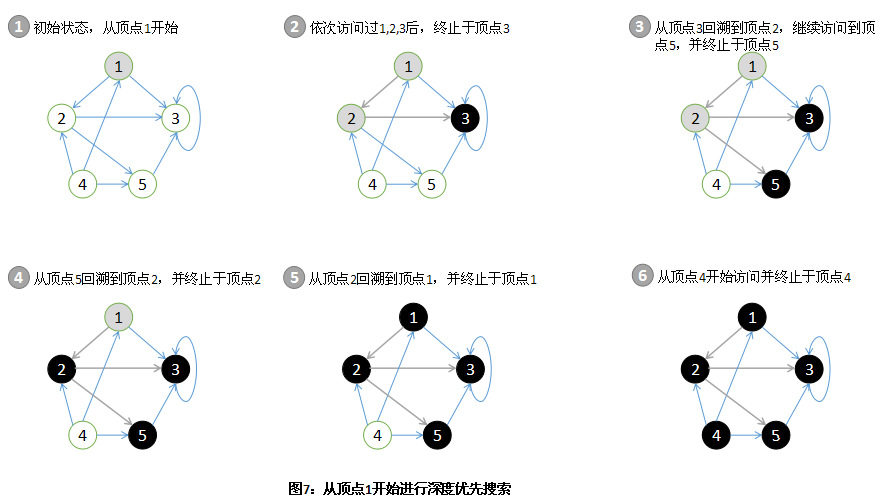
除了只搜索顶点外,深度优先搜索也可以用来记录一些有用的信息。比如,可以记录发现和终止于每个顶点的次数。深度优先搜索也可以用来构建一个深度优先生成森林。
深度优先生成森林是树的集合,每一棵树用来维护搜索到的每个顶点的祖先结点。由于顶点只能发现一次(当将其涂黑时),因此每个顶点都只有唯一的祖先结点(或父结点)。每棵树都包含搜索过程中发现的与该顶点唯一相连的结点。在图7中,以灰色线段标注的边就是树的枝干。




 浙公网安备 33010602011771号
浙公网安备 33010602011771号