数据结构-堆 接口定义与实现分析（详细注释与图解）

如果想了解堆的概念，可以点击此处查看前面关于堆的定义的随笔。

堆的操作接口包括初始化堆、销毁堆、向堆中插入元素、从堆顶移除元素、堆的结点个数。

我们用heap来命名一个堆。下面是对以上接口的定义：

heap_init

---

 void heap_init(Heap *heap,int (*compare)(const void key1,const void key2),void (*destroy)(void *data));

返回值：无

描述：初始化堆heap。

在对堆执行其他操作之前，必须要对其进行初始化。

函数compare用来比较堆中的结点大小，如果堆为最大值堆，当key1>key2时，函数返回1；当key1=key2时，函数返回0；当key1<key2时，函数返回-1。在最小值堆中返回值正好相反。

函数指针destroy，通过调用heap_deatroy来释放动态分配的内存空间。如果堆中的数据不需要释放，那么destroy应该指向NULL。

复杂度：O(1)

heap_destroy

---

 void heap_destroy(Heap *heap);

返回值：无

描述：销毁堆heap。

在调用heap_destroy之后不再允许进行其他操作。

heap_destroy会删除堆中的所有结点，在删除的同时调用heap_init中的destroy所指向的销毁函数（此函数指针不为NULL）。

复杂度：O(n)，n代表堆中的结点个数。

heap_insert

---

 int heap_insert(Heap *heap,const void *data);

返回值：如果插入元素成功则返回0，否则返回-1。

描述：向堆heap中插入一个结点。

新结点包含一个指向data的指针，只要结点仍然存在于堆中，此指针就一直有效。与data有关的内存空间将由函数的调用者来管理。

复杂度：O(lg n)，n代表堆中的结点个数。

heap_extract

---

 int heap_extract(Heap *heap,void **data);

返回值：如果结点释放成功则返回0，否则返回-1。

描述：从堆heap中释放堆顶部的结点。

返回时，data指向被释放结点中存储的数据。与data相关的内存空间将由函数的调用者来管理。

复杂度：O(lg n)，n代表堆中的结点个数。

heap_size

---

 int heap_size(const Heap *heap);

返回值：堆中结点的个数。

描述：这是一个获取堆heap中结点个数的宏。

复杂度：O(1)。

 

下面来分析一下如何实现堆：

我们用来叉树来实现堆，将其结点按照树的层次结构存放在一个数组中。我们令Heap作为堆的数据结构，此结构体包含4个成员：

1、size指明堆中的结点个数；2、compare与3、destroy是用于封闭传入heap_init的函数的指针；4、tree是堆中存储结点的数组。

堆的头文件示例如下：

/*heap.h*  堆的头文件/
#ifndef HEAP_H
#define HEAP_H

/*定义堆的数据结构体*/
typedef struct Heap_
{
    int size;
    
    int (*compare)(const void *key1,const void *key2);
    void (*destroy)(void *data);
    
    void **tree;
}Heap;

/*公共接口部分*/
void heap_init(Heap *heap,int (*compare)(const void *key1,const void key2),void (*destroy)(void *data));
void heap_destroy(Heap *heap);
int heap_insert(Heap *heap,const void *data);
int heap_extract(Heap *heap,void **data);

#define heap_size(heap)((heap)->size)

#endif // HEAP_H

堆的实现示例如下：

/*heap.c*/
#include <stdlib.h>
#include <string.h>

#include "heap.h"
/*定义heap执行中需要使用的私有宏*/
#define heap_parent(npos) ((int)(((npos)-1)/2))  /*npos的父结点*/
#define heap_left(npos) (((npos)*2)+1)           /*npos的左兄弟结点*/
#define heap_right(npos) (((npos)*2)+2)          /*npos的右兄弟结点*/

/*heap_init 堆的初始化*/
void heap_init(Heap *heap,int (*compare)(void *key1,void *key2),void (*destroy)(void *data))
{
    /*只需要将size设为0，destroy成员指向destroy，将tree指针设置为NULL*/
    heap->size = 0;
    heap->compare = compare;
    heap->destroy = destroy;
    heap->tree = NULL;

    return ;
}
/*heap_destroy  销毁堆*/
void heap_destroy(Heap *heap)
{
    int i;
    /*移除堆中所有的结点*/
    if(heap->destroy != NULL)
    {
        for(i=0; i<heap_size(heap);i++)
        {
            /*调用用户自定义函数释放动态分配的数据*/
            heap->destroy(heap->tree[i]);
        }
    }
    /*释放为堆分配的空间*/
    free(heap->tree);

    memset(heap,0,sizeof(Heap));
    return;
}

/*heap_insert  向堆中插入结点*/
int heap_insert(Heap *heap,const void *data)
{
    void *temp;
    int  ipos;
         ppos;

    /*为结点分配空间*/
    if((temp = (void **)realloc(heap->tree,(heap->size(heap)+1)*sizeof(void *))) == NULL)
    {
        return -1;
    }
    else
    {
        heap->tree = temp;
    }
    /*将结点插入到堆的最末端*/
    heap->tree[heap_size(heap)] = (void *)data;
    /*将新结点向上推动，恢复堆的排序特点*/
    ipos = heap_size(heap);    /*堆结点数的数值*/
    ppos = heap_parent(ipos);  /*ipos位置结点的父结点*/

    /*如果堆不为空，并且末位结点大于其父结点，则将两个结点进行交换*/
    while(ipos>0 && heap->compare(heap->tree[ppos],heap->tree[ipos])<0)
    {
        /*交换末端结点与其父结点的位置*/
        temp = heap->tree[ppos];
        heap->tree[ppos] = heap->tree[ipos];
        heap->tree[ipos] = temp;

        /*将定位结点向上移动一层，以继续执行堆排序*/
        ipos = ppos;
        ppos = heap_parent(ipos);
    }

    /*堆插入与排序完成，调整堆的结点数量值*/
    heap->size++;

    return 0;
}

/*heap_extract 释放堆顶部的结点*/
int heap_extract(Heap *heap,void **data)
{
    void *save,
         *temp;
    int  ipos,lpos,rpos,mpos;

    /*不允许从空的堆中释放结点*/
    if(heap->size(heap) == 0)
        return -1;

    /*释放堆顶部的结点*/
    /*首先将data指向将要释放结点的数据*/
    *data = heap->tree[0]

    /*将save指向未位结点*/
    save = heap->tree[heap_size(heap)-1];

    if(heap_size(heap)-1 > 0)
    {   /*为堆分配一个稍小一点的空间*/
        if((temp = (void **)realloc(heap->tree,(heap_size(heap)-1)*sizeof(void *)))==NULL)
        {
            return -1;
        }
        else
        {
            heap->tree = temp;
        }
        /*调整堆的大小*/
        heap->size--;
    }
    else
    {   /*只有一个结点，释放并重新管理堆，并返回*/
        free(heap->tree);
        heap->tree = NULL;
        heap->size = 0;
        return 0;
    }
    /*将末位结点拷贝到根结点中*/
    heap->tree[0] = save;

    /*重新调整树的结构*/
    ipos = 0;                /*顶元素*/
    lpos = heap_left(ipos);  /*左子结点*/
    rpos = heap_right(ipos); /*右子结点*/

    /*父结点与两个子结点比较、交换，直到不再需要交换为止，或者结点到达一个叶子位置*/
    while(1)
    {
        /*选择子结点与当前结点进行交换*/
        lpos = heap_left(ipos);
        rpos = heap_right(ipos);
        /*父结点与左子结点位置不正确,左子结点大于其父结点*/
        if(lpos < heap_size(heap) && heap->compare(heap->tree[lpos],heap->tree[ipos])>0)
        {
            mpos = lpos;  /*将左子结点的位置赋给mpos(最大位置)*/
        }
        else
        {
            mpos = ipos;
        }

        if(rpos < heap_size(heap) && heap->compare(heap->tree[rpos],heap->tree[mpos])>0)
        {
            mpos = rpos;
        }

        /*当mpos和ipos相等时，堆特性已经被修复,结束循环*/
        if(mpos == ipos)
        {
            break;
        }
        else
        {
            /*交换当前结点与被选中的结点的内容*/
            temp = heap->tree[mpos];
            heap->tree[mpos] = heap->tree[ipos];
            heap->tree[ipos] = temp;

            /*下移一层，以继续执行堆排序*/
            ipos = mpos;
        }
    }
    return 0;
}

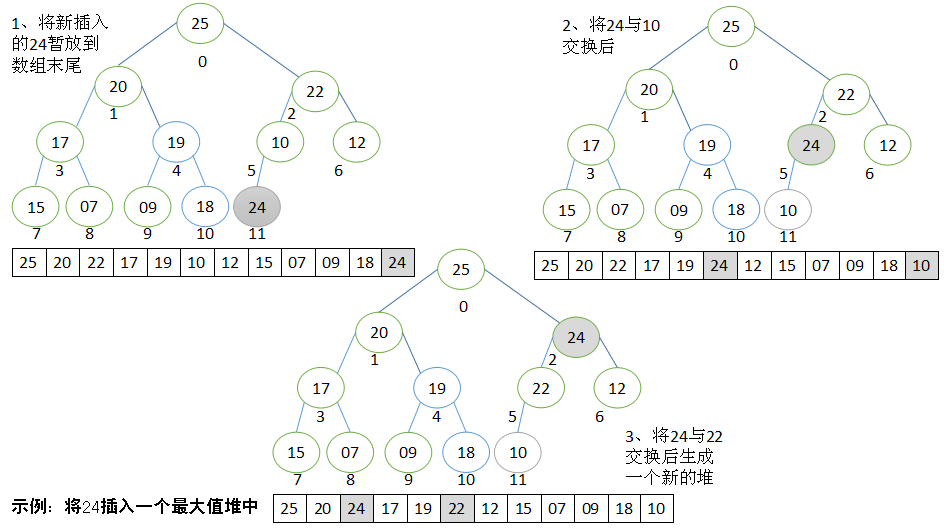
 下图是heap_insert，向最大值堆中插入结点的过程图解示例

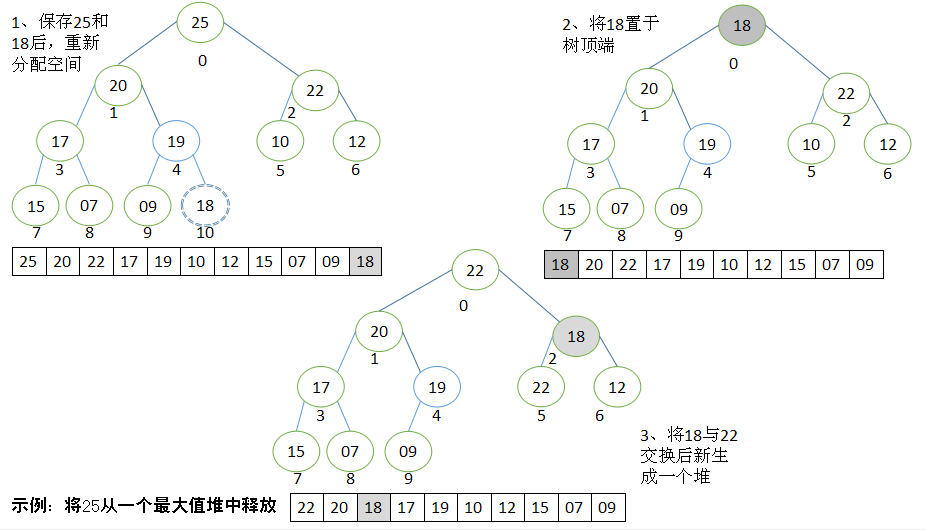
下图是将一个元素从最大值堆中释放的过程图解示例：