二叉搜索树的实现源码(源码较长,请慎入)
实现二叉搜索树的一种好方法是利用二叉树抽象数据类型。
我们以BisTree这个名称来代表二叉搜索树这种数据结构。通过typedef方式将BisTree(二叉搜索树)实现为BiTree(二叉树)的别名。
采用typedef方法使得二叉搜索树具有了某种程度的多态能力,如同栈和队列一样。这意味着除了专属于二叉搜索树的操作外,还可以在其上执行属于二叉树的操作。
数据结构AvlNode代表树中的结点,AvlNode包含3个成员:
data是存储在结点中的数据;hidden用来标识结点是否已经移除;factor则代表该结点的平衡因子。
我们使用标识符来标识平衡因子可能的值:AVL_LEFT_HEAVY定义为1,AVL_BALANCED定义为0,AVL_RGT_HEAVY定义为-1。
示例代码1:二叉搜索树抽象数据类型的头文件
/*bistree.h*/ #ifndef BISTREE_H #define BISTREE_H #include "bitree.h" /*定义平衡因子的标识符*/ #define AVL_LFT_HEAVY 1 #define AVL_BALANCED 0 #define AVL_RGT_HEAVY -1 /*定义AVL树中节点的数据结构*/ typedef struct AvlNode_ { void *data; int hidden; int factor; }AvlNode; /*通过typedef方式将BisTree(二叉搜索树)实现为BiTree(二叉树)*/ typedef BiTree BisTree; /*公用接口部分*/ void bistree_init(BisTree *tree,int (*compare)(const void *key1,const void *key2),void(*destroy)(void *data));
void bistree_destroy(BisTree *tree);
int bistree_insert(BisTree *tree,const void *data); int bistree_remove(BisTree *tree,const void *data); int bistree_lookup(BisTree *tree,void **data); #define bistree_size(tree)((tree)->size) #endif // BISTREE_H
bistree_init
该操作用来初始化一棵二叉树。由于二叉搜索树实际上也是一棵二叉树,因此调用bitree_init来完成初始化工作。这里需要显示地将compare成员设置为指定的比较函数,该成员在二叉树中并没有使用到。
bistree_init的时间复杂度和bitree_init一样都是O(1)。
bistree_destroy
该操作用来销毁一棵二叉树。为了实现该操作,引入两个额外的辅助函数destroy_left和destroy_right。这两个函数按照递归的方式销毁某个结点下方的左右子树。针对二叉搜索树,需要单独的析构函数来销毁AvlNode中数据成员所引用的空间以及AvlNode结构体本身所占用的资源。
bistree_destroy的时间复杂度同bitree_destroy一样,都是O(n),这里的n代表树中的结点个数。
bistree_insert
该操作将一个结点插入二叉搜索树中。该操作按照递归的方式调用bitree_insert来找到结点应该插入的位置。一旦插入结点,就需要更新相关结点的平衡因子,更新操作在递归的回归过程中完成。如果在处理的过程中有任何结点的平衡因子绝对值为2,都需要执行一次旋转。
从检查是否将结点插入空树开始,如果是这种情况,简单的将结点设为根结点,并设它的平衡因子为AVL_BALANCED。
否则,将待插入结点的数据与当前结点的数据相比较,以此来判断需要往哪个方向移动(左子树还是右子树)。当要插入的结点数据小于当前结点的数据时,递归调用该函数使我们移动到左边。当待插入结点的数据大于当前结点的数据时,递归调用该函数将使我们移动到右边。一旦找到了插入的位置,就动态分配一个AvlNode结构体,并将其插入树中,作为当前结点的子结点。
如果待插入结点的数据恰好与某个隐藏的结点的数据一致(由于执行了移除操作,使结点成为隐藏的,但并未真正移除),就销毁当前结点中的数据,将新的数据插入到原来的位置上,并标识该结点不再为隐藏的。在这种情况下不需要再平衡树。
除此之外,替换了之前是隐藏的结点后,下一步需要评估树的平衡性受到的影响,这样如果有必要的话可以对其修复。不论结点插入左边还是右边,都用balanced来表示插入操作是否破坏了树的平衡性。调整当前结点的平衡因子反过来可能会导致该结点上层的平衡因子被打乱。因此,每次调用insert操作时,如果balanced为0,就遍历树当前这一层的所有结点,并更新结点的平衡因子。一旦发现没有结点需要更新了,就将balanced设置为1,以此表示之前的操作已经完成。
switch语句决定如何更新平衡因子,也决定何时应该执行旋转操作。实际用来执行旋转操作的函数要么是rotate_left要么是rotate_right,它们决定旋转的类型:如果调用rotate_left则是LL或者LR;如果调用rotate_right则是RL或RR。由于旋转操作会改变结点的平衡因子,因此每个旋转函数也会修正平衡因子。
和插入一颗完全平衡的二叉树中一样,它们的时间复杂度都是O(lgn)。
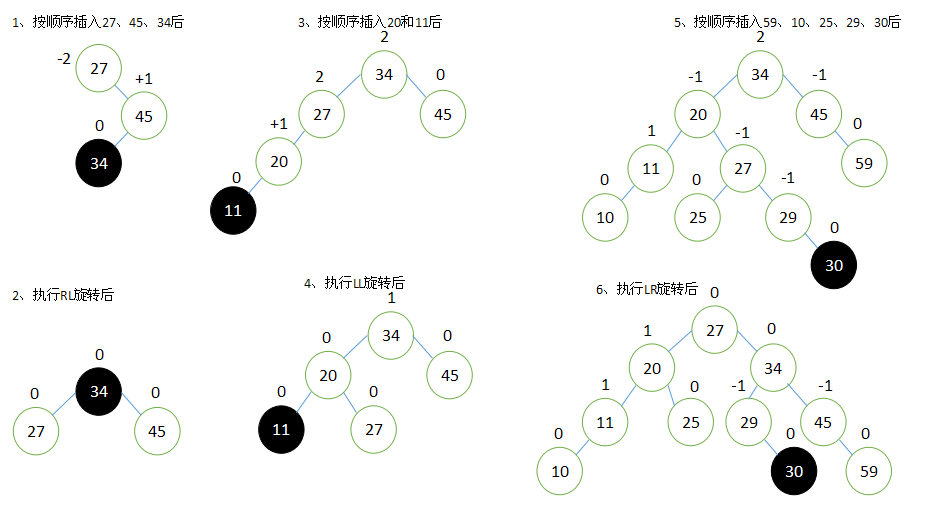
结合下图可以更好的理解更新平衡因子和执行旋转操作:
bistree_remove
该操作将一个节点从二叉搜索树中移除。但它只是将结点隐藏起来而不是真正的移除,我们称之为“惰性移除”。
要隐藏一个结点,将AvlNode结构中的hidden成员设置为1。如果稍后插入同样的数据,只需简单的将hidden成员再次设置为0。
如果移除的结点数目很大,可能就需要考虑将结点真正的移除并重新调整树的结构。
要定位隐藏的结点,以递归的方式调用hide,直到找到目标为止。一旦将结点隐藏了,就没有必要重新平衡树了,因为并没有对树的结构做任何修改。因此,直接将balanced值设置为1。
从AVL树中移除结点的过程分析同插入结点一样,因此bistree_remove的时间复杂度为O(lg n)。
从AVL移除结点的过程分析同插入结点一样,因此,bistree_remove的时间复杂度为O(lgn)。
bistree_lookup
该操作用来在二叉搜索树中查找结点。返回一个指向AvlNode结构体中数据域成员的指针。该操作通过递归的方式调用lookup,从根结点开始,逐层降低遍历树的结点,直到找到目标结点为止。在每个层级上,我们首先检查是否到达了分支的边缘。如果我们处于分支的边缘就说明我们要找的结点不存在。否则,我们要么移动到左子结点,要么移动到右子结点,移动方式同前面介绍过的bistree_insert一样。当我们遇到目标结点时,递归终结,此时返回0。
查找Avl树中结点的分析过程同插入结点一样,因此bistree_lookup的时间复杂度为O(lg n)。
bistree_size
这是一个宏,用来计算二叉搜索树中结点的个数。直接访问BisTree结构体中的size成员即可。
示例:二叉搜索树抽象数据类型的实现(代码较长,请做好心理准备)
/*bistree.c*/ #include <stdlib.h> #include <string.h> #include "bistree.h" /*bistree.h中包含bitree.h*/ static void destroy_right(BisTree *tree,BiTreeNode *node); /* rotate_left 执行LL或LR旋转*/ static void rotate_left(BiTreeNode **node) { BiTreeNode *left, *grandchild; /*设left为A的左子树*/ left = bitree_left(*node); /*left结点的平衡因子为1,说明新插入的结点位于A的左子树的左子树上*/ if(((AvlNode *)bitree_data(left))->factor == AVL_LFT_HEAVY) { /*perform an LL rotation. 执行LL旋转*/ bitree_left(*node) = bitree_right(left); /*A的左指针指向left的右子结点*/ bitree_right(left) = *node; /*left的右指针指向A*/ ((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED; /*旋转后,将A的平衡因子改为0*/ ((AvlNode *)bitree_date(left))-factor = AVL_BALANCED; /*旋转后,将left的平衡因子改为0*/ *node = left; /*将原来指向A的指针指向left*/ } /*left结点的平衡因子不为1,说明插入的结点位于A的左子树的右子树上*/ else { /*perform an LR rotation. 执行LR旋转*/ grandchild = bitree_right(left); /*设grandchild为left的右子结点*/ bitree_right(left) = bitree_left(grandchild); /*将left的右子结点指向grch的左子结点*/ bitree_left(grandchild) = left; /*将grch的左子结点指向left*/ bitree_left(*node) = bitree_right(grandchild);/*将A的左子结点指向grch的右子结点*/ bitree_right(grandchild) = *node; /*grch的右子结点指向A*/ /*执行LR旋转后,调整结点的平衡因子取决于旋转前grch结点的原平衡因子值*/ switch(((AvlNode *)bitree_data(grandchild))->factor) { case AVL_LFT_HEAVY: /*如grch原平衡因子值为1,就将A的平衡因子设为-1,left的设为0*/ ((AvlNOde *)bitree_data(*node))->factor = AVL_RGT_HEAVY; ((AvlNode *)bitree_data(left))->factor = AVL_BALANCED; break; case AVL_BALANCED: /*如grch原平衡因子值为0,就将A的平衡因子设为0,left的设为0*/ ((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED; ((AvlNode *)bitree_data(left))->factor = AVL_BALANCED; break; case AVL_RGT_HEAVY: /*如grch原平衡因子值为-1,就将A的平衡因子设为0,left的设为1*/ ((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED; ((AvlNode *)bitree_data(left))->factor = AVL_LFT_HEAVY; break; } /*在所有情况下,grch的新平衡因子都为0*/ ((AvlNode *)bitree_data(grandchild))->factor = AVL_BALANCED; /*将原来指向A的指针指向grch.*/ *node = grandchild; } return; } /*rotate_right 执行LR旋转*/ static void rotate_right(BiTreeNode **node) { BiTreeNode *right, *grandchild; /*设right为A的右子树*/ right=bitree_right(*node); /*判断right的平衡因子,-1代表新节点位于A的右子树的右子树上*/ if(((AvlNode *)bitree_data(right))->factor == AVL_RGT_HEAVY) { /*perform an RR rotation. 执行RR旋转*/ bitree_right(*node)=bitree_left(right); /*将A的右子结点指向right的左子结点*/ bitree_right(right)=*node; /*将right的左子结点指向A*/ ((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED; /*将A的平衡因子设为0*/ ((AvlNode *)bitree_data(right))->factor = AVL_BALANCED; /*将right的平衡因子设为0*/ *node = right; /*原来指向A的指针指向right*/ } else { /*perform an RL rotation. 执行RL旋转*/ grandchild = bitree_left(right); /*设grch为right的左孩子*/ bitree_left(right) = bitree_right(grandchild); /*将right的左子结点指向grch的右子结点*/ bitree_right(grandchild) = right; /*将grch的右子结点指向right*/ bitree_right(*node)=bitree_left(grandchild); /*将A的右子结点指向grch的左子结点*/ bitree_left(grandchild) = *node; /*将grch的左子结点指向A*/ /*执行RL旋转后,调整结点的平衡因子取决于旋转前grch的原平衡因子*/ switch(((AvlNode *)bitree_data(grandchild))->factor) { case AVL_LFT_HEAVY:/*如grch原平衡因子值为1,就将A的平衡因子设为0,right的设为-1*/ ((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED; ((AvlNode *)bitree_data(*right))->factor = AVL_RGT_HEAVY; break; case AVL_BALANCED:/*如grch原平衡因子值为0,就将A的平衡因子设为0,right的设为0*/ ((AvlNode *)bitree_data(*node))->facotr = AVL_BALANCED; ((AvlNode *)bitree_data(right))->factor = AVL_BALANCED; break; case AVL_RGT_HEAVY:/*如grch原平衡因子值为-1,就将A的平衡因子设为1,right的设为0*/ ((AvlNode *)bitree_data(*node))->facotr = AVL_LFT_BALANCED; ((AvlNode *)bitree_data(right))->facotr = AVL_BALANCED; break; } /*在所有情况下,grch的新平衡因子都为0*/ ((AvlNode *)bitree_data(grandchild))->factor = AVL_BALANCED; /*将原来指向A的指针指向grch*/ *node = grandchild; } return; }
/*destroy_left 销毁左子树*/
static void destroy_left(BisTree *tree,BiTreeNode *node)
{
BiTreeNode **position;
/*如果树为空,直接返回*/
if(bitree_size(tree)==0)
return;
/*决定从何处销毁子树*/
if(node==NULL) /*node未指定,销毁整棵树*/
position = &tree->root;
else /*否则销毁指定结点的左子树*/
position = &node->left;
/*销毁子树*/
if(*position != NULL)
{
destroy_left(tree,*position); /*递归调用*/
destroy_right(tree,*position);
if(tree->destroy != NULL)
{
/*调用用户定义函数来释放动态分配的数据*/
tree->destroy(((AvlNode *)(*position)->data)->data);
}
/*释放AVL数据节点,并释放node结点本身*/
free((*position)->data);
free(*position);
*position = NULL;
/*调整树的大小*/
tree->size--;
}
return;
}
/*destroy_right 销毁右子树*/
static void destroy_right(BisTree *tree,BiTreeNode *node)
{
BiTreeNode **position;
/*如果树为空,直接返回*/
if(bitree_size(tree)==0)
return;
/*决定从何处销毁树*/
if(node==NULL) /*node未被指定时销毁整颗树*/
position=&tree->root;
else /*否则销毁指定结点的右子树*/
position=&node->right;
/*销毁子树*/
if(*position != NULL)
{
destroy_left(tree,*position);
destroy_right(tree,*position); /*递归调用*/
if(tree->destroy != NULL)
{
/*调用用户定义函数来释放动态分配的数据*/
tree->destroy(((AvlNode *)(*position)->data)->data);
}
/*释放AVL数据节点,并释放node结点本身*/
free((*position)->data);
free(*position);
/*重置*position*/
*position = NULL;
/*调整树的大小*/
tree->size--;
}
return;
}
/*insert 插入操作*/
static int insert(BisTree *tree,BiTreeNode **node,const void *data,int *balanced)
{
AvlNode *avl_data;
int cmpval,retval;
/*将数据插入到树中*/
/*如果*node是分支的结束,即*node=NULL*/
if(bitree_is_eob(*node))
{
/*操作插入到空树中,设置结点的AVL属性值*/
if((avl_data = (AvlNode *)malloc(sizeof(AvlNode)))==NULL)
return -1;
avl_data->factor = AVL_BALANCED;
avl_data->hidden = 0;
avl_data->data = (void *)data;
/*将数据插入为根结点*/
return bitree_ins_left(tree,*node,avl_data);
}
else
{
/*控制插入到非空树中 将待插入数据与当前结点的数据相比较*/
cmpval = tree->compare(data,((AvlNode *)bitree_data(*node))->data);
/*待插入结点的数据小于当前结点的数据*/
if(cmpval < 0)
{
/*向当前结点的左子树移动*/
/*如果当前结点的左子树不存在*/
if(bitree_is_eob(bitree_left(*node)))
{
if((avl_data = (AvlNode *)malloc(sizeof(AvlNode)))==NULL)
return -1;
/*将待插入结点插入到当前结点左侧,并设置AVL属性值*/
avl_data->factor=AVL_BALANCED;
avl_data->hidden=0;
avl_data->data=(void *)data;
if(bitree_ins_left(tree,*node,avl_data)!=0)
return -1;
*balanced=0;
}
/*如果当前结点的左子树不为空,递归调用insert向下插入*/
else
{
if((retval = insert(tree,&bitree_left(*node),data,balanced))!=0)
retrun retval;
}
}
/*确保树仍保持平衡*/
if(!(*balanced))
{
switch(((AvlNode *)bitree_data(*node))->factor)
{
case AVL_LFT_HEAVY:
rotate_left(node);
*balanced = 1;
break;
case AVL_BALANCED:
((AvlNode *)bitree_data(*node))->factor = AVL_LFT_HEAVY;
break;
case AVL_RGT_HEAVY:
((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED;
*balanced = 1;
break;
}
}
\*如果待插入结点的值大于当前结点的值*\
else if (cmpval>0)
{
/*向当前结点的右子树移动*/
/*如果当前结点的右子树不存在*/
if(bitree_is_eob(bitree_right(*node)))
{
if((avl_data = (AvlNode *)malloc(sizeof(AvlNode)))==NULL)
return -1;
/*将待插入结点插入到当前结点右侧,并设置AVL属性值*/
avl_data->factor = AVL_BALANCED;
avl_data->hidden = 0;
avl_data->data = (void *)data;
if(bitree_ins_right(tree,*node,avl_data)!=0)
return -1;
*balanced = 0;
}
/*如果当前结点的右子树不为空,递归调用insert向下插入*/
else
{
if(((retval = insert(tree,&bitree_right(*node),data,balanced))!=0)
return retval;
}
}
/*确定树仍然是保持平衡的*/
if(!(*balanced))
{
switch (((AvlNode *)bitree_data(*node))->factor)
{
case AVL_LFT_HEAVY:
((AvlNode *)bitree_data(*node))->factor = AVL_BALANCED;
*balanced = 1;
break;
case AVL_BALANCED:
((AvlNode*)bitree_data(*node))->factor = AVL_RGT_HEAVY;
break;
case AVL_RGT_HEAVY:
rotate_right(node);
*balanced=1;
}
}
}
/*待插入结点与当前结点(惰性隐藏)相等*/
else
{
if(!(AvlNode *)bitree_data(*node))->hidden)
{
return -1;
}
else
{
/*销毁当前结点中的数据*/
if(tree_destroy!=NULL)
{
tree->destroy(((AvlNode *)bitree_data(*node))->data);
}
/*将新数据插入到原来结点的位置上*/
((AvlNode *)bitree_data(*node))->data = (void *)data;
/*标识该结点不再为隐藏*/
((AvlNode *)bitree_data(*node))->hidden = 0;
/*这种情况下不需要再平衡树*/
*balanced = 1;
}
}
}
return 0;
}
/*hide 惰性移除*/
static int hide(BisTree *tree,BiTreeNode *node,const void *data)
{
int cmpval,retval;
if(bitree_is_eob(node))
{
/*数据没有被找到*/
return -1;
}
/*将待移除数据与当前结点数据相比较*/
cmpval = tree->compare(data,((AvlNode*)bitree_data(node))->data);
if(cmpval < 0)
{
/*向左移动*/
retval = hide(tree,bitree_left(node),data);
}
else if(cmpval > 0)
{
/*向右移动*/
retval = hide(tree,bitree_right(node),data);
}
else
{
/*两个数据相等,将结点隐藏*/
((AvlNode *)bitree_data(node))->hidden = 1;
retval = 0;
}
return retval;
}
/*lookup 查找二叉树中的结点*/
static int lookup(BisTree *tree,BiTreeNode *node,void **data)
{
int cmpval,retval;
if(bitree_is_eob(node))
{
/*数据结点没有找到*/
return -1;
}
cmpval = tree->compare(*data,((AvlNode *)bitree_data(node))->data);
if(cmpval < 0)
{
/*向左移动,递归查询*/
retval = lookup(tree,bitree_left(node),data);
}
else if(cmpval > 0)
{
/*向右移动,递归查询*/
retval = lookup(tree,bitree_right(node),data);
}
else
{
if(!(AvlNode *)bitree_data(node))->hidden)
{
/*找到结点且未被隐藏,从树中返回该结点数据*/
*data = ((AvlNode *)bitree_data(node))->data);
return 0;
}
else
{
/*如已隐藏,返回数据未被找到*/
return -1;
}
}
return retval;
}
/*bistree_init 初始化二叉搜索树*/
void bistree_init(BisTree *tree,int(*compare)(const void *key1,const void *key2),void (*destroy)(void *data))
{
bitree_init(tree,destroy);
tree->compare=compare;
return;
}
/*bistree_destroy 销毁二叉搜索树*/
void bistree_destroy(BisTree *tree)
{
/*Destroy all nodes in the tree.*/
destroy_left(tree,NULL);
/*No operations are allowed now,but clear the structure as a precaution.*/
memset(tree,0,sizeof(BisTree));
return;
}
/*bistree_insert 向二叉树中插入结点*/
int bistree_insert(BisTree *tree,const void *data)
{
int balanced=0;
return insert{tree,&bitree_root(tree),data,&balanced);
}
/*bistree_remove 惰性移除*/
int bistree_remove(BisTree *tree,const void *data)
{
return hide(tree,bitree_root(tree),data);
}



 浙公网安备 33010602011771号
浙公网安备 33010602011771号