集合实例（集合覆盖）

集合覆盖是一种优化求解问题，对很多组合数学和资源选择问题给出了很好的抽象模型。 问题如下：给定一个集合S，集合P由集合S的子集A1到An组成，集合C由集合P中的一个或多个子集组成。如果S中的每个成员都包含在C的至少一个子集中则称集合C覆盖集合S。此外，C包含的P的子集越少越好。

设想从一大群选手中挑选人员组建一支队伍，每名选手都拥有特定的技能组合。目标是组建出一只最小的队伍，使得队伍整体拥有一组特定的技能组合。也就是说，对于队伍整体所需要的技能，队伍中至少有一名选手必须拥有这项技能。假定S为队伍所必须拥有的技能集合，P为所有待选选手的技能集合。从P中挑选出一些技能组合以构成C，C必须覆盖S中所要求的所有技能。重要一点，我们选择的选手数量必须尽可能少。

针对集合覆盖的算法是一种近似算法，它并不总是获得最优解。该算法的工作原理是：

不断从P中选出一个集合，使其能够覆盖S中最多的成员数量。换句话说，该算法每次都尝试尽可能早覆盖S中更多的成员，因此该算法采用了贪心法的思路。由于每个集合都是从P中选出的，如果P被移除，则它的成员也将从S中移除。当P中剩余的成员没有任何集合能够覆盖S中的成员时，此时覆盖集合C就完成了。

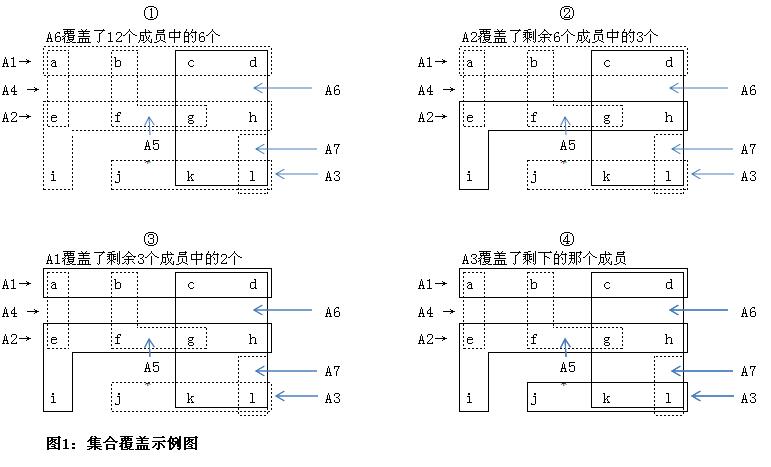
让我们看看对于12种技能的集合S={a,b,c,d,e,f,g,h,i,j,k,l}的最佳覆盖集。现在考虑有7名待选选手的集合P={A1,...A7}。P中选手拥有的技能集合为：A1={a,b,c,d}，A2={e,f,g,h}，A3={j,k,l}，A4={a,e}，A5={b,f,g}，A6={c,d,g,h,k,l}，A7={l}。最佳覆盖集应该是C={A1,A2,A3}。这里给出的算法选择的集合是C={A6,A2,A1,A3}（见图1）。

集合覆盖问题的函数实现

我们使用函数cover，该函数在集合P的子集A1~An中挑选出能够覆盖集合S的近似最优解。该函数有3个参数：

1、members是待覆盖的集合S；

2、subsets是集合P中的子集；

3、covering作为返回的覆盖集C。

该函数将修改所传入的3个参数，因此在调用该函数时，如果有必要话应该保存一份参数的拷贝。

函数执行过程：开始时，covering通过调用set_init先得到初始化。

我们使用循环进行迭代，只要members中还有未覆盖的成员，且subsets中的子集还没有挑选完，最外层的循环就得继续迭代。

在这个循环中，每次迭代时它都在subsets中找出能够覆盖到members的最大交集。

然后它将这个集合加到覆盖集covering中并把它的成员从members中移除（因为这些成员已经被覆盖，下一次迭代将判断剩余的成员能否被覆盖）。在循环的最后，将所选择的这个集合从subsets中移除（已经选中的要移除）。如果最外层的循环因为members不为空而终止迭代，则表示subsets中的集合不可能满足完全覆盖members的要求。同样，如果在迭代期间subsets中的成员无法与members的成员形成交集，则同样表示subsets中的成员无法满足完全覆盖members的要求。函数cover如果找到了一个完全覆盖解，该函数返回0，参数covering指向这个完全覆盖解；如果不可能实现完全覆盖，则返回1；其他情况返回-1。

cover的复杂度为O(m³)，这里的m代表members集合中的初始成员个数。在最坏的情况下，对于members中的每一员，subsets中都只有唯一一个子集与之对应，此时的复杂度是O(m_³)。在这种情况下，subsets有 m个子集，set_intesection以O(m)的复杂度执行，因为当计算和members求交集时，subsets的每个子集都只有唯一一个个成员需要遍历。因此cover的内层循环是O(m²)的，而这个循环要执行m次。

示例1：集合覆盖问题的头文件

#ifndef COVER_H
#define COVER_H

#include "set.h"

typedef struct KSet_
{
    void *key;
    Set set;
}KSet;

int cover(Set *member, Set *subsets, Set *covering);

#endif 

 示例2：集合覆盖问题的函数实现

#include <stdlib.h>
#include "cover.h"
#include "list.h"
#include "set.h"

int cover(Set *members, Set *subsets, Set *covering)
{
    Set intersection;
    KSet *subset;
    ListElmt *member,*max_member;
    void *data;
    int max_size;
    
    /*初始化覆盖集covering*/
    set_init(covering,subsets->match,NULL);
    
    while(set_size(members)>0 && set_size(subsets)>0)
    {
        /*找到能够覆盖最多members成员的子集*/
        max_size = 0;
        for(member = list_head(subsets);member!=NULL;member=list_next(member))
        {
            if(set_intersection(&intersection, &((KSet *)list_data(member))->set, members) != 0)
                return -1;
            
            if(set_size(&intersection)>max_size)
            {
                max_member = member;
                max_size = set_size(&intersection);
            }
            
            set_destroy(&intersection);
        }
        /*如果不存在交集，那么就不可能有覆盖集*/
        if(max_size==0)
            return 1;
        
        /*将被选到的子集插入覆盖集covering中*/
        subset = (KSet *)list_data(max_member);
        
        if(set_insert(covering,subset) != 0)
            return -1;
        
        /*从members中移除已经被覆盖的元素*/
        for(member=list_head(&((Kset *)list_data(max_member))->set);member != NULL;
            list_next(member))
        {
            data = list_data(member);
            if(set_remove(members,(void **)data)== 0 && members->destroy != NULL)
                members->destroy(data);
        }
        
        /*从子集集合中删除已经被选用的子集*/
        if(set_remove(subsets,(void **)&subset) != 0)
            return -1;
    }
    
    /*如果members中仍然存在未被覆盖的元素，那么也不可能实现完全覆盖*/
    if(set_size(members)>0)
        return -1;
    
    return 0;
}