将递归函数非递归化的一般方法
在C语言编程中,使用递归函数实现一个特定的功能,好处是代码简洁,坏处是可读性可能不是很好(甚至可读性很差)。另外,栈的长度是有限的,如果使用递归,很明显地加重了栈的负担。
例如: (下面的函数实现了一个非常简单的功能: 判定输入的整数是否是2的N次方,N=0,1,2...)
1 bool isPowerOfTwo(int n) { 2 if (n <= 0) 3 return false; 4 if (n == 1) 5 return true; 6 if (n % 2 == 0) { 7 return isPowerOfTwo(n/2); 8 } 9 return false; 10 }
代码实现确实简洁,可读性也挺好。但是对栈(Stack)使用得比较狠,看下面的反汇编代码,
1 (gdb) set disassembly-flavor intel 2 (gdb) disas /m isPowerOfTwo 3 Dump of assembler code for function isPowerOfTwo: 4 6 bool isPowerOfTwo(int n) { 5 0x0804844d <+0>: push ebp 6 0x0804844e <+1>: mov ebp,esp 7 0x08048450 <+3>: sub esp,0x18 8 9 7 if (n <= 0) 10 0x08048453 <+6>: cmp DWORD PTR [ebp+0x8],0x0 11 0x08048457 <+10>: jg 0x8048460 <isPowerOfTwo+19> 12 13 8 return false; 14 0x08048459 <+12>: mov eax,0x0 15 0x0804845e <+17>: jmp 0x8048492 <isPowerOfTwo+69> 16 17 9 if (n == 1) 18 0x08048460 <+19>: cmp DWORD PTR [ebp+0x8],0x1 19 0x08048464 <+23>: jne 0x804846d <isPowerOfTwo+32> 20 21 10 return true; 22 0x08048466 <+25>: mov eax,0x1 23 0x0804846b <+30>: jmp 0x8048492 <isPowerOfTwo+69> 24 25 11 if (n % 2 == 0) { 26 0x0804846d <+32>: mov eax,DWORD PTR [ebp+0x8] 27 0x08048470 <+35>: and eax,0x1 28 0x08048473 <+38>: test eax,eax 29 0x08048475 <+40>: jne 0x804848d <isPowerOfTwo+64> 30 31 12 return isPowerOfTwo(n/2); 32 0x08048477 <+42>: mov eax,DWORD PTR [ebp+0x8] 33 0x0804847a <+45>: mov edx,eax 34 0x0804847c <+47>: shr edx,0x1f 35 0x0804847f <+50>: add eax,edx 36 0x08048481 <+52>: sar eax,1 37 0x08048483 <+54>: mov DWORD PTR [esp],eax 38 0x08048486 <+57>: call 0x804844d <isPowerOfTwo> 39 0x0804848b <+62>: jmp 0x8048492 <isPowerOfTwo+69> 40 41 13 } 42 14 return false; 43 0x0804848d <+64>: mov eax,0x0 44 45 15 } 46 0x08048492 <+69>: leave 47 0x08048493 <+70>: ret 48 49 End of assembler dump. 50 (gdb)
4 6 bool isPowerOfTwo(int n) {
5 0x0804844d <+0>: push ebp
6 0x0804844e <+1>: mov ebp,esp
7 0x08048450 <+3>: sub esp,0x18
..
38 0x08048486 <+57>: call 0x804844d <isPowerOfTwo>
..
由此可见,每一次call, L5,L7和L38都会对栈指针寄存器(esp)进行修改,
L38: 将eip压入stack中, (esp减小4字节)
L5: 将ebp压入stack中, (esp减小4字节)
L7: 将esp减小0x18 (即esp减小24字节)
也就是说,每一次call, esp减小(至少)32个字节。 如果n = 2^32, 那么esp减小约32 * 32 = 1024字节 = 1KB.
为了尽可能地减少使用栈的次数(注:请"惜栈如金",本质上是"惜内存",随意浪费内存的程序员不是好程序员!),有必要对递归函数非递归化。
下面给出去递归化的一般方法。
第1步,使用goto语句对递归函数进行改造。因为在汇编里,没有if..else../while/for之类的flow control语句,只有cmp+jmp。
改造后的代码如下:
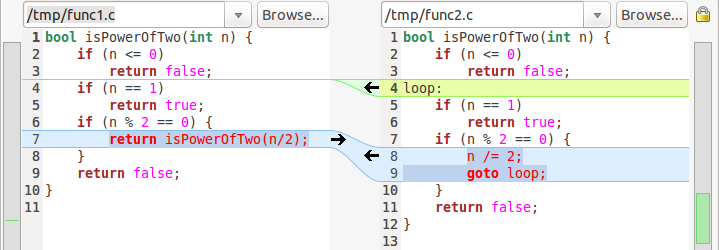
1 bool isPowerOfTwo(int n) { 2 if (n <= 0) 3 return false; 4 loop: 5 if (n == 1) 6 return true; 7 if (n % 2 == 0) { 8 n /= 2; 9 goto loop; 10 } 11 return false; 12 }
用meld对比一下(帮助理解), 【注:meld是使用Python实现的一个超好用的diff和merge代码的工具】
第2步,将使用goto语句改造的结果用while/for做进一步改造。因为在C语言编程中goto语句不被推荐(但是:goto语句不是不可以用而是不要滥用,完全放弃使用goto语句也是不合适的, 因为使用goto做cleanup还是很棒的,不信你去看看操作系统内核的源代码)。
改造后的代码如下:
1 bool isPowerOfTwo(int n) { 2 if (n <= 0) 3 return false; 4 while (n >= 1) { 5 if (n == 1) 6 return true; 7 if (n % 2 == 0) { 8 n /= 2; 9 } else { 10 break; 11 } 12 } 13 return false; 14 }
再次用meld对比一下,
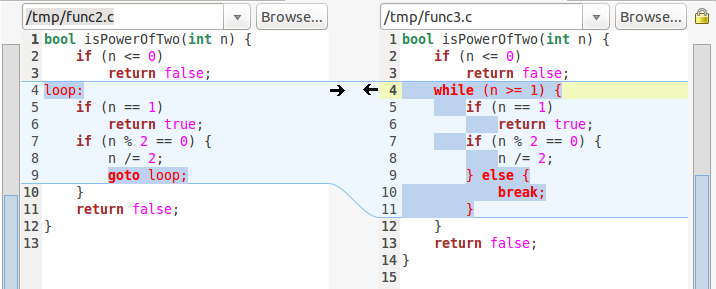
对汇编感兴趣的朋友可以将上图中的函数反汇编后diff它们之间的差异,应该差异不大。
总结: 将递归函数非递归化,一般分两步。
第1步,使用goto语句对递归函数进行改造;
第2步,将使用goto语句改造的结果用while/for做进一步改造。
透过方法看本质,此方法实质上是从汇编的视角看C递归函数,然后本着能不给栈(stack)添堵就不给栈添堵的原则,尽可能地减少函数调用从而达到去递归化的目的。
扩展问题: 如果一个递归函数无法直接用while/for改造怎么办? (比如二叉搜索树的遍历)
1 typedef struct bst_node_s { 2 int key; 3 struct bst_node_s *left; 4 struct bst_node_s *right; 5 } bst_node_t; 6 7 void 8 bst_walk(bst_node_t *root) /* Walk by InOrder */ 9 { 10 if (root == NULL) 11 return; 12 bst_walk(root->left); 13 printf("%d\n", root->key); 14 bst_walk(root->right); 15 }
解决方案: 用C构建一个自己的栈(数据类型),然后使用push(), pop()函数改造从而实现去递归化。



