从整数裂项说开去

1. 整数裂项概述

1.1 1 * 2 + 2 * 3 + 3 * 4 + ... + (n - 1) * n = ?

解:  裂项公式为：

 (n - 1) * n = [(n - 1) * n * (n + 1) - (n - 2) * (n - 1) * n] / 3

求解过程如下图所示：

 

1.2 1 * 2 * 3 + 2 * 3 * 4 + 3 * 4 * 5 + ... + (n - 2) * (n - 1) * n = ?

解:  裂项公式为：

 (n - 2) * (n - 1) * n = [(n - 2) * (n - 1) * n * (n + 2) - (n - 3) * (n - 2) * (n - 1) * n] / 4

求解过程如下图所示：

 

1.3 1 * 3 + 3 * 5 + 5 * 7 + ... + 19 * 21 = ?

解:  注意在每个加数的两个因数中，公差为2。求解过程如下图所示：

 

1.4 5 * 10 * 15 + 10 * 15  * 20 +  ... + 40 * 45 *50 = ?

解:  注意在每个加数的三个因数中，公差为5。求解过程如下图所示：

 

 

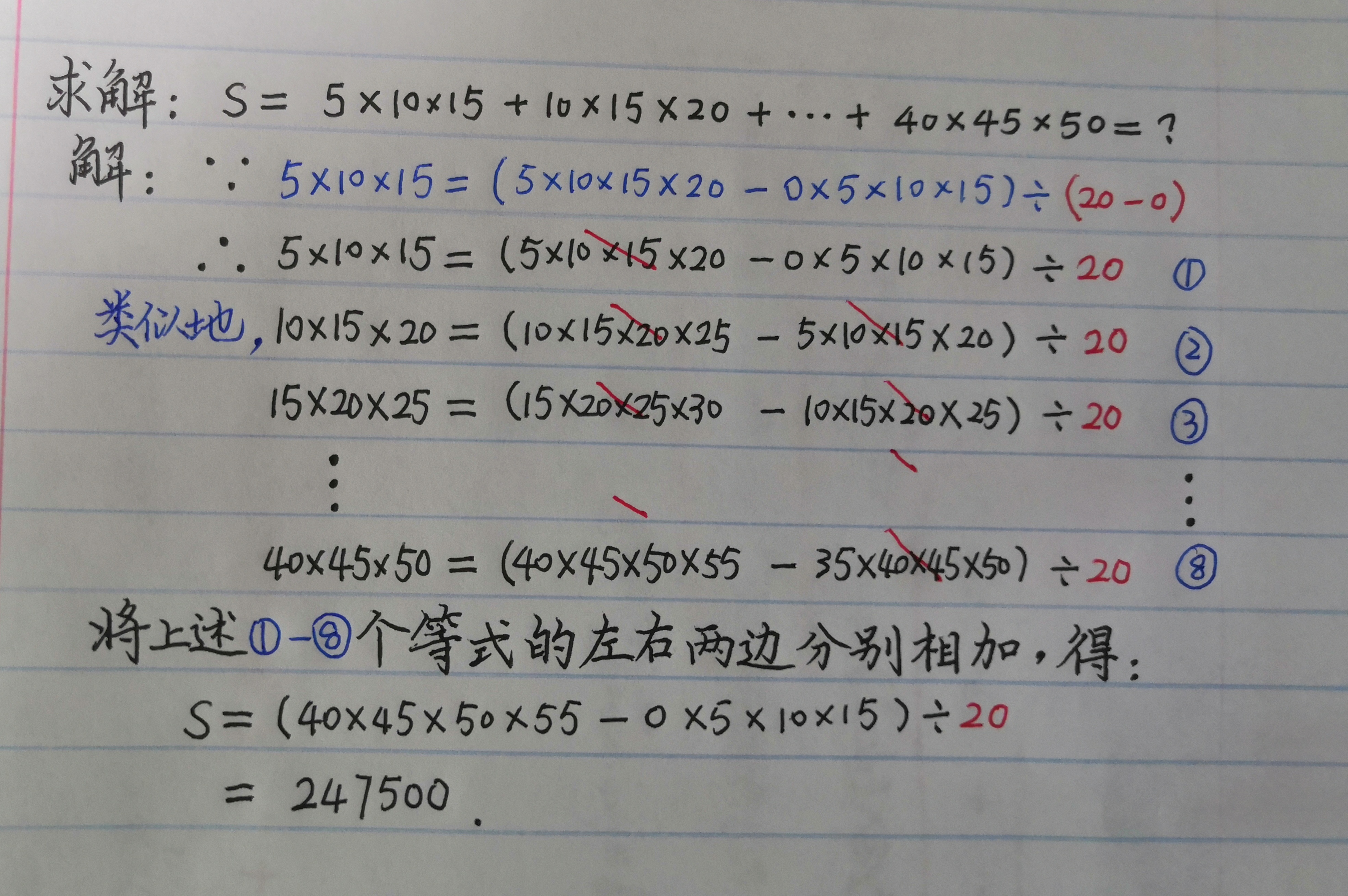
2. 关于1**2 + 2**2 + 3**2  + ... + n**2 = n * (n + 1) * (2n +1） /  6的证明

证明的要点为：

n ** 2 = n ** 2 - 1 + 1
       = n ** 2 - 1 ** 2 + 1
       = (n - 1) * (n + 1) + 1

证明过程如下图所示：

 

 

3. 关于1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 + ... + 97 * 98 * 99 * 100 = ?的求解

这类问题的求解比前面的问题要复杂得多，因为两个相邻加数中，因数不满足可直接裂项的连续性，即：

1 * 2 * 3  * 4 + 2 * 3 * 4  * 5 

是满足可直接裂项的连续性的，但是

1 * 2 * 3 * 4 + 3 * 4 * 5 * 6

并不满足可直接裂项的连续性。怎么办？

典型思路就是：构造满足可直接裂项的连续性的序列，然后通过解方程组间接求解。

在未求解之前，我们先用一个很硬核的求解程序（暴力累加），看看结果是什么。

3.1 硬核求解程序

• foo.py （算法简单粗暴）

#!/usr/bin/python3
""" Question:
1 * 2 * 3 * 4 +
        3 * 4 * 5 * 6 +
                5 * 6 * 7 * 8 +
                        ...   +
                        97 * 98 * 99 * 100
=
        4!     6!     8!           100!
       ---- + ---- + ---- + ... + -----
        0!     2!     4!            96!
= ?
"""
import sys


def main(argc, argv):
    if argc < 2:
        print("Usage: %s <N> [-D]" % argv[0], file=sys.stderr)
        print("e.g.", file=sys.stderr)
        print("       %s 96" % argv[0], file=sys.stderr)
        print("       %s 96 -D" % argv[0], file=sys.stderr)
        return 1

    n = int(argv[1])
    if argc == 3 and argv[2] == '-D':
        debug = True
    else:
        debug = False

    a = []
    i = 0
    s = 0
    while i <= n:
        x = (i + 1) * (i + 2) * (i + 3) * (i + 4)
        a.append('%d * %d * %d * %d' % (i + 1, i + 2, i + 3, i + 4))
        s += x
        i += 2
    if debug:
        print('%s = %d' % (' + '.join(a), s))
    else:
        b = [a[0], a[1], a[2], '...', a[-1]]
        print('%s = %d' % (' + '.join(b), s))

    return 0


if __name__ == '__main__':
    sys.exit(main(len(sys.argv), sys.argv))

• 运行foo.py

huanli@idorax16:~$ ./foo.py 96 -D
1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 + 7 * 8 * 9 * 10 + 9 * 10 * 11 * 12 + 11 * 12 * 13 * 14 + 13 * 14 * 15 * 16 + 15 * 16 * 17 * 18 + 17 * 18 * 19 * 20 + 19 * 20 * 21 * 22 + 21 * 22 * 23 * 24 + 23 * 24 * 25 * 26 + 25 * 26 * 27 * 28 + 27 * 28 * 29 * 30 + 29 * 30 * 31 * 32 + 31 * 32 * 33 * 34 + 33 * 34 * 35 * 36 + 35 * 36 * 37 * 38 + 37 * 38 * 39 * 40 + 39 * 40 * 41 * 42 + 41 * 42 * 43 * 44 + 43 * 44 * 45 * 46 + 45 * 46 * 47 * 48 + 47 * 48 * 49 * 50 + 49 * 50 * 51 * 52 + 51 * 52 * 53 * 54 + 53 * 54 * 55 * 56 + 55 * 56 * 57 * 58 + 57 * 58 * 59 * 60 + 59 * 60 * 61 * 62 + 61 * 62 * 63 * 64 + 63 * 64 * 65 * 66 + 65 * 66 * 67 * 68 + 67 * 68 * 69 * 70 + 69 * 70 * 71 * 72 + 71 * 72 * 73 * 74 + 73 * 74 * 75 * 76 + 75 * 76 * 77 * 78 + 77 * 78 * 79 * 80 + 79 * 80 * 81 * 82 + 81 * 82 * 83 * 84 + 83 * 84 * 85 * 86 + 85 * 86 * 87 * 88 + 87 * 88 * 89 * 90 + 89 * 90 * 91 * 92 + 91 * 92 * 93 * 94 + 93 * 94 * 95 * 96 + 95 * 96 * 97 * 98 + 97 * 98 * 99 * 100 = 974510040

huanli@idorax16:~$ ./foo.py 96 
1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8 + ... + 97 * 98 * 99 * 100 = 974510040

 

在正式求解此问题之前，先来个简单一点的问题。例如：

1 * 2 + 3 * 4 + 5 * 6 + ... + 99 * 100 = ? 

 

3.2 关于1 * 2 + 3 * 4 + 5 * 6 + ... + 99 * 100 = ?的求解

• 用Python代码求解结果如下：

>>> s = 0
>>> i = 1
>>> while i <= 99:
...    x = i * (i + 1)
...    s += x
...    i += 2
... 
>>> s
169150

• 基于整数裂项+构造方程组的求解过程如下：

 

3.3 关于1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6  * 7 * 8 + ... + 97 * 98 * 99 * 100 = ?的求解

本题为小学六年级奥数题，题目难度比较大，至少对小学六年级学生来说很有挑战性。有了3.2的基础，接下来的求解思路就很清楚了，只是求解过程需要逐次降阶而已。

求解过程如下所示：

 

在上述求解过程中，一共使用了整数裂项3次，解二元一次方程组3次。因为既包括整数裂项、等差数列求和和解方程组，故难度较大。

那么，如果做如下推广，将如何？

a) 1 * 2 * 3 * 4 + 3 * 4 * 5 * 6 + 5 * 6 * 7 * 8    + ... + (2m-1)*(2m)*(2m+1)*(2m+2) = ?
b) 1 * 2 * 3 * 4 + 5 * 6 * 7 * 8 + 9 * 10 * 11 * 12 + ... + (4m+1)*(4m+2)*(4m+3)*(4m+4) = ? 

4. 结束语

裂项求和是分解与组合思想在数列求和中的具体应用。其中，整数裂项求和，可直接解决诸如：

1 * 2 + 2 * 3 + 3 * 4 + ... + (n-1) * n = ?
1 * 2 * 3 + 2 * 3 * 4 + 3 * 4 * 5 + ... + (n-2) * (n-1) * n = ?

之类的问题，但无法直接解决

1 * 2 + 3 * 4 + 5 * 6 + ... + (2m - 1) * 2m = ?

之类的问题。后者之所以不能被直接解决，是因为不满足可整数裂项的连续性。对这类问题的求解，不但借助了解方程组的思想，而且利用了逐级降阶的方法，实为有趣。

更一般地，下面的问题可递归求解。

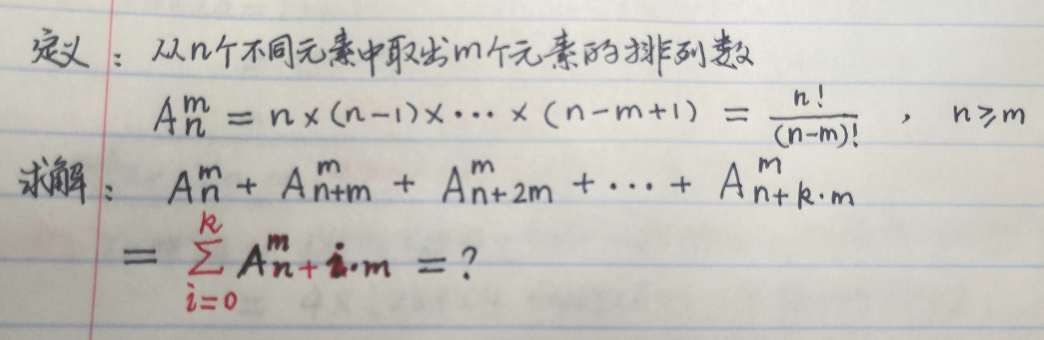
例如：

# n = m = 10, k = 9

   1 *  2 *  3 *  4 *  5 *  6 *  7 *  8 *  9 * 10 
+ 11 * 12 * 13 * 14 * 15 * 16 * 17 * 18 * 19 * 20
+ 21 * 22 * 23 * 24 * 25 * 26 * 27 * 28 * 29 * 30
+ ...
+ 91 * 92 * 93 * 94 * 95 * 96 * 97 * 98 * 99 * 100 
= ?

 

参考资料：

1. 整数裂项公式推导