区间更新、求和问题

树状数组、线段树的实现与应用、模运算的使用。

一、题目

  定义在数组上的操作，给定大小为N的数组以及N个数。之后给出M个操作，则要输入M行。每一行操作第一个数代表操作类型，要么是U要么是C。对于U类型的操作，紧跟3个数a、b、k，也就是把数组下标a到b的每个数替换为该数的k次方(防止数过大，因此对1234567891取模)。而对于C操作，则紧跟a、b两个数，表示输出数组下标a到b的所有数和。

  可以发现，题目描述的是典型的区间更新和查询的问题。因此对于区间问题同时考虑到效率，可以使用树状数组或者线段树进行问题的求解。同时取模操作的话也可以选择恰当的方法进行优化。

二、树状数组

树状数组:树状数组就是用数组来模拟树形结构，可以说树状数组能解决的问题线段树都可以解决。但是树状数组的系数少，且不需要建树。因此使用、实现更加简单。

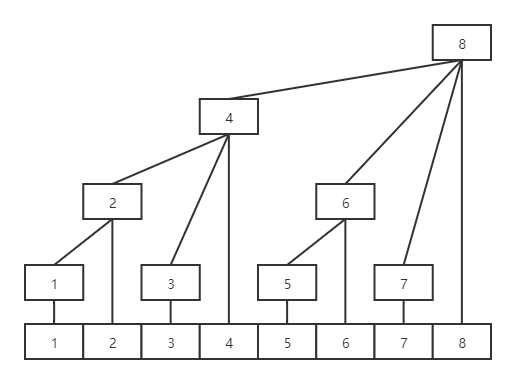
  树状数组的修改和查询的复杂度都是O(logN)，但是其功能有限，适合解答简单的区间问题。树状数组的原理就是额外定义一个和原数组A一样大小的数组C。同时规定C[i]=A[i-2^k+1]+A[i-2^k+2]+A[i]，其中k规定为i的二进制中低位至高位连续0的长度。那么2^k就是i的第一位非0位大小，同时根据位运算，可以得到2^k=i&(-i)，且这种运算叫做lowbit(如当i=2时,lowbit(2)=2,此时C[2]=A[2-2+1]+A[2]=A[1]+A[2])。

单点修改、区间查询:
  定义了树状数组后，可以很方便的求得任意项前缀和sum_i=c[i]+c[i-2^k1]+c[(i-2^k1)-2^k2]+...(如当i=7,有sum₇=C[7]+C[7-lowbit(7)]+C[6-lowbit(6)]=C[7]+C[6]+C[4])。不难发现对于每个C[i]其就是数组(i-lowbit(i),i]的区间和。所以sum_i就是求出这几个连续区间的和，如sum₇就是求解[1,4]、[5,6],[7,7]的和。

  更新时只要更新了某个值，更新该值所影响的数组C的值就可以实现全局的更新。对于更新了A[i],可以假设C[j]可以覆盖A[i],且lowbit(j)=2^k。所以对于j满足其前k-1位为0,第k位为1,剩余位需和i一样(满足条件j-lowbit(j)<i)。当2^k<lowbit(i),此时j<i肯定不满足。当2^k=lowbit(i),此时j=i，肯定满足。而当2^k>lowbit(i)时，此时j-lowbit(j)<i是满足的，所以可以覆盖到i。而满足的最小j就是i+lowbit(i),且可以发现树状数组中覆盖是向上传递的，因此每次得到j当做新的i处理就可以更新全部的C数组值。

区间修改、单点查询:
  为了实现区间修改，需要额外引入差分数组D,对于原数组A有D[i]=A[i]-A[i-1]。因此可以在D数组上建立树状数组,其前缀和sum_di=D[1]+D[2]+..D[i],可以发现sum_di=A[i]。因此单点查询只要求出D[i]树状数组的前缀和就可以得到结果。

  而对于区间修改，比如将A数组区间[l,r]的所有数加val。那么对于对于D数组,其实改变的差分只有D[l]和D[r+1]的值，因此就将区间修改转换为单点修改的问题，由此简化了区间修改问题。

区间修改、区间查询:
  该问题同样需要引入差分的概念,对于数组A,其前缀和sum_ai=A[1]+A[2]+...+A[i]=D[1]+D[1]+D[2]+...+D[1]+D[2]+...+D[i]。所以sum_ai=∑ⁱ_j=1D[j](i-j+1)=(i+1)∑ⁱ_j=1D[j]-∑ⁱ_j=1D[j]j。因此本问题还需要额外维护一个数组D'[i]=D[i]i。所以查询位置i前缀和就是(i+1)*D数组中i的前缀和-D'数组中i的前缀和。区间查询就是两个前缀和相减。

  区间修改时数组D的做法依旧，对于数组D'更新如将区间[l,r]加val，则对于D[l]位置是加lval,对于D[r+1]位置则是减(r+1)val。

import java.util.Scanner;
public class Main {
    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt();
        int m = scanner.nextInt();
        BITree biTree = new BITree(n);
        for (int i = 1; i <= n; i ++) {
            biTree.A[i] = scanner.nextInt();
            biTree.update(i, biTree.A[i]);
        }
        for (int i = 0; i < m; i ++) {
            String op = scanner.next();
            int a = scanner.nextInt();
            int b = scanner.nextInt();
            if ("U".equals(op)) {
                int k = scanner.nextInt();
                update(biTree, a, b, k);
            } else {
                System.out.println(count(biTree, a, b));
            }
        }
    }

    public static void update(BITree biTree, int a, int b, int k) {
        for (int i = a; i <= b; i ++) {
            int temp = biTree.A[i];
            biTree.A[i] = (int) Math.pow(temp, k);
            biTree.update(i, biTree.A[i] - temp);
        }
    }

    public static int count(BITree biTree, int a, int b) {
        return biTree.getSum(b) - biTree.getSum(a - 1);
    }
}

class BITree {
    public int[] A, C;
    public BITree(int n) {
        A = new int[n + 1];
        C = new int[n + 1];
    }

    public void update(int i, int k) {
        if (i >= C.length) return;
        C[i] = C[i] + k;
        update(i + lowbit(i), k);
    }

    public int getSum(int i) {
        if (i <= 0) return 0;
        return C[i] + getSum( i - lowbit(i));
    }

    private int lowbit(int i) {
        return i & (-i);
    }
}

三、线段树

线段树:线段树是一种二叉搜索树，与区间树相似，它将一个区间划分成一些单元区间，每个单元区间对应线段树中的一个叶结点。每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。因此线段树是平衡二叉树，最后的子节点数目为N，即整个线段区间的长度。

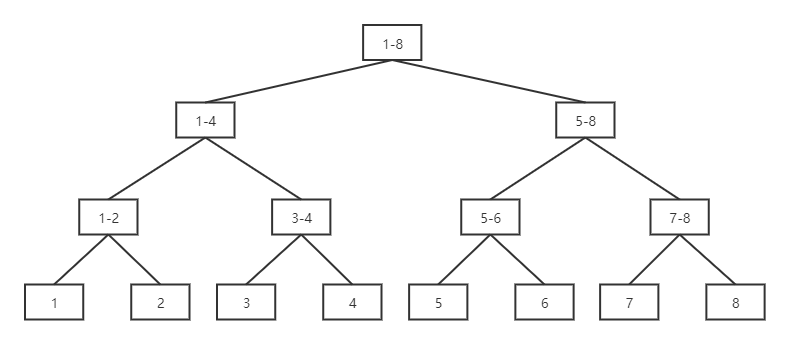
  线段树的原理就是将[1,n]分解成若干特定的子区间(数量不超过4n),将每个区间[L,R]都分解为少量特定的子区间，通过对这些少量子区间的修改或者统计，来实现快速对[L,R]的修改或者统计。从图中可以发现，每个区间都是一个节点，每个节点存自己对应的区间的统计信息。所以线段树统计的东西，必须符合区间加法。其存储结构多采用数组实现，且对于节点R，左子节点为2R,右子节点为2*R+1。所需的数组元素个数为2^log₂n+1,多开四倍空间。

单点修改:
  可以发现对于最底层的每个节点，之上没一层只有一个区间结点包含该结点的值。因此单点修改时，只需要修改每一层包含该结点的区间即可。而线段树是平衡二叉树，树高为logN(大致的证明就是求解递归方程)。所以修改的时间复杂度为O(logN)。

区间查询:
  证明线段树能进行快速的区间查询使用定理:n>=3时,一个[1,n]的线段树可以将[1,n]的任意子区间[L,R]分解为不超过2⌊log₂(n-1)⌋个子区间。因此查询区间[L,R]的统计信息,访问的结点不会超过2⌊log₂(n-1)⌋个，实现O(logN)的时间复杂度的区间查询。定理大致的理解就是从底层往上层分析,对于底层结点，两两结点往上层合并，因此对于区间[L,R],除了L、R边界结点刚好是两两结点中的一个，其余结点都是可直接查询它们父结点代替的。因此最底层至多查询两个结点。由此可得出每一层最多查询两个结点，那么大致查询的节点个数为2倍树高。而完整的证明则可以使用数学归纳法。

区间修改:
  线段树的区间修改也是将区间分成子区间，同时为了提高效率，加入了懒惰标记。懒惰标记的大致作用表示更新了区间的统计信息，但是其子节点还未进行更新。这样子提高了区间修改的效率，保证区间修改也可以在O(logN)时间复杂度内完成。

  实际懒惰标记分为相对标记和绝对标记。相对标记的标记直接可以共存(如将区间的所有数+a),和打标记的顺序无关。所有可以在区间修改时不下推标记，而在区间查询时下推标记。绝对标记打标记的顺序会影响结果(如将区间所有数变为a),因此这种标记区间修改时必须要下推旧的标记。另外非递归线段树只能维护相对标记，因为其是自底向上直接修改分成的每个子区间，所以根本做不到在区间修改的时候下推标记。且一般不下推标记，而是自下而上求答案的过程中，根据标记更新答案。

import java.util.Scanner;
public class Main {

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(), m = scanner.nextInt();
        int[] nums = new int[n + 1];
        for (int i = 1; i <= n; i ++) nums[i] = scanner.nextInt();
        SegTree segTree = new SegTree(n, nums);
        for (int i = 0; i < m; i ++) {
            String op = scanner.next();
            int L = scanner.nextInt();
            int R = scanner.nextInt();
            if ("U".equals(op)) {
                int c = scanner.nextInt();
                segTree.rangeUpdate(L, R, c, 1, n, 1);
            } else {
                System.out.println(segTree.rangeQuery(L, R, 1, n, 1));
            }
        }
    }

}

class SegTree {
    private Node[] nodes;
    private int[] nums;

    private class Node {
        int l, r;
        int val, lazy;
        Node(int l, int r) {
            this.l = l;
            this.r = r;
            this.val = this.lazy = 0;
        }
    }

    public SegTree(int n, int[] nums) {
        nodes = new Node[4 * n];
        this.nums = nums;
        build(1, n, 1);
    }

    /**
     * @description 单点更新，更新路径上所有结点。
     */
    public void update(int L, int c, int l, int r, int rt) {
        if (l == r) {
            nodes[rt].val += c;
            return;
        }
        int m = (l + r) >> 1;
        if (L <= m) update(L, c, l, m, rt << 1);
        else update(L, c, m + 1, r, rt << 1 | 1);
        pushUp(rt);
    }

    /**
     * @description 区间更新,只要区间结点在指定范围内，那么就可直接更新同时
     * 做懒标记处理。否则就要对其两个子节点进行搜索，这一步需提前下推旧的懒标
     * 记。递归搜索直到结束即可。
     */
    public void rangeUpdate(int L, int R, int c, int l, int r, int rt) {
        if (L <= l && r <= R) {
            nodes[rt].val += c * (r - l + 1);
            if (l != r) nodes[rt].lazy += c;
            return;
        }
        int m = (l + r) >> 1;
        pushDown(rt, m - l + 1, r - m);
        if (L <= m) rangeUpdate(L, R, c, l, m, rt << 1);
        if (R > m) rangeUpdate(L, R, c, m + 1, r, rt << 1 | 1);
        pushUp(rt);

    }

    /**
     * @description 区间查询，区间节点在指定范围内直接返回结果。否则要进行
     * 左右节点的递归搜索，搜索之前提前下推懒标志。最后所以结果累加返回。
     */
    public int rangeQuery(int L, int R, int l, int r, int rt) {
        if (L <= l && r <= R) return nodes[rt].val;
        int m = (l + r) >> 1, res = 0;
        pushDown(rt, m - l + 1, r - m);
        if (L <= m) res += rangeQuery(L, R, l, m, rt << 1);
        if (R > m) res += rangeQuery(L, R, m + 1, r, rt << 1 | 1);
        return res;
    }

    /**
     * @description 建树操作，递归结束就是l=r，到达叶子结点，否则不断二分。
     */
    private void build(int l, int r, int rt) {
        nodes[rt] = new Node(l, r);
        if (l == r) {
            nodes[rt].val = nums[l];
            return;
        }
        int m = (l + r) >> 1;
        build(l, m, rt << 1);
        build(m + 1, r, rt << 1 | 1);
        pushUp(rt);
    }

    /**
     * @description 递归返回时更新上层节点的值为其子节点和。
     */
    private void pushUp(int rt) {
        nodes[rt].val = nodes[rt << 1].val + nodes[rt << 1 | 1].val;
    }

    /**
     * @description 懒标记下推函数，每一次操作只下推一层，更新了左右节点的值和懒
     * 标记，并清除自身的懒标记。
     */
    private void pushDown(int rt, int ln, int rn) {
        if (nodes[rt].lazy != 0) {
            nodes[rt << 1].lazy = nodes[rt].lazy;
            nodes[rt << 1 | 1].lazy = nodes[rt].lazy;
            nodes[rt << 1].val += nodes[rt].lazy * ln;
            nodes[rt << 1 | 1].val += nodes[rt].lazy * rn;
            nodes[rt].lazy = 0;
        }
    }

}

四、模运算

模运算:指取模运算，用符号%表示。m%n即求m/n的余数。

负数模运算:
  模运算和整数除法运算是相关的，而整数除法运算考虑到取整问题又分为向上取整、向下取整、向零取整。

 向上取整:取比实际结果稍大的最小整数，也叫做Ceiling取整。此时有17/10=2、5/2=3、-9/4=-2。
 向下取整:取比实际结果稍小的最大整数，也叫Floor取整。此时有17/10=1、5/2=2、-9/4=-3。
 向零取整:向0方向取最接近精确值的整数，换言之就是舍去小数部分，因此又称截断取整（Truncate）。此时17/10=1、5/2=2、-9/4=-2。

  因此在知道整除结果的情况，模就是两数相除以后的余数。假设q是a、b相除产生的商，r是余数。那么满足a=b×q+r,其中|r|<|a|。因此r可整可负，相应的q也有两个选择。但一般当a、b为正，r取整。a、b都为负，r取负数。而当a、b一正一负，不同的语言所带来的结果可能不一样，但r计算方法满足r=a-(a/b)×b。

C\Java等大多数语言都采用truncate除法，所以有:
  -17 % 10:r = (-17) - (-17 / 10) × 10 = (-17)-(-1 × 10) = -7
  17 % -10:r = (17) - (17 / (-10)) × (-10) = 17 - (-1) × (-10) = 17 - 10 = 7
  -17 % -10:r = (-17) - (-17 / (-10)) × (-10) = (-17) - 1 × (-10) = -7
对于Python语言，除法采用的则是floor除法，有:
  -17 % 10:r = (-17) - (-17 / 10) × 10 = (-17)-(-2 × 10) = 3
  17 % -10:r = (17) - (17 / (-10)) × (-10) = 17 - (-2) × (-10) = 17 - 20 = -3
  -17 % -10:r = (-17) - (-17 / (-10)) × (-10) = (-17) - 1 × (-10) = -7

快速幂模算法:
  在计算乘法运算时，暴力的解法就是对于每个底数，相乘指数次，因此引入快速乘方运算。计算a^b时，当b是奇数时,a^b=a×(a²)^(b-1)/2,偶数时有a^b=(a²)^(b)/2,那么每次只需要乘自身，指数减一半。因此时间复杂度可以降至O(logN)。还有一种就是指数转为二进制的形式，每次需要维护相应位数的乘法值，时间复杂度也是O(logN)。

//方法1
public static double myPow(double x, int n) {
   if (n < 0) {
       return 1 / fastPow(x, n);
   }
   return fastPow(x, n);
}
public static double fastPow(double x, int n) {
    if (x == 1 || n == 0) return 1.0;
    if (n % 2 == 0) {
        return fastPow(x * x, n / 2);
    }
    return x * fastPow(x * x, n / 2);
}
//方法2
public static double myPow(double x, int n) {
    double res = 1.0;
     /**
     * 以下步骤就是将10进制转为2进制，每次除2的余数
     * 就是从低位到高位的值，每次只可能取0或1。当是
     * 1时就要乘对应位数的次方所以每次都要计算次方确
     * 保余数为1时可以拿来运算
     */
     for (int i = n; i != 0; i /= 2) {
        if (i % 2 != 0) {
            res *= x;
        }
        x *= x;
    }
    return n < 0 ? 1 / res : res;
}

  快速幂模运算就是快速求解a^b % z。利用模运算的分配律,有a^b%z=(a^b/2%z*a^b/2%z)%z(假设b为偶数，奇数则多乘一个a)。那么代入快速乘方运算的模板，就可以得到快速幂模运算，也就是著名的蒙格马利快速幂模算法。

public static int montgomery(int a, int b, int z) {
    int res = 1;
    for (int i = b; i != 0; i /= 2) {
        if (i % 2 != 0) {
           res = (res * a) % z;
        }
        a = (a * a) % z;
    }
    return res;
}