2-2线性回归实现
线性回归实现
%matplotlib inline
import random
from mxnet import autograd, np, npx
from d2l import mxnet as d2l
生成数据集
根据带有噪声的线性模型构造一个人造数据集。
任务是使用这个有限样本的数据集来恢复这个模型的参数。
##使用线性模型参数w=[2,-3.4]T,b=4.2和噪声声项e生成数据集
y = Xw+b+e
###生成一个包含1000个样本的数据集， 每个样本包含从标准正态分布中采样的2个特征。
###标准差设为0.01 num_examples数据集大小 w真实权重，b真实偏移量
def synthetic_data(w, b, num_examples): #@save
"""生成y=Xw+b+噪声"""
###创建均值为0，标准差为1的随机数,行数为样本数，列数是w的长度
X = torch.normal(0, 1, (num_examples, len(w)))
###将X和w相乘，并附加上一个均值为0标准差为0.01的正态分布向量b
y = torch.matmul(X, w) + b
###让y加上一个噪音 形状与y相似 (加噪音是为了防止过度拟合)
y += torch.normal(0, 0.01, y.shape)
###做成列项返回
return X, y.reshape((-1, 1))
###定义真实的w
true_w = torch.tensor([2, -3.4])
##定义真实的b
true_b = 4.2
###生成数据集features特征集合 labels标签集合
features, labels = synthetic_data(true_w, true_b, 1000)
##features中的每一行都包含一个二维数据样本，
## labels中的每一行都包含一维标签值（一个标量）。
###获取特征集和标签集的第一个样本
print('features:', features[0],'\nlabel:', labels[0])
----
features: tensor([ 0.3111, -2.3113]) ###第0个样本
label: tensor([12.6704])
#获取w，b在定义两个真实的w，b 再用真实的值生成数据集
###上述函数说明
torch.normal(mean, std, size)
查看帮助
help (torch.normal)
Example::
>>> torch.normal(2, 3, size=(1, 4))
tensor([[-1.3987, -1.9544, 3.6048, 0.7909]])
mean均值范围和形状，std给出每个均值服从的标准差 size张量的大小
标准差是方差的算术平方根，标准差越小，数据分布越均匀，反之亦然。
是 PyTorch 中的一个神经网络层，用于生成具有正态分布的随机数
值：均值，默认为0 标准差 默认为1 生成器的大小，即列表中元素的数量
torch.normal(3, 0.1, (3, 4))
tensor([[2.8848, 3.0510, 3.0580, 2.9377],
[3.0652, 3.1166, 3.0694, 2.8948],
[3.1655, 3.0748, 2.9984, 3.0817]])
-----
torch.matmul()
用于执行矩阵乘法。
torch.tensor()
张量对象，它表示一个多维数组或矩阵。
torch.tensor([2, -3.4])
tensor([ 2.0000, -3.4000])
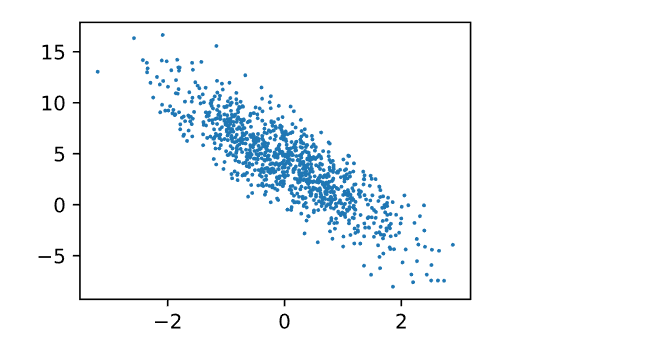
###通过生成第二个特征features[:, 1]和labels的散点图， 可以直观观察到两者之间的线性关系。
d2l.set_figsize()
d2l.plt.scatter(features[:, 1].detach().numpy(), labels.detach().numpy(), 1);
读取数据
该函数能打乱数据集中的样本并以小批量方式获取数据。
该函数接收批量大小、特征矩阵和标签向量作为输入，生成大小为batch_size的小批量。 每个小批量包含一组特征和标签。
###batch_size:批量大小 features:特征集合 labels：标签集合
###定义数据集读取迭代器
def data_iter(batch_size, features, labels):
###计算特征的个数
num_examples = len(features)
###获取所有特征的下标 0- （num_examples-1）
indices = list(range(num_examples))
# 这些样本是随机读取的，没有特定的顺序
random.shuffle(indices) ###把下标打乱
###从0-num_examples 每次跳batch_size大小
# 每次next操作，都会从数据集中返回一个批量的特征和相应的标签集合
for i in range(0, num_examples, batch_size):
batch_indices = torch.tensor(
indices[i: min(i + batch_size, num_examples)])
yield features[batch_indices], labels[batch_indices]
###读取第一个小批量数据样本并打印。
###定义批量大小
batch_size = 10
###获取数据集中的一个批量的特征集合和对应的标签集合
for X, y in data_iter(batch_size, features, labels):
print(X, '\n', y)
break
----
tensor([[ 0.9873, -0.5948], ###10x2
[ 1.3556, 0.3657],
[ 1.5056, 0.2836],
[-0.0573, -0.8181],
[-1.9409, -0.6235],
[ 0.1900, 1.1605],
[ 2.8264, -0.2350],
[ 0.4428, 0.6758],
[-0.4262, 0.2729],
[-0.9610, -0.0114]])
tensor([[ 8.2021], ###10x1
[ 5.6562],
[ 6.2251],
[ 6.8541],
[ 2.4309],
[ 0.6366],
[10.6450],
[ 2.7809],
[ 2.4442],
[ 2.3168]])
初始化模型参数
通过从均值为0、标准差为0.01的正态分布中采样随机数来初始化权重， 并将偏置初始化为0。
###w长为2的向量 requires_grad：计算梯度
w = torch.normal(0, 0.01, size=(2,1), requires_grad=True)
##偏差
b = torch.zeros(1, requires_grad=True)
在初始化参数之后，我们的任务是更新这些参数，直到这些参数足够拟合我们的数据。
每次更新都需要计算损失函数关于模型参数的梯度。 有了这个梯度，我们就可以向减小损失的方向更新每个参数。 因为手动计算梯度很枯燥而且容易出错，所以没有人会手动计算梯度。
定义模型
###定义模型，将模型的输入和参数同模型的输出关联起来。
###X：批量的特征集合 w：随机初始化的权重 b:偏移量
def linreg(X, w, b): #@save
"""线性回归模型"""
###X x w
return torch.matmul(X, w) + b
定义损失函数
###因为需要计算损失函数的梯度，所以我们应该先定义损失函数。
###y_hat：一个批量的预测值 y：一个批量的实际值
def squared_loss(y_hat, y): #@save
"""均方损失"""
return (y_hat - y.reshape(y_hat.shape)) ** 2 / 2
定义优化算法
###（batch_size） 来规范化步长
###params：权重和偏移量 lr：学习率 batch_size：批量大小
def sgd(params, lr, batch_size): #@save
"""小批量随机梯度下降"""
with torch.no_grad():
for param in params:
param -= lr * param.grad / batch_size
param.grad.zero_()
训练
在每次迭代中，我们读取一小批量训练样本，并通过我们的模型来获得一组预测。
计算完损失后，我们开始反向传播，存储每个参数的梯度。
lr = 0.03 ###学习率
num_epochs = 3 ###把整个数据扫3遍
net = linreg ###定义模型
loss = squared_loss ###定义损失函数
###遍历每一轮
for epoch in range(num_epochs):
###遍历每一个批量
###从数据集中取出一个批量的特征集合和对应的标签集合
for X, y in data_iter(batch_size, features, labels):
###求预测损失值
l = loss(net(X, w, b), y) # X和y的小批量损失
# 因为l形状是(batch_size,1)，而不是一个标量。l中的所有元素被加到一起，
# 并以此计算关于[w,b]的梯度
###求和后算梯度
l.sum().backward()
###使用优化器来更新权重和偏移量
sgd([w, b], lr, batch_size) # 使用参数的梯度更新参数
###结束后在整个数据集上计算损失
with torch.no_grad():
###当前训练完成后，利用得到的权重和参数来计算在整个数据集上的损失均值
train_l = loss(net(features, w, b), labels)
print(f'epoch {epoch + 1}, loss {float(train_l.mean()):f}')
----
epoch 1, loss 0.046120
epoch 2, loss 0.000196
epoch 3, loss 0.000051
###计算经过学习后 得到的权重和偏移量与真实值之间的误差
print(f'w的估计误差: {true_w - w.reshape(true_w.shape)}')
print(f'b的估计误差: {true_b - b}')
---
w的估计误差: tensor([-0.0002, -0.0001], grad_fn=<SubBackward0>)
b的估计误差: tensor([0.0005], grad_fn=<RsubBackward1>)
