「从零开始的莫比乌斯反演」1. 线性筛&数论分块

莫比乌斯反演在竞赛中属于数论的内容。虽然说，本系列是想写面向Beginner的教程，但是莫比乌斯反演在数论中并不是很基础的内容，你仍然需要有一定的数论知识的基础。

PS：以下代码都是写博客的时候现场手打的，所以。。。

你需要掌握

• 取模和整除运算的相关知识
• 质数筛法
• 数论分块
• 欧拉函数（可选，最好掌握）

本文只讲数论分块并给出线性筛法的模版。其他内容请自行搜索学习。

线性筛

这里给出线性素数筛：

int prime[maxn], numprime, isprime[maxn];	// isprime[i] == 0：i是素数，反之则不是。prime用来存素数
void make_prime(const int &up_bound) {
    // 从0筛到up_bound，不包含up_bound
    isprime[0] = isprime[1] = 1;
    for (int i = 2; i < up_bound; i++) {
        if (!isprime[i]) prime[numprime++] = i;	// i是素数，放到prime数组里
        for (int j = 0; j < numprime && i * prime[j] < up_bound; j++) {
            isprime[i * prime[j]] = 1;
            if (i % prime[j] == 0) break;
        }
    }
}

数论函数多半与素数有关。所有的积性函数都可以在线性时间内借助素数筛筛出来（这里不理解没关系，后面还会说）。

数论分块

例题

求：

\[\sum\limits_{i=1}^{k}\left\lfloor \dfrac{n}{i} \right\rfloor \]

如果告诉你，\(1 \leq k \leq n \leq 10^6\)，那么，你可以直接枚举。那，如果告诉你，\(1 \leq k \leq n \leq 10^{12}\)呢？

解法

这就要用到数论分块了。数论分块能把复杂度降到\(O(\sqrt{n})\)。原理如下：

我们看几个整数除法的例子：

\(\left\lfloor \dfrac{10}{4} \right\rfloor = 2, \left\lfloor \dfrac{10}{5} \right\rfloor = 2, \left\lfloor \dfrac{10}{6} \right\rfloor = 1, \left\lfloor \dfrac{10}{7} \right\rfloor = 1 \cdots\)

容易发现，总是有这么一段，它们做除法的结果是一样的。比如从\(4\)到\(5\)，除法的结果总是\(2\)；从\(6\)到\(10\)，除法的结果总是\(1\)。

它在图上表示出来是这样的：

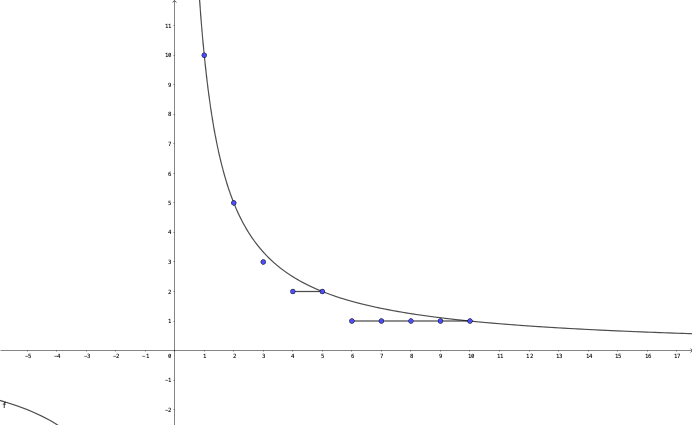
如果我们能把它相等的这一段，直接用乘法求出来，显然会比挨个做加法要快不少。那么，我们如何确定某一段的左右边界呢？

结论

先说结论，最后再说证明。结论很漂亮，但是证明很蛋疼。

\(x = \left\lfloor \dfrac{n}{l} \right\rfloor\)的右边界是\(\left\lfloor \dfrac{n}{\lfloor \frac{n}{l} \rfloor} \right\rfloor\)。

也就是说，对于\(n\)来说，如果\(\left\lfloor \dfrac{n}{l} \right\rfloor = x\)，那么令\(r = \left\lfloor \dfrac{n}{\lfloor \frac{n}{l} \rfloor} \right\rfloor\)，则\(\left\lfloor \dfrac{n}{r} \right\rfloor\)也等于\(x\)。且\(r\)是\(\left\lfloor \dfrac{n}{i} \right\rfloor = x\)的右边界，\(\left\lfloor \dfrac{n}{r + 1} \right\rfloor\)就不等于\(x\)了。

那么，这一段的求和就是\(\left(\left\lfloor \dfrac{n}{\lfloor \frac{n}{l} \rfloor} \right\rfloor - l + 1 \right) \times \left\lfloor \dfrac{n}{l} \right\rfloor\)。

上面提到的例题，代码如下：

for (int l = 1, r; l <= k; l = r + 1) {
    r = min(n / (n / l), k);	// 注意不能超出k
    ans += (r - l + 1) * (n / l);
}

十分简洁。

在不同的地方应用数论分块写起来会有点不同，不过总体上大同小异。

稍微难一点的例题

如果我们要求\(\sum\limits_{i=1}^{k}\left\lfloor \dfrac{n}{i} \right\rfloor \left\lfloor \dfrac{m}{i} \right\rfloor\)呢？

这里会遇到的一个问题就是\(\left\lfloor \dfrac{n}{i} \right\rfloor\)和\(\left\lfloor \dfrac{m}{i} \right\rfloor\)的右边界可能不同。所以，我们只要把这个分段再“切碎一点”就好了。

直接参考代码来理解吧：

for (int l = 1, r; l <= k; l = r + 1) {
    r = min(n / (n / l), m / (m / l));	// “切碎一点”
    r = min(r, k);	// 防止越界
    ans += (r - l + 1) * (n / l) * (m / l);
}

证明

摘自：OI-Wiki

PS：稍微吐槽一下OI-Wiki，OI-Wiki写的内容是很完备而且严谨的，所以对于初学来说反而有点痛苦。。。

PSS：建议做一做OI-Wiki推荐的习题试试： 「luogu P2261」CQOI2007 余数求和

对于任意给定的\(i\)，我们要找一个最大的\(j\)，满足\(\left\lfloor \dfrac{n}{i} \right\rfloor = \left\lfloor \dfrac{n}{j} \right\rfloor\)。

首先，我们证明\(\left\lfloor \dfrac{n}{\left\lfloor \frac{n}{i} \right\rfloor} \right\rfloor \geqslant i\)：

\[\begin{align} & \left\lfloor \dfrac{n}{i} \right\rfloor \leqslant \dfrac{n}{i} \\ \Longrightarrow & \left\lfloor \dfrac{n}{\lfloor \dfrac{n}{i} \rfloor} \right\rfloor \geqslant \left\lfloor \dfrac{n}{\dfrac{n}{i}} \right\rfloor = \lfloor i \rfloor = i \\ \Longrightarrow & i \leqslant \left\lfloor \dfrac{n}{\lfloor \dfrac{n}{i} \rfloor} \right\rfloor = j \end{align} \]

下证明：\(\left\lfloor \dfrac{n}{\left\lfloor \frac{n}{i} \right\rfloor} \right\rfloor\)是满足条件的最大的\(j\)。

设\(k = \left\lfloor \dfrac{n}{i} \right\rfloor\)，那么，必然有\(\left\lfloor \dfrac{n}{j} \right\rfloor = k\)，显然，\(j\)的最大值是\(\left\lfloor \dfrac{n}{k} \right\rfloor\)；

(有一说一，我确实觉得挺显然的)

\(\left\lfloor \dfrac{n}{j} \right\rfloor = k \Longleftrightarrow k \leqslant \dfrac{n}{j} < k + 1 \Longleftrightarrow \dfrac{1}{k + 1} < \dfrac{j}{n} \leqslant \dfrac{1}{k} \Longleftrightarrow \dfrac{n}{k + 1} < j \leqslant \dfrac{n}{k}\)

又因为\(j\)是整数，所以\(j_{max} = \left\lfloor \dfrac{n}{k} \right\rfloor\)