1 神经网络的提出
线性回归和逻辑回归能很好的解决特征变量较少的问题，但对于变量数量增加的复杂非线性问题，单纯增加二次项和三次项等特征项的方法计算代价太高。
2 神经网络算法
2.1 神经元
模拟神经元的模型：
模型的参数即模型的去权重。
2.2 神经网络
如图是一个三层神经网络模型，第一层为输入层，第二层为隐藏层，第三层为输出层。每条边上有一个权值θ。
ai(j)：第j层单元i的“激励”
θ(j)：第j层到第j+1层单元的权值矩阵。
若第j层单元数为sj，第j+1层单元数为sj+1，则θ(j)ϵsj+1∗(sj+1)。
在bp神经网络中，我们使用sigmoid函数作为激励函数。即 
，也就是我们逻辑回归中使用的函数。
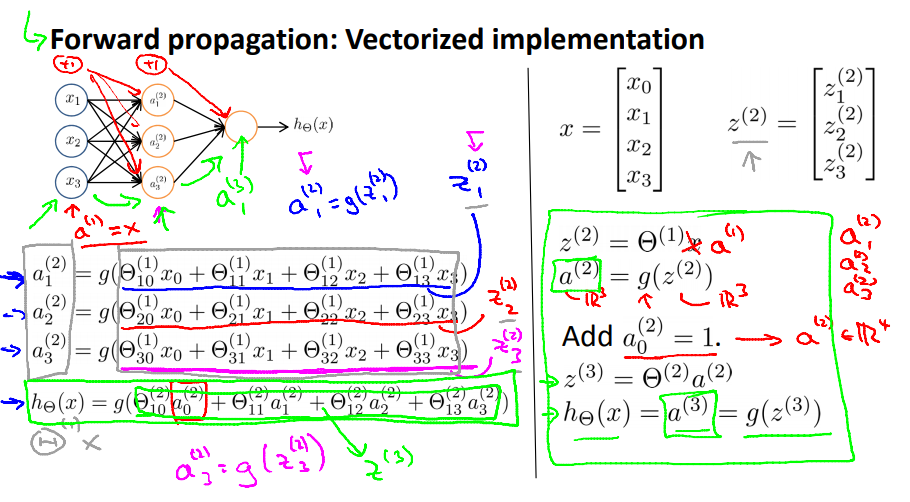
记住：z(j)=Θ(j−1)a(j−1)。然后：a(j)=g(z(j))。
前向传播：从输入层到隐藏层再到输出层依次计算激励的过程叫前向传播。
3 应用
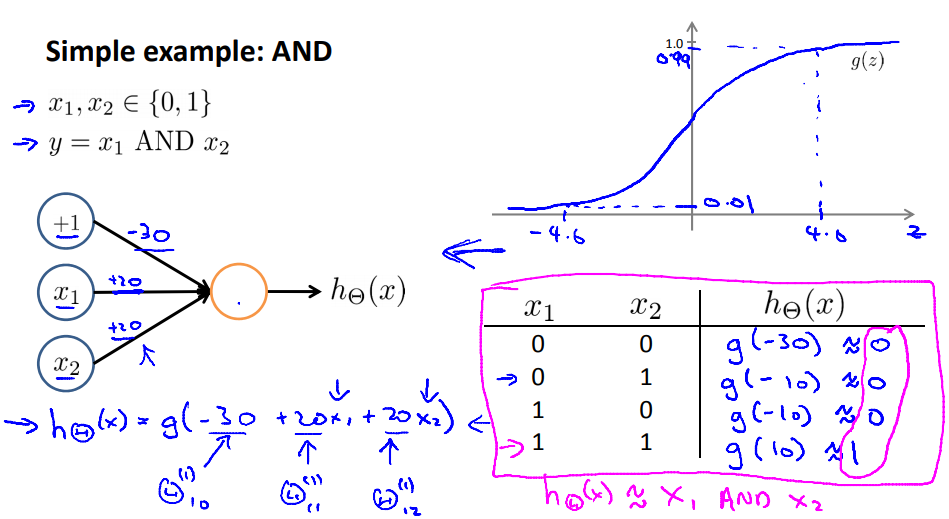
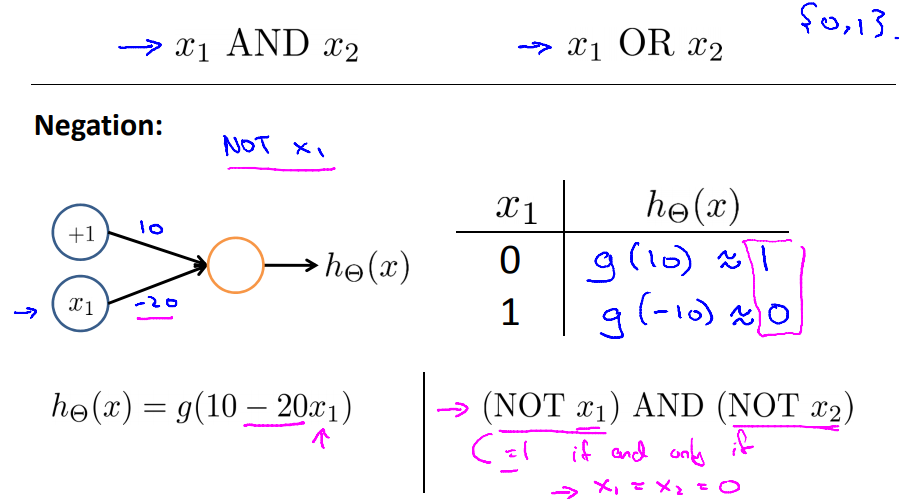
3.1 and 、 or、非运算
3.2 组合
三个式子合起来，可以求更复杂的线性函数（X1 xnor X2）。
可以理解为：
通过组合不同计算功能的神经元，我们可以使神经网络表示复杂的表达式。——CREAT TANG
3.3 多分类
作业三：多类分类和前馈神经网络
https://blog.csdn.net/cowry5/article/details/80367832
