1 逻辑回归
1. classification 分类
eg:垃圾邮件分类、交易是否是欺诈、肿瘤类别。分类的结果是离散值。
2. sigmoid函数

使用线性方法来判断分类问题,会出现上图中的问题,需要人工判断分界点。有些特殊的样本点,也会使得分界点发生漂移,影响准确性。我们希望我们的分类器输出范围在0~1之间,此时分类问题转化为边界问题。sigmoid函数能保证数据在0~1之间,并且越趋近于无穷大,输出趋近于1。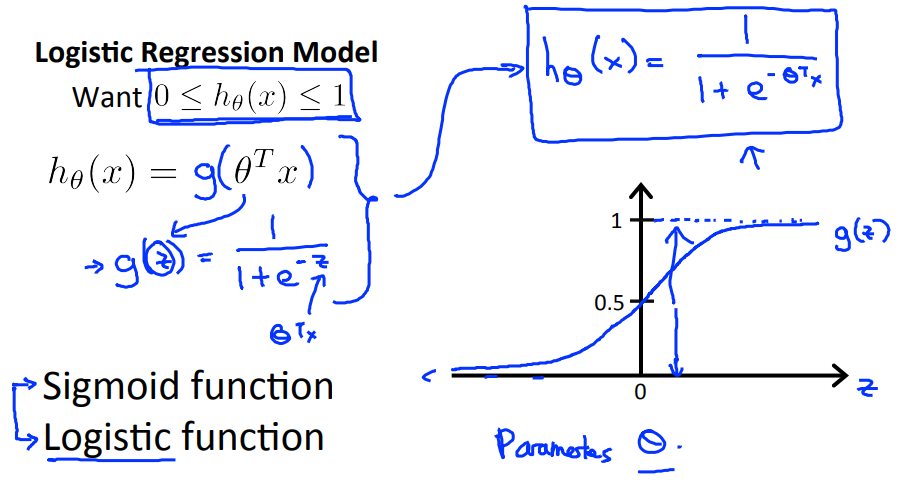
假设函数预测的是对于输入x,输出为1的概率。
3. cost function
如果代价函数依然采用平方误差函数,得到的是一个non-convex函数,此时梯度下降无法保证收敛得到全局最优值。因此我们用另一种方式表示cost function,使它作为convex函数,易于求解。
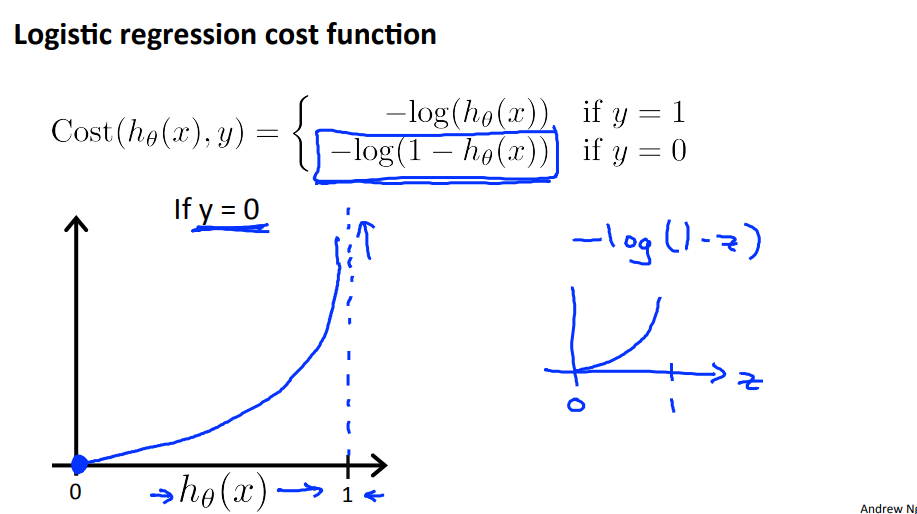
如果把代价函数定义为上述形式,当真实的值是1时,我们预测的值越靠近1,cost的值越小,误差越小。如果真实值是0,那么预测的值越靠近1,cost的值越大。
简化公式:
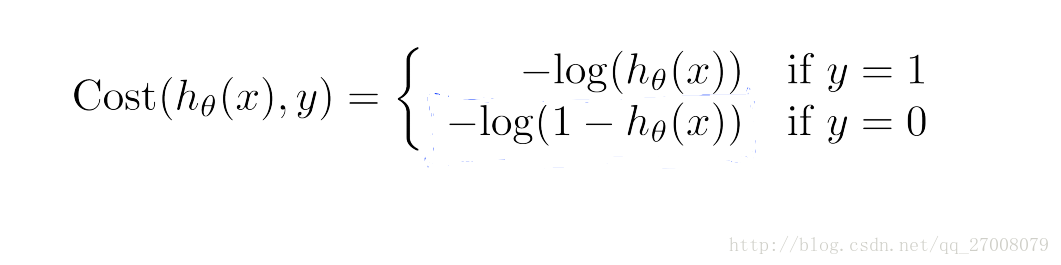
4. 梯度下降
一般形式:

计算微分部分得到:
5. 高级优化方法
“共轭梯度Conjugate gradient”,“BFGS”和“L-BFGS” 是可以用来代替梯度下降来优化θ的更复杂,更快捷的方法。
都是求J函数和偏导数,然后进行优化。后三个算法优点:都不需要手动选择学习率阿尔法(他们有内部循环,线性搜索算法,可以自动尝试学习率,并选择最好的学习率);它们的收敛速度往往比梯度下降要快。缺点:更复杂
6. 多分类问题
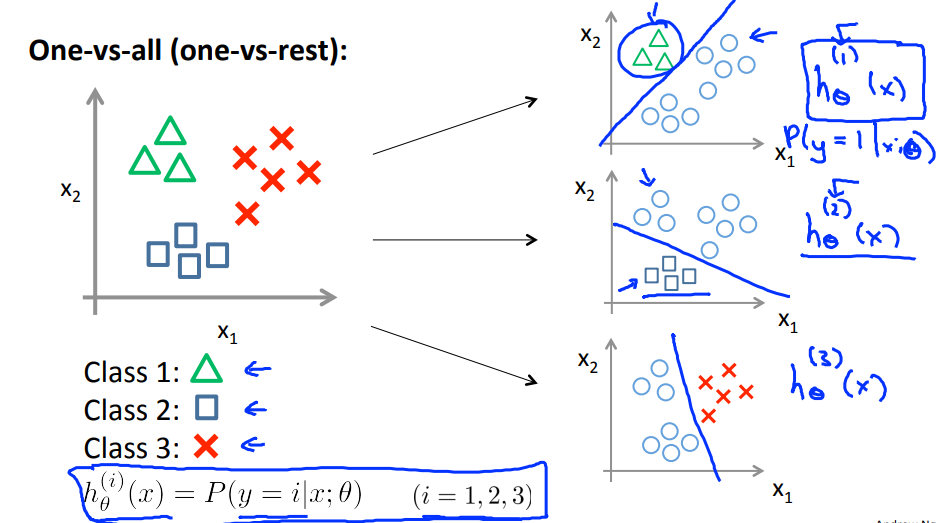
可以理解为采用多个Losgistic分类器进行分类,针对每个样本点进行一次预测,选择概率值最大的那个。
2 正则化
1. 过拟合
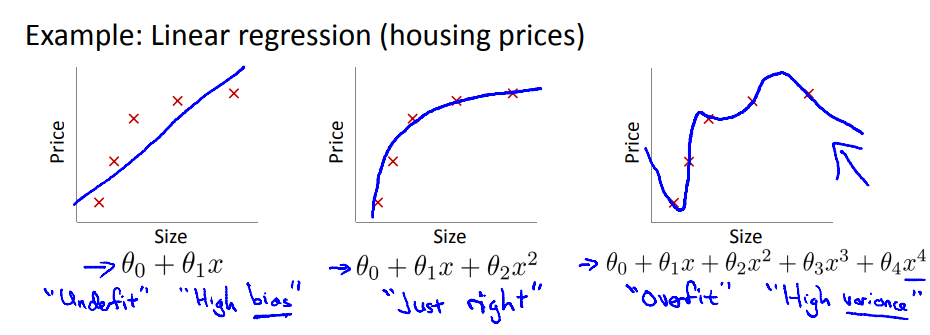
图一 欠拟合,高偏差。图三 过拟合,高方差。
2 解决方法
1. 减少特征的数量,可以通过一些特征选择的方法进行筛选。
2. 正则化,通过引入一个正则项,限制参数的大小。
3 正则化用于线性回归
4 正则化用于逻辑回归
比如下面的曲线,针对高次项的参数,在后面多加一项乘以1000。这样在优化损失函数的时候,会强制θ3和θ4不会很大,并且趋近于0,只有这样才会保证损失函数的值足够小。

得到的公式如下,注意只会针对x1开始,θ0相当于只是针对偏置项设置的,因此不需要加正则项。
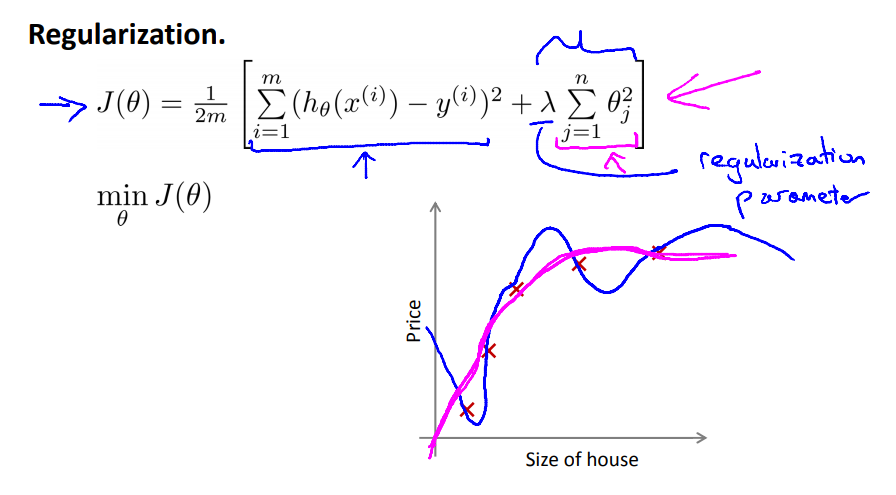
但是如果λ设置的过大,相当于所有的θ都变成了0,损失函数的曲线相当于一条直线,就没有任何意义了,因此选择适合的λ很重要,后面也会讲解如何选择正确的λ。
5 梯度下降
添加正则项之后,梯度下降的公式就发生了变化:
3 编程作业——实现logistic regression
还有很多看不懂的地方,这两篇博文说的很详细:
https://blog.csdn.net/Cowry5/article/details/80247569
https://blog.csdn.net/u012052268/article/details/78653293


