1 多元线性回归
1.1 假设函数
多元线性回归是指有多个特征特征变量的情况。此时我们修改假设函数hθ(x)=θ0+θ1∗x为hθ(x)=θ0+θ1x1+θ2x2+⋯+θnxn。
设x0=1,x为特征向量,θ为参数向量,则hθ(x)=θTx。
1.2 cost function与梯度下降
cost函数依然选择平方误差函数
梯度下降方法也没有变:

1.3 特征约简
当变量的范围差别很大时,梯度下降法就会收敛的很慢,此时我们使输入的变量大致属于相同的范围来加速梯度下降。
两种方法:特征缩放、均值归一化(x-μi)/最大值
1.4 多项式回归
有时候曲线能更好的拟合数据,这时可以采用多项式回归。
假设函数为: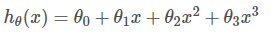
设x2=x12,x3=x13。则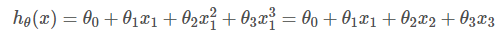 。
。
这样就把多项式回归转变成了多参数线性回归。
2 正规方程
1. 梯度下降要设置α并不保证一次能获得最优的α,正规方程不用考虑α。
2. 梯度下降要迭代多次,正规方程不用。(所以,遇到比较简单的情况,可用正规方程)
3. 梯度下降最后总能得到一个最优结果,正规方程不一定。因为正规方程要求X的转置乘X的结果可逆。
4. 当特征数量很多的时候,正规方程计算不方便,不如梯度下降。
3 Octave 基础教程
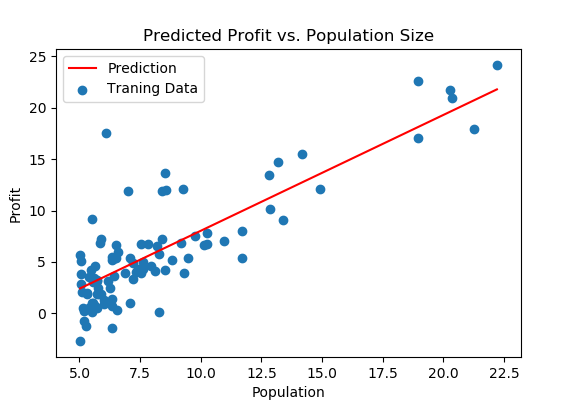
4 编程作业——实现线性回归
代码和解释详见 https://blog.csdn.net/Cowry5/article/details/80174130。
实验结果: