B-spline Curves: Computing the Coefficients
本博客转自前人的博客的翻译版本，前几章节是原来博主的翻译内容，但是后续章节博主不在提供翻译，后续章节我在完成相关的翻译学习。
（原来博客网址：http://blog.csdn.net/tuqu/article/details/4749586）
原来的博主翻译还是很好的，所以前几章节直接借鉴参考原博主的内容。
尽管de Boor算法是一个计算对应于给定u的B-样条曲线上的点的标准方法， 我们许多情况下（例如，曲线插值和逼近）真正需要的是这些系数。我们将阐述一个简单方法来做这个。
给定一个由 n+1个控制点P0, P1, ..., Pn, 和 m+1个节点 u0=u1=...=up=0, up+1, up+2, ..., um-p-1, um-p=um-p+1=...= um=1定义的p 次clamped B-样条曲线。对于任何给定在[0,1]上的 u ，我们想计算系数N0,p(u), N1,p(u), ..., Nn,p(u) 。一个简单方法是使用下列递推关系：
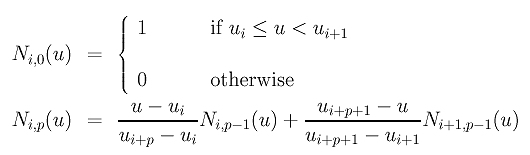
但是这是一个非常耗时的过程。为了计算 Ni,p(u), 我们需要计算 Ni,p-1(u)和Ni+1,p-1(u). 为了计算Ni,p-1(u), 我们需要计算Ni,p-2(u) 和 Ni+1,p-2(u). 为了计算Ni+1,p-1(u), 我们需要Ni+1,p-2(u)和 Ni+2,p-2(u). 如你们所看到的， Ni+1,p-2(u)出现了两次，因此，递归计算会重复。当递归继续深入，会出现更多的重复计算。这与在前页讨论的de Casteljau算法的递归版本很相似。因此，计算速度非常慢。
有容易的方法。设 u 在节点区间[uk,uk+1)上。. B-样条基函数的重要性质 说明最多 p+1个p 次基函数在[uk,uk+1)上非零，即： Nk-p,p(u), Nk-p+1,p(u), Nk-p+2,p(u), ..., Nk-1,p(u), Nk,p(u)。通过定义，在 [uk,uk+1)上的0次仅有的非零基函数是Nk,0(u)。结果，从.Nk,0(u)出发计算系数是以一个 "fan-out" 三角形式，如下图所示：
因为在 [uk,uk+1)上 Nk,0(u) = 1而其他0次B-样条基函数在[uk,uk+1)上是零，我们可以从 Nk,0(u)开始而计算1次基函数 Nk-1,1(u) 和 Nk,1(u)。从这两个值，我们可以计算2次基函数 Nk-2,2(u), Nk-1,2(u) 和Nk,2(u)。这个过程重复直到所有p+1 个非零系数计算出来。
在这个计算中， “内部”值如 Nk-1,2(u)有一个西北向前驱 (即， Nk-1,1(u))和一个西南向的前驱 (即， Nk,1(u))；上述三角如Nk-1,1(u)的东北方向边界上的值只有一个西南向前驱 (即， Nk,0(u))；这个三角如 Nk,2(u)的东南方向边界上的值只有一个西北前驱 (即， Nk,1(u))。因此， 在东北 (resp., 东南)方向边界上的值使用定义中的递归关系的第二 (resp., 第一)项 。只有内部值使用全部两项。基于这个观察，我们有下列算法：
上述算法不是很有效的算法。它的目的是为了以一个直觉容易理解的方式说明思想。 数组N[ ] 保存所有中间值和最后结果。对一个次数 d, N[i] 保存了Ni,d(u)的值，且，最后，N[k-d], N[k-d+1], ..., N[k] 含有非零系数。计算以 d=1开始因为我们知道仅有的非零基函数是 Nk,0(u)如果 u 在节点区间 [uk,uk+1)上。 外循环使得次数 d 从 1到 p。 begin 后面的第一次赋值是仅使用一项(即，三角中的西南项， Nk-d+1,d-1(u))，计算 Nk-d,d(u) ， 内部 for 循环计算 “内部”项，而外循环中最后一个语句仅使用一项(即，三角中的西北项， Nk,d-1(u)) 计算 Nk,d(u)。
你能使这个算法更有效吗?
B-spline Curves: A Special Case
B-样条曲线：特例
如果我们有 2n+2 个节点 u0 = u1 = ... = un = 0及 un+1 = un+2 = ... = u2n+1 = 1 (即，头 n+1 个是零，而后 n+1是1)， n 次B-样条基函数是什么？
因为每个 u 在 [0,1] = [un, un+1]上， n 次非零基函数是： N0,n(u), N1,n(u), ..., Nn,n(u)。回忆B-样条基函数的定义如下：
因为仅有的 0次非零基函数是Nn,0(u)，下标 i 只能在0 和n之间。因此， ui是零而 ui+n和ui+n+1是1。结果，上边第二个等式可重写为如下式：
如果我们进行如前页讨论的那样以一个三角形式计算N0,n(u), N1,n(u), ..., Nn,n(u) ，那么我们有下图。在该图中，每个东北(resp., 东南)边界箭头意味这乘1-u (resp., u)到在箭头尾部的项上。注意计算中有n 步骤，每步获得每列。因此， Nn,0(u) 对 N0,n(u)的贡献是 (1-u)n, 而Nn,0(u)的贡献对Nn,n(u)是un.
现在，考虑一般项 Ni,n(u)的计算。 Nn,0(u) 对Ni,n(u)计算的贡献可用"path-counting"技术确定，其用来展示de Casteljau算法的正确 以及贝塞尔曲线的更高次导数的计算中。每个从 Nn,0(u) 到 Ni,n(u) 遇n 箭头其中i 是东南边界 而 n-i 是东北边界。 那些东北(resp., 东南)边界箭头意味着对尾部的项乘以1-u (resp., u)。因此，Nn,0(u) 对 Ni,n(u)的贡献沿着一个单path是 ui(1-u)n-i 。从 Nn,0(u) 到 Ni,n(u)的paths总数是C(n,i)。更准确地，paths的数目等于放置 i 个东南边界箭头在n 个位置不同方法的数目。剩余 n-i 位置用东北边界箭头充满。这 n 个箭头准确地描述了从 Nn,0(u) 到 Ni,n(u)的一个单路径（path）。因为每个路径（path）贡献 ui(1-u)n-i 给计算且因为有C(n,i) 个路径，Nn,0(u) 对 Ni,n(u)的总贡献是
这就是 n次第i个贝塞尔基函数。因此，我们有下列结论：
