MOS管常用效应
沟道长度调制效应(channel length modulation)
短沟道情况, 沟道长度调制效应越明显,λ越小,Id越大
MOS晶体管中,栅下沟道预夹断后,若继续增大Vds,夹断点会略向源极方向移动,导致夹断点到源极之间的沟道长度略有减小,有效沟道电阻也就略有减小,从而使更多电子自源极漂移到夹断点,导致在耗尽区漂移电子增多,使Id增大,这种效应称为沟道长度调制效应

漏极导致势垒下降(drain induced barrier lowering)
形成反型层之后,反型层越厚,导电沟道电阻减小,阈值电压Vth减小
当在MOS管的漏极加电压时,漏极和衬底构成的pn结,漏极一侧会出现正电荷堆积,相应的,衬底一侧会感应出负电荷,这些负电荷有助于沟道的形成,因此导致阈值电压相对减小,这种效应称为漏极导致势垒下降
衬底电流体效应(substrate current body effect)
形成反型层之前,耗尽层越厚,阈值电压Vth增加
类似我们常说的雪崩倍增效应。先讲热电子,所谓热电子,是指电子在两次散射间获得的能量将可能超过它在散射中失去的能量,从而使一部分电子的能量显著高于热平衡时的平均动能而成为热电子。
当在MOS管的漏极加很高的电压,形成强电场的情况下,衬底中的热电子越过漏极与衬底之间的势垒进入漏极,热电子与晶格碰撞,产生电子和空穴对,电子流向漏极而空穴流向衬底,形成漏极与衬底之间的电流。如果不断累积,形成大电流,则称之为衬底电流体效应。
通常,在现代工艺的基础上,当Vds上升至1.5~2v时,就有可能出现这个效应,这三种效应是在不断增加漏极电压的情况下逐渐变为主导效应的。
通常analog design习惯应用CLM以及DIBL为主导效应的区域,因为在SCBE区域,输出电阻将会大大的减小。
但实际上目前analog design主要应用的还是CLM的区域。 需要注意的是,在CLM区域,输出电阻不是恒定值,而是随漏极电压的变化而变化的。
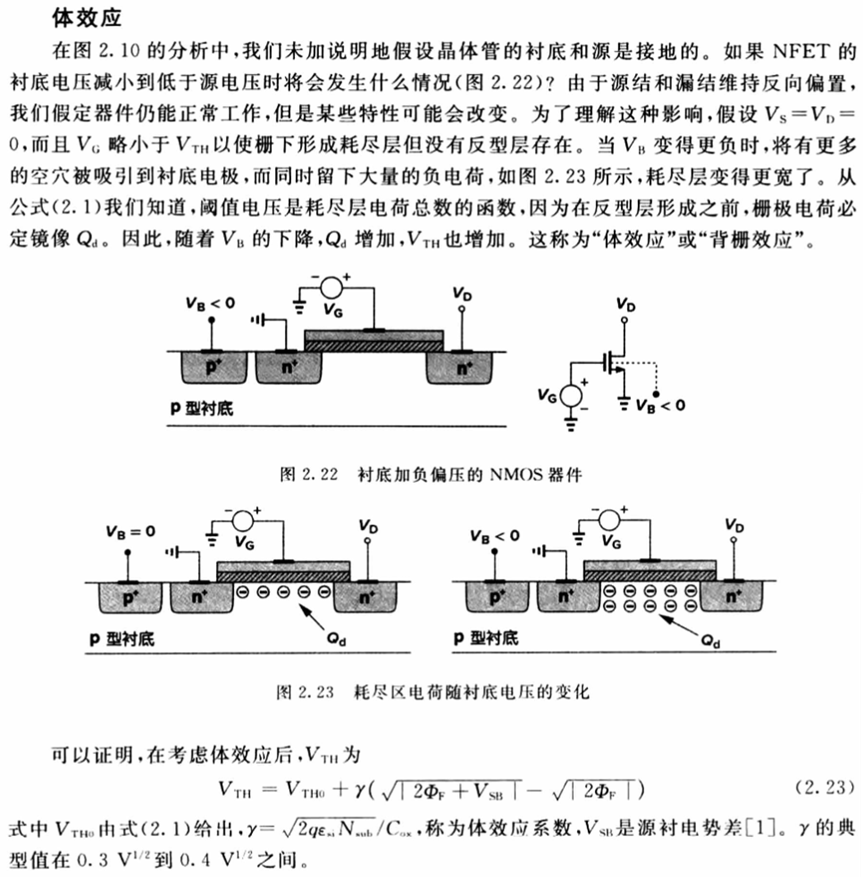
MOS晶体管的衬底偏置效应(体效应)
形成反型层之前,耗尽层越厚,阈值电压Vth增加
处于反偏的PN结的耗尽层将展宽。 在实际工作中,经常出现衬底和源极不相连的情况,此时,VBS不等于0。
由基本的pn结理论可知,处于反偏的pn结的耗尽层将展宽。当衬底与源处于反偏时,衬底中的耗尽区变厚,使得耗尽层中的固定电荷数增加。
由于栅电容两边电荷守衡,所以,在栅上电荷没有改变的情况下,耗尽层电荷的增加,必然导致沟道中可动电荷的减少,从而导致导电水平下降。若要维持原有的导电水平,必须增加栅压,即增加栅上的电荷数。
对器件而言,衬底偏置电压的存在,将使MOS晶体管的阈值电压的数值提高。
对NMOS,VTN更正,对PMOS,VTP更负,即阈值电压的绝对值提高了。
△VT=±γ√|Vbs| γ为衬底偏置效应系数,它随衬底掺杂浓度而变化
典型值:NMOS晶体管: 0.7~3.0; PMOS晶体管:0.5~0.7 △VT为阈值电压变化量。
对PMOS晶体管,取负值,对NMOS晶体管,取正值。
亚阈值导电性(Subthreshold conductivity)
当 MOSFET 的 Vgs 接近其阈值电压 Vth 时,MOS 管工作在亚阈值区(或弱反型区),在结构上类似于两个背靠背的二极管相连。
弱反型区适合低功耗电路,因为电流很小,但问题在于较大的噪声以及低速。
亚阈值电流(subthreshold leakage)
别名:亚阈值漏电流
如果是在MOS管理想的电流-电压特性中,当Vgs<Vth 时,漏极电流 Id 为0,此时会认为MOS管不导通。而实际情况是,当Vgs<Vth 时,MOS晶体管处于表面弱反型状态,这个区域叫做亚阈值区。MOS管工作在亚阈值区时,沟道中虽然存在反型载流子,但浓度较低,因而此时 Id 很小,但不为0,源极和漏极之间的微量漏电流,此电流称为亚阈值电流。
强反型区(Vgs>Vth完全导通,大导电沟道)
MOS的导通就是在栅极的控制下,Vgs比较小时,靠近栅极附近形成负离子区(耗尽层),Vgs逐渐增大时,耗尽层越来越厚,衬底的自由电子会被吸引到栅极与耗尽层之间形成负电子区(反型层),负电子区形成导电沟道,此时的反型层是强反型层,此时的Vgs电压就是阈值电压。
弱反型区(Vgs<Vth不导通,小导电沟道)
如果Vgs<Vth时,栅极与耗尽层之间也有负电子,但是由于Vgs比较小吸引过来的负电子很少,存在很窄的导电通道,Id 很小,但不为0,此时的反型层是弱反型层,即亚阈值区。
因为反型层的出现本质上是个载流子的热运动过程,这一过程是不能突变的,只能是随时间的逐渐积累,当积累到一定程度认为器件”导通”,但不能认为在达到阈值之前器件是完全关断的。这里要牵扯到由mos管电容模型推导出的“亚阈值摆幅”——一个专门衡量器件在亚阈值区特性的参数。
亚阈值摆幅(Subthreshold swing)
亚阈值摆幅,又称为S因子,这是MOSFET在亚阈状态工作时、用作为逻辑开关时的一个重要参数。
定义为:
S在数值上就等于为使漏极电流Id变化一个数量级时所需要的栅极电压增量ΔVgs,注意S是从Vgs-Id曲线上的最大斜率处提取出来的,表示着Id~Vgs关系曲线的上升率。
为了提高MOSFET的亚阈区工作速度,就要求S值越小越好,为此应当对MOSFET加上一定的衬偏电压和减小界面陷阱。S值越小,栅极电压增量ΔVgs越小。
我们希望亚阈值摆幅越小越好;器件在亚域区,即栅压小于阈值电压时,器件完全关断,源漏电流为零。一到阈值电压,晶体管迅速打开;所以最好电流相对于电压变化是非常灵敏的,也就是很小的栅极电压变化就可以引起电流一个数量级的变化。因此S小,反映了更好的栅控能力,小的亚阈值漏电流。
既然有很小的漏电流,亚阈值mos管就可以看作"导通",就可以产生跨导gm,有gm有Rout就有gain。
亚阈值摆幅影响因素
亚阈值电流和饱和电流的区别
- 当Vgs与Vth之间的关系使MOS管弱反型,那么Vds无论怎么变,MOS管要么截止(Vgs<<Vth),要么工作在亚阈值区(Vgs<Vth),大大增大了信号的输入范围。
- 由于亚阈值电流是扩散电流,那么受沟道调制也比较小,电流稳定性也非常好。但是扩散电流的电流值很小,并且启动速度很慢,这也是亚阈值区带来的一些问题。
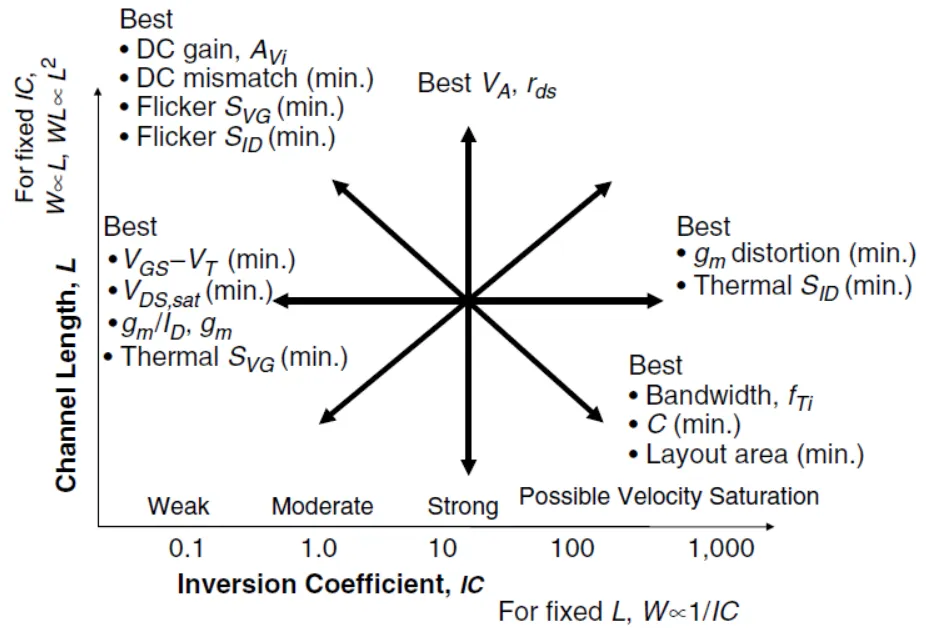
- 饱和区(Vgs>Vth)和亚阈值区(Vgs<Vth)的主要区别是Vgs与Vth的相对大小,分别对应与强反型和中等~弱反型。但它们都存在漏极电流饱和,因此都有对应的Vdsat。基于gm/Id或IC的设计方法,已经不再特别区分这两个区域,而是在all-region上都可以做设计,并且通常在中等反型区具有较好的功耗速度的折衷。
 D. M. Binkley, Trade-offs and optimization in analog CMOS design. Chichester, England ; Hoboken, NJ: John Wiley & Sons, 2008.
D. M. Binkley, Trade-offs and optimization in analog CMOS design. Chichester, England ; Hoboken, NJ: John Wiley & Sons, 2008.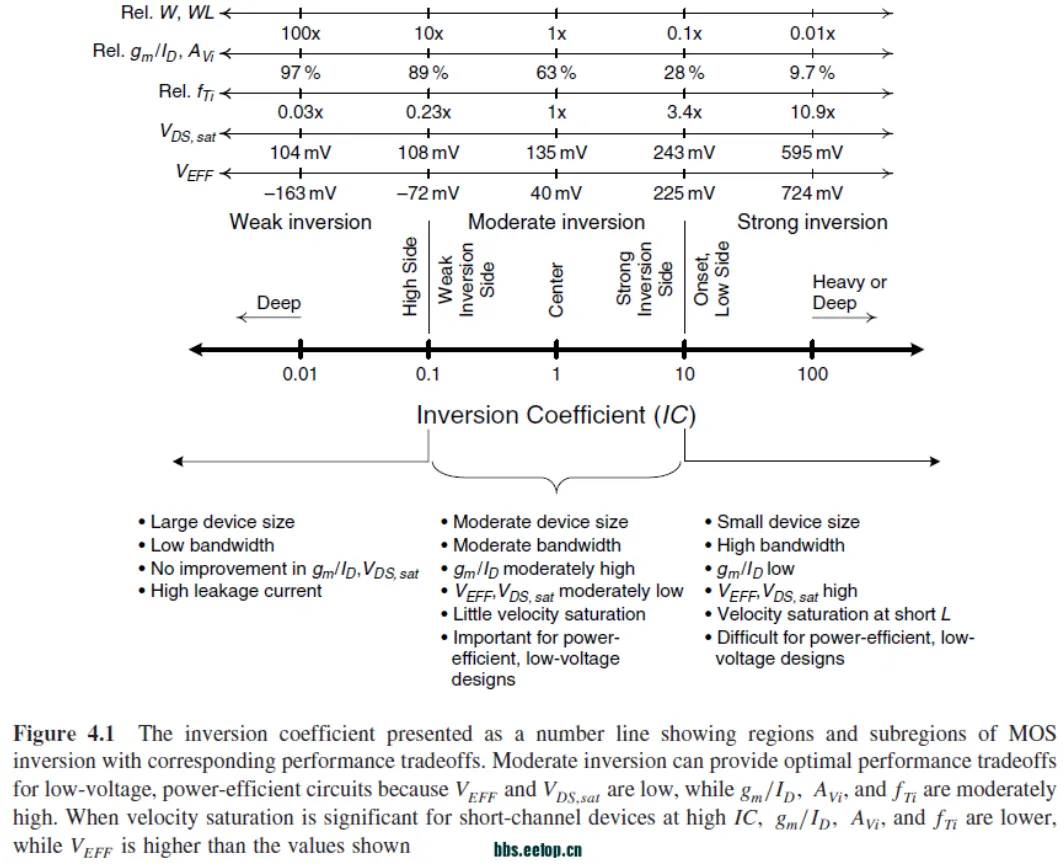 D. M. Binkley, Trade-offs and optimization in analog CMOS design. Chichester, England ; Hoboken, NJ: John Wiley & Sons, 2008.
D. M. Binkley, Trade-offs and optimization in analog CMOS design. Chichester, England ; Hoboken, NJ: John Wiley & Sons, 2008.亚阈值区MOS管的跨导电流比最高,为什么运放里面还是用饱和区呢
-
关于工作区,小电流也可以用倒比管工作在饱和区,不一定电流小就一定工作在亚阈值区;
-
关于带宽,如果电流不变,增加输入管size,gm会增大,这样带宽就会宽一点,付出的代价是失调offset变大,原因是亚阈值区的指数特性,或者说BSIM model 有个参数,跑offset,vgt 接近-50mV 应该就会很明显;一般Vth 失调用avth计算的结果此时会失效;
-
关于mismatch电流镜提高mismatch的方法是,提高Vdsat和增加面积;如果gm退化,降低Vdsat,那么mismatch 就会恶化,一般都是伴随着增加面积,所以看起来不太明显,如果保持面积不变,降低Vdsat,此时mismatch 应该会比较明显。基于第二条,亚阈值区matching 特性比较差;
跨导-
关于噪声,实测结果,亚阈值区的噪声model偏小,实际噪声可能会大很多;一般工艺中flicker noise仿真结果, pmos 优于nmos,native 优于pmos(这个我不认同,个人也没有实测数据,工艺厂给的文档是在饱和区测得);
结论:-
无论是输入对管还是负载电流镜管,用偏置在亚阈值区的管子,matching 首先会限制;
-
其次,亚阈值区时其他效应影响会变大,导致模型不够准确,仿真结果和测试结果差异过大;
- 最后,留意噪声,虽然这个参数一般不是很重要;
- 有时候需要工作在亚阈值区的运放,比如低压低功耗的BGR就很适合亚阈值的运放,电流小,功耗小,虽然牺牲了带宽,但是无妨。低速低功耗应用用亚阈值还是比较常见。但是
1、偏置在亚阈值区工作很难保证2、亚阈值区工作的运放响应速度不快3、运放有些偏置考虑到噪声、匹配等并不希望工作在跨导电流比高的场合虽然亚阈值的gm/Id相对较大,相同电流的gm大;但是打个比方,w翻一倍,面积大一倍,电容大一倍,gm/Id假如从20到25,从速度ft来看还是吃亏的;
MOS管的三个工作区域状态分析
MOS管三个工作区为完全导通区、截止区、线性区MOSFET工作区域的判定方法(NMOS):当 Vgs < Vth 时,截止区。当 Vgs > Vth 且 Vds < Vgs - Vth 时,变阻区。当 Vgs > Vth 且 Vds > Vgs - Vth 时,饱和区(恒流区)。PMOS比较绝对值即可!其中 Vth 是 MOS管 的一个重要参数——开启电压。当MOS管 工作在变阻区内时,其沟道是“畅通”的,相当于一个导体。在 Vds Vds < Vgs - Vth时近似满足V-I的线性关系,即有一个近似固定的阻值。此阻值受 Vgs 控制,故称变阻区域。MOS管 工作在饱和区(恒流区)与 BJT 的饱和区不同,称 MOS管此区为饱和区,主要表示 Vds 增加 Id 却几乎不再增加——也即电流饱和。其实在此饱和区内,MOS管 和 BJT 都处于受控恒流状态,故也称其为恒流区。N沟道增强型MOS管的四个区域
1)可变电阻区(也称非饱和区)
满足Ugs>Ugs(th)(开启电压),Uds<Ugs-Ugs(th),为图中预夹断轨迹左边的区域其沟道开启。在该区域Uds值较小,沟道电阻基本上仅受Ugs控制。当Ugs一定时,Id与Uds成线性关系,该区域近似为一组直线。这时场效管D、S间相当于一个受电压Ugs控制的可变电阻。2)恒流区(也称饱和区、放大区、有源区)
满足Ugs≥Ugs(th)且Uds≥Ugs-Ugs(th),为图中预夹断轨迹右边、但尚未击穿的区域,在该区域内,当Ugs一定时,Id几乎不随Uds而变化,呈恒流特性。Id仅受Ugs控制,这时场效应管D、S间相当于一个受电压Ugs控制的电流源。场效应管用于放大电路时,一般就工作在该区域,所以也称为放大区。3)夹断区(也称截止区)
夹断区(也称截止区)满足Ugs<Ugs(th)为图中靠近横轴的区域,其沟道被全部夹断,称为全夹断,Id=0,管子不工作。4)击穿区
击穿区位于图中右边的区域。随着UDs的不断增大,PN结因承受太大的反向电压而击穿,ip急剧增加。工作时应避免管子工作在击穿区。转移特性曲线可以从输出特性曲线。上用作图的方法求得。例如在图( a)中作Ugs=6V的垂直线,将其与各条曲线的交点对应的Id、Ugs值在Id- Ugs 坐标中连成曲线,即得到转移性曲线,如图(b)所示。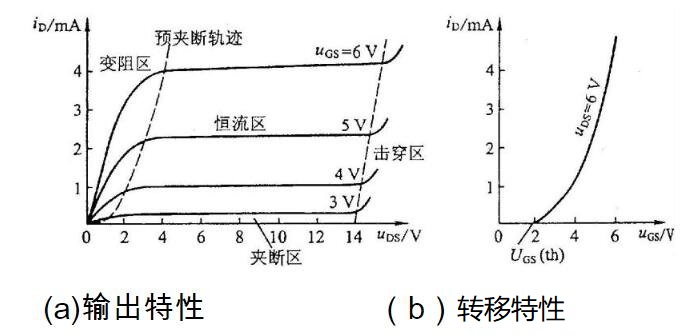
速度饱和区(短沟道和大过驱动电压器件)
速度饱和区沟道电场很强,所有电子以最大速度运动,跨导gm与沟道长度无关且这是MOS管能达到的最大跨导。由于跨导不变,消耗的电流Ids却在增加,一般不设计MOS管工作在这一区。Vdsat=Vgs-Vth 是一个基于沟道夹断的近似模型,判断饱和实际上并不是很准确,尤其是在短沟道器件、FINFET器件误差会较大,实际的Vdsat会比这个值更小。对于长沟道器件
沟道夹断模型认为当Vds≥Vgs-Vth 时,Vgd小于Vth,饱和区,漏端已经不能形成反型层,沟道在漏端发生夹断。由于夹断区场强很大,所以虽然没有沟道依然会把沟道里的载流子强行拉过耗尽区进入漏极。此时额外的Vds电压全部落在夹断区的耗尽层上,所以电流不随Vds增大(不考虑沟长调制效应)。对于短沟道器件
而短沟道器件由于场强较大,速度饱和效应可能先于沟道夹断导致电流饱和。速度饱和效应是指载流子迁移率随着电场强度上升而下降,导致载流子平均速度存在一个极限,无法随着电场强度无限增加。当电场强度达到临界饱和场强Ec时,载流子到达速度极限,此时电流就不会随着Vds的增加而增加了,mos管也就进入了饱和区。总结
所以理论上当沟长L乘以材料的饱和临界场强Ec远大于Vgs-Vth的时候(长沟器件),沟道夹断模型更合理;当沟长L乘以材料的饱和临界场强Ec远小于Vgs-Vth的时候(短沟器件),速度饱和模型更合理。实际使用
实际上现在的工艺无论是用沟道夹断模型还是速度饱和模型都不是很精确,所以又有了两区模型——把沟道划分为强场区和弱场区,分别应用速度饱和模型和沟道夹断模型。所以现在的仿真模型都是直接测量后数值拟合了,不再试图根据物理效应来建模。-
在经典的模拟电路中,晶体管一般要求工作在饱和区,为了减小电路失配(mismatch)和沟道长度调制效应的影响,晶体管的沟道长度L一般比较大,即为长沟道器件。
-
作为电流镜的晶体管,要尽可能地减小沟道长度调制效应的影响,晶体管尺寸L比较大(同时减小失配),但是宽长比W/L一般不大,过驱动电压Vgs-Vth适中,晶体管工作在强反型区,Vdsat取150mV-200mV左右。
-
做为运放的输入对管,对增益gm和电路失配的要求比较高,晶体管尺寸W和L比较大(减小失配),同时宽长比W/L比较大(增加gm),因此过驱动电压Vgs-Vth一般很小,晶体管工作在弱反型区,Vdsat取150mV左右,很难做到更大。
为了保证晶体管可靠地工作在饱和区,Vds与Vdsat的差值要足够大,一方面是担心工艺偏差导致晶体管进入线性区,另一方面晶体管工作在饱和区附近,Rds比较小,晶体管的本征增益比较小。常规情况下,Vds-Vdsat至少要为100mV,最好为200mV左右。公式推导和图:什么是速度饱和效应
在半导体器件中,载流子在外加电压时,受到电场力的作用而定向移动,形成漂移电流,载流子的平均漂移速度𝒗与电场强度E成正比,比率就是载流子迁移率当载流子迁移率u减小时,将更不容易发生速度饱和。实际上,载流子迁移率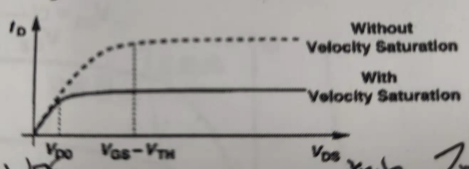 当MOS管发生速度饱和时,我们可以写出漏极速度饱和电流为:
当MOS管发生速度饱和时,我们可以写出漏极速度饱和电流为: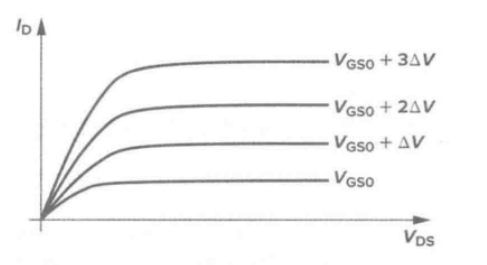 如上图所示,此时的漏极电流与过驱动电压呈线性关系,而不是平方关系。我们可以用这种线性关系来表示发生了速度饱和,饱和区MOS管IV特性也可能介于线性与平方关系之间。载流子迁移率
如上图所示,此时的漏极电流与过驱动电压呈线性关系,而不是平方关系。我们可以用这种线性关系来表示发生了速度饱和,饱和区MOS管IV特性也可能介于线性与平方关系之间。载流子迁移率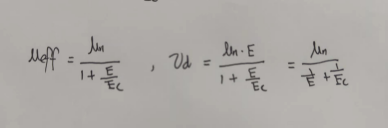
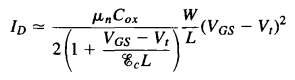 或者:(拉扎维-模拟CMOS集成电路设计)
或者:(拉扎维-模拟CMOS集成电路设计)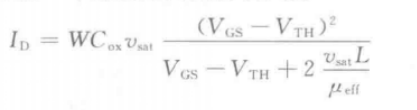 两者可化简为同一公式(分母系数有点差异),从上面两式以及对横向电场的分析可知,当L足够大时或者Vgs-Vth足够小时,MOS管将不易发生速度饱和,更一般的,饱和区漏极电流将更符合平方关系。载流子迁移率同样也受纵向电场作用:
两者可化简为同一公式(分母系数有点差异),从上面两式以及对横向电场的分析可知,当L足够大时或者Vgs-Vth足够小时,MOS管将不易发生速度饱和,更一般的,饱和区漏极电流将更符合平方关系。载流子迁移率同样也受纵向电场作用: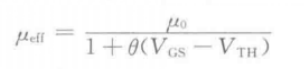
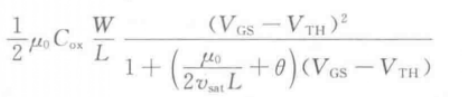 其中
其中晶体管已经发生速度饱和时,如何增大漏极电流
可以通过降低Vds使它不发生速度饱和来增大漏电流吗,答案是不能。因为不发生速度饱和效应和发生速度饱和效应时线性区电流几乎相等,当我们减小Vds时,只会让漏电流减小,而不会因为没发生速度饱和而使电流增大。正确增大漏电流的方法:是增大沟道长度L(并同比例增大W),以使其不发生速度饱和效应。> 参考:-
https://zhuanlan.zhihu.com/p/124315932
- https://blog.csdn.net/qq_50968231/article/details/126312263
倒比管
倒比管就是L>W的mos管。电阻比较大,电流比较小。一般用于低功耗电路中。电流镜的失配mismatch
方法:只有L能改善失配特性,L增加一倍,失配性能能改善一倍1:1电流镜
在之前一直对最简单的电流镜的失配存在一些误解,比如下图中最简单的电流镜,输出电流和输入电流失配应该如何改善?之前的理解认为加大电流镜管子尺寸可以提升精度,但其实真正决定失配精度的是MOS管的Length。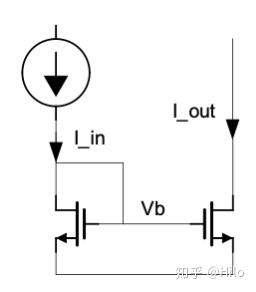
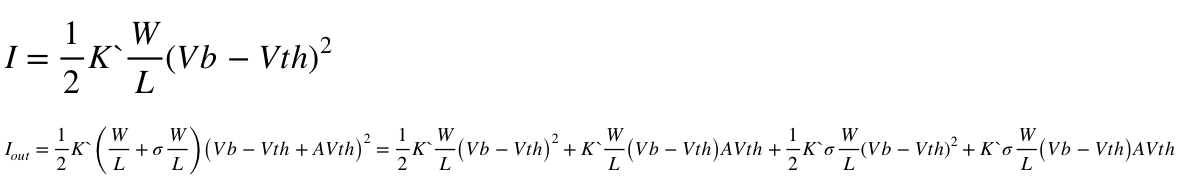 在上面的公式中,忽略了失配的二次项。
在上面的公式中,忽略了失配的二次项。 上一步计算中,同样是忽略了失配的二次项。先看右边部分,L越大,σW越小。W越大,σL就越小。因此
上一步计算中,同样是忽略了失配的二次项。先看右边部分,L越大,σW越小。W越大,σL就越小。因此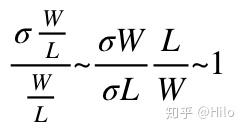 两者刚好抵消,因此对输出电流的失配没有影响。然后观察左边部分,这边会有一个前提,即输出电流是不变的。因此可以将上边的公式转化为:
两者刚好抵消,因此对输出电流的失配没有影响。然后观察左边部分,这边会有一个前提,即输出电流是不变的。因此可以将上边的公式转化为: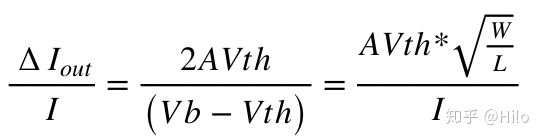 AVth是与MOS管尺寸成反比的。
AVth是与MOS管尺寸成反比的。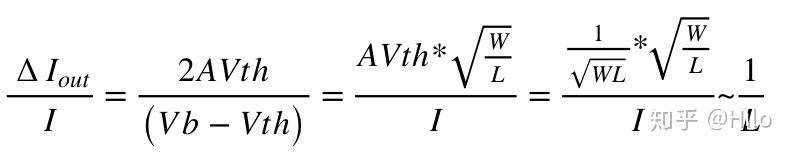 从上边的公式中可以看出,只有L能改善失配特性,L增加一倍,失配性能能改善一倍。仿真结果在cadence上搭建了简单的电流镜电路,用monte-carlo仿真得到输出电流的失配标准差。
从上边的公式中可以看出,只有L能改善失配特性,L增加一倍,失配性能能改善一倍。仿真结果在cadence上搭建了简单的电流镜电路,用monte-carlo仿真得到输出电流的失配标准差。
1:N电流镜
当电流镜MOS管不相等时,如下图所示: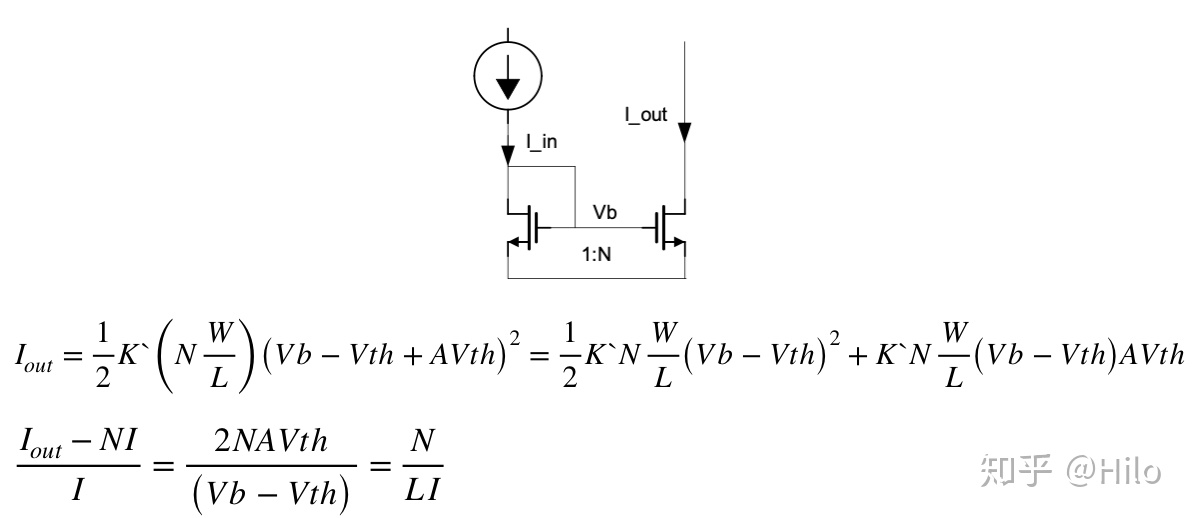 如下的仿真结果也验证了上面的理论分析:
如下的仿真结果也验证了上面的理论分析: 因此,sigma随着电流增加而变大,但是与输出电流的比例是不变的,均是23.5m。Sigma / Iout = 23.5m
因此,sigma随着电流增加而变大,但是与输出电流的比例是不变的,均是23.5m。Sigma / Iout = 23.5m不同输出电流之间的失配
在实际使用的过程中,我们关注的往往不是一路输出电流和被镜像电流之间的关系,而是不同路输出电流之间的匹配关系。如下图所示: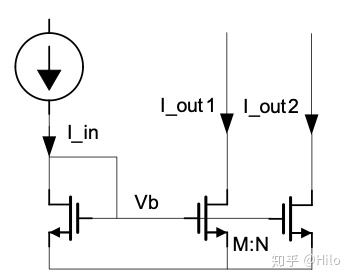 两路输出的MOS管尺寸比为M:N。可以认为两路输出均是互相独立的随机事件,而且由之前的章节可以得到I_out1和I_out2的标准差为Mσ和Nσ。根据概率论的内容,两路输出电流的标准差为:
两路输出的MOS管尺寸比为M:N。可以认为两路输出均是互相独立的随机事件,而且由之前的章节可以得到I_out1和I_out2的标准差为Mσ和Nσ。根据概率论的内容,两路输出电流的标准差为: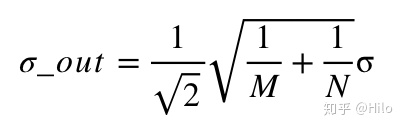 仿真结果:
仿真结果: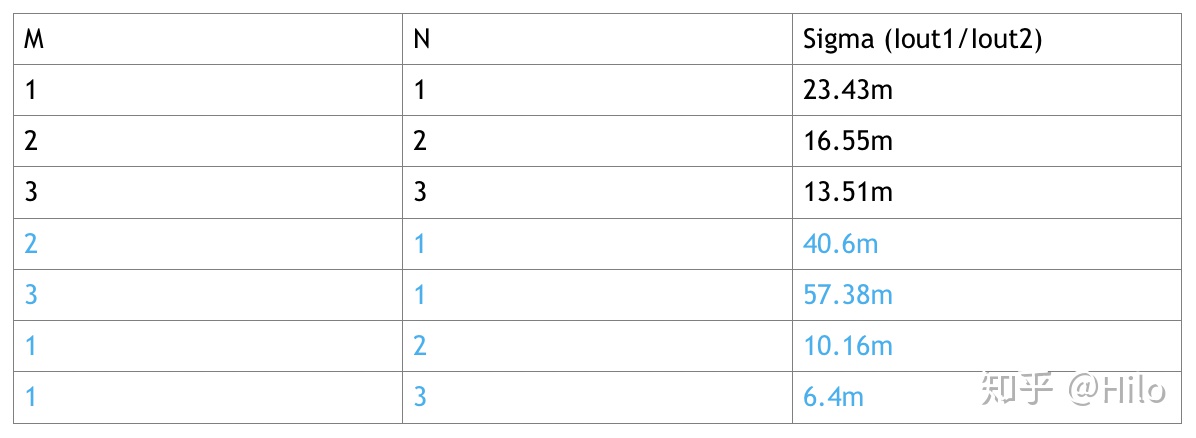 M/N从1/1,2/2,3/3的sigma满足公式。可以看到,M=N=1时,sigma=23.5m。M=N=2时,sigma=1/sqrt(2)*23.5m=16.6m。M=N=3时,sigma=1/sqrt(2)*sqrt(2/3)*23.5=13.56m. 实际仿真结果与理论计算十分符合。当M=1,N=2时,Iout1/Iout2=0.5。理论计算的sigma=1/sqrt(2)*sqrt(3/2)*23.5/2=10.18m。当M=1,N=3时,Iout1/Iout2=1/3。理论计算的sigma=1/sqrt(2)*sqrt(4/3)*23.5/3=6.4m。(这两种情况下,23.5除了实际的电流比例。这是因为23.5m是1:1时的sigma,如果是1/2,那么sigma就会减半。)最后一种情况是M=2,N=1,此时电流比例为2。理论计算的sigma=1/sqrt(2)*sqrt(3/2)*23.5×2=40.72m。也是和仿真结果十分符合的。参考:https://zhuanlan.zhihu.com/p/57865711
M/N从1/1,2/2,3/3的sigma满足公式。可以看到,M=N=1时,sigma=23.5m。M=N=2时,sigma=1/sqrt(2)*23.5m=16.6m。M=N=3时,sigma=1/sqrt(2)*sqrt(2/3)*23.5=13.56m. 实际仿真结果与理论计算十分符合。当M=1,N=2时,Iout1/Iout2=0.5。理论计算的sigma=1/sqrt(2)*sqrt(3/2)*23.5/2=10.18m。当M=1,N=3时,Iout1/Iout2=1/3。理论计算的sigma=1/sqrt(2)*sqrt(4/3)*23.5/3=6.4m。(这两种情况下,23.5除了实际的电流比例。这是因为23.5m是1:1时的sigma,如果是1/2,那么sigma就会减半。)最后一种情况是M=2,N=1,此时电流比例为2。理论计算的sigma=1/sqrt(2)*sqrt(3/2)*23.5×2=40.72m。也是和仿真结果十分符合的。参考:https://zhuanlan.zhihu.com/p/57865711 -



【推荐】国内首个AI IDE,深度理解中文开发场景,立即下载体验Trae
【推荐】编程新体验,更懂你的AI,立即体验豆包MarsCode编程助手
【推荐】抖音旗下AI助手豆包,你的智能百科全书,全免费不限次数
【推荐】轻量又高性能的 SSH 工具 IShell:AI 加持,快人一步
· Manus爆火,是硬核还是营销?
· 终于写完轮子一部分:tcp代理 了,记录一下
· 震惊!C++程序真的从main开始吗?99%的程序员都答错了
· 别再用vector<bool>了!Google高级工程师:这可能是STL最大的设计失误
· 单元测试从入门到精通