Homework3

/**
* Finds and prints n prime integers
* Jeff Offutt, Spring 2003
*/

private static void printPrimes(int n) {
int curPrime; //Value currently considered for primeness
int numPrimes; // Number of primes found so far;
boolean isPrime; //Is curPrime prime?int[] primes = new int[MAXPRIMES];// The list of primes.

// Initialize 2 into the list of primes.
primes[0] = 2;
numPrimes = 1;
curPrime = 2;
while(numPrimes < n) {
curPrime++; // next number to consider...
isPrime = true;
for(int i = 0; i <= numPrimes; i++ ) {
//for each previous prime.
if(isDvisible(primes[i],curPrime)) {
//Found a divisor, curPrime is not prime.
isPrime = false;
break;
}
}
if(isPrime) {
// save it!
primes[numPrimes] = curPrime;
numPrimes++;

}
}// End while

// print all the primes out
for(int i = 0; i < numPrimes; i++) {
System.out.println("Prime: " + primes[i] );

}

}// End printPrimes.

(a) Draw the control flow graph for the printPrime() method.
(b) Consider test cases t1 = (n = 3) and t2 = ( n = 5). Although these tour the same prime paths in printPrime(), they don't necessarily find
the same faults. Design a simple fault that t2 would be more likely to discover than t1 would.
(c) For printPrime(), find a test case such that the corresponding test path visits the edge that connects the beginning of the while statement
to the for statement without going through the body of the while loop.
(d) Enumerate the test requirements for node coverage, edge coverage,and prime path coverage for the path for printPrimes().
(e) List test paths that achieve node coverage but not edge coverage on the graph.
(f) List test paths that achieve edge coverage but not prime path coverage on the graph

 

(a)控制流图如下

 

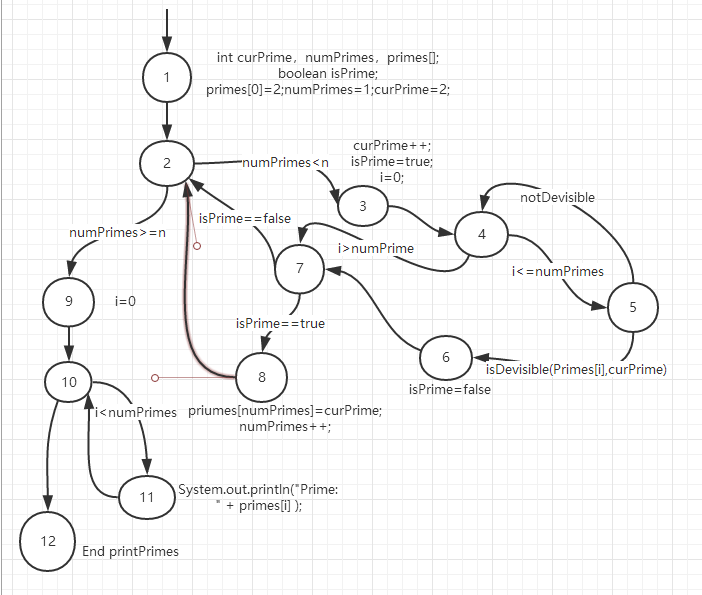
（b）对于数组越界的错误，t2比t1有更高可能发现错误

 

（c）对于经过while节点且不执行while循环体的测试样例，设计t = （n = 1）即可

 

（d）

点覆盖：{1,2,3,4,5,6,7,8,9,10,11,12}

边覆盖：{1,2}，{2,3}，{3,4}，{4,5}，{4,7}，{5,4}，{5,6}，{6,7}，{7,2}，{7,8}，{8,2}，{2,9}，{9,10}，{10,11}

　　　　{11,10}，{10,12}

主路径覆盖：{1,2,3,4,5,6,7,8}，{1,2,9,10,11}，{1,2,9,10,12}，{2,3,4,5,6,7,8,2}，{2,3,4,7,2}，{2,3,4,5,6,7,2}，{4,5,4}，{5,4,5}，{3,4,5,6,7,8,2,9,10,12},{3,4,5,6,7,8,2,9,10,11},{10,11,10},{11,10,11},{11,10,12}

 

（e）点覆盖测试路径：{1,2,3,4,5,6,7,8,2,9,10,11,10,12}

 

（f）边覆盖测试路径：{1,2,3,4,5,4,5,6,7,8,2,9,10,11,10,12}，{1,2,3,4,7,2,9,10,12}；