浅析 PBR/BRDF
浅析 PBR/BRDF
过了几个月之后，还是将文章名改为浅析。什么深入理解，完全看懂。。。开玩笑，完全看不懂好嘛 -_-|||
本文是在上文的基础上进行的增减
实时渲染中的 PBR 方程是这样的
1. L 的单位
1.1 辐亮度是什么
首先，给上一堆光学和照明中常用概念和单位对比，上面文章中给的还不是很清晰。
参考链接：https://www.zhihu.com/question/407170937/answer/1415758129 和 https://www.cnblogs.com/snake553/p/5206545.html 以及ChatGPT。
-
发光强度 Luminous Intensity
- 符号： \(I\) . 国际单位制中，1cd （坎德拉）为一光源在给定方向上的发光强度，该光源发出频率为 \(540 \times 10^{12} \mathrm {Hz}\) 的单色辐射，且在此方向上的辐射强度为 \(1/683 \mathrm{W/ \color{red}{sr}}\) (瓦特每球面度)
-
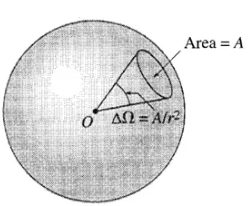
立体角
-
Solid Angle , 符号 ： \(\Omega\)
-
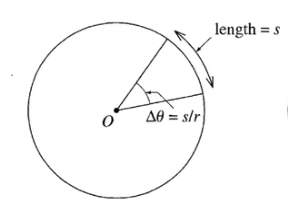
以圆锥体的顶点为球心，半径为 1 的球面被锥面所截得的面积来度量的，度量单位为 "立体弧度 (steradian，缩写为 sr)"。立体弧度，又称为球面弧，可以看作是三维的弧度，是立体角的国际单位。
-
二维角度 \(\Delta\theta=s/r\)
-
三维角度 \(\Delta\Omega=A/r^2\)
\[\mathrm d\Omega=\frac{\mathrm dA}{r^2} \tag{1.1} \]
-
-
-
光通量 Luminous Flux
-
符号： \(\Phi\). 从一光源发射出光的量度。单位是流明 lumen, lm。
\(1 lm\)为发光强度 \(I\) 为 \(1 cd\) 的均匀点光源在 \(1 sr\) 球面度立体角 \(\Omega\) 内发出的光通量 \(\Phi\)。流明一般用来作为钨丝灯与日光灯的量测单位。例如一支 40 W 日光灯管则可产生 2100 lm 的光通量
-
通量
-
通量（flux）是一个广义概念，通常指的是一个矢量场通过一个给定表面的“流量”或“量”。这个概念在物理学、工程学和数学中都有应用。
在物理学中，通量可以表示为一个矢量场通过一个给定表面的流量，比如磁通量、电通量或者光通量。
在数学中，通量可以描述为一个矢量场穿过一个给定曲面的“流动”量。在向量场理论中，通量通常用来描述场的强度或者场的流动情况。通常通过对向量场的法向分量在曲面上的积分来计算。
-
-
-
-
Illuminance 照度
-
符号： \(E\).
-
定义：在给定表面上单位面积接收到的光通量，也就是光源发射出的光能量落在表面上的密度。
评价光照环境质量的参数，通常用于建筑照明设计、摄影、光学工程等多个领域。
单位：\(Lux, lx\) 勒克斯。\(1lx=1lm/1m^2\) ，1 流明的光通量均匀分布在 1 平米面积上的照度为 1 勒克斯
-
公式：
\[E=\Phi/A \tag{1.2} \] -
照度的概念不同于 Luminous Intensity 和 Luminance ，它关注的是光源照射在物体表面后的光能量分布情况，而非光源本身发射光的能力或是物体表面发射光的能力。
-
-
光亮度 Luminance
-
符号 \(L\).
-
定义： 在一个平面上，单位面积在单位立体角内发出或反射的光通量，它是视觉系统能够感知到的一个表面亮度属性。
光亮度主要反映了光源或者物体表面朝向观察者方向的光强密度，是一个方向性和面积相关的物理量。
-
公式
\[L=I/S=\frac{\mathrm d^2{\Phi_v}}{\mathrm dA \cdot \mathrm d\Omega} \tag{1.3} \]- \(L\) 是光亮度
- \(\Phi_v\) 是垂直于表面的单位面积 \(dA\) 上，在单位立体角 \(d\Omega\) 内发出或反射的光通量（光通量的视觉贡献部分）
- \(dA\) 是微小面积
- \(d\Omega\) 是立体角微分
-
单位：Luminance 的国际单位是坎德拉每平方米 \(cd/m^2\)，也称为 尼特 \(nit\)
-
对于一个漫散射面，尽管各个方向的光强和光通量不同，但各个方向的亮度是相等的（后面有证明）。早期电视机的荧光屏就是近似于这样的漫散射面，所以从各个方向上观看的图像都有相同的亮度感。早期黑白电视机荧光屏的亮度在120nits左右
-
| 幅度学符号 | 名称 | 单位 | 对应色度学名称 | 色度学符号 | 色度学单位 |
|---|---|---|---|---|---|
| \(Q\) | Radiant Energy 辐射能 | 焦耳 \(J\) | Luminous Energy 光能量 | \(Q\) | lumen-second 表示光源在一秒内释放的光的总量 |
| \(\Phi_e\) | Radiant flux 幅通量 | 瓦特 \(W\) | Luminous flux 光通量 | \(\Phi_v\) \(v\) 表示 visual，表示光通量是根据人眼对光的感知来定义的 |
流明，lumen，通常表示为 lm |
| \(I\) | Intensity 辐强度 | \(W/sr\) | Luminous Intensity 发光强度/光度 | \(I_v = \Phi_v/\Omega\) | 坎德拉，candela, \(cd=lm/sr\) |
| \(E\) | Irradiance 辐照度 | \(W/m^2\) | Illuminance 照度 | \(E=\Phi_v/A\) | 勒克斯 lx, \(lx=lm/m^2\) |
| \(L\) | Radiance 辐亮度 | \(W/(m^2sr)\) | Lunimance 光亮度 | \(L = I/S=\Phi/(\Omega S)\) | 尼特 \(nit=lm/(m^2sr)=cd/m^2\) |
-
Irradiance 辐照度
-
符号: \(E\)
-
定义：单位时间内 垂直于辐射传播方向上的 单位面积行接收到的辐射能量通量。简单来说，辐照度 irradiance 就是辐射能量落在某个表面上的强度，即 每平方米面积上每秒钟接收到的能量（功率）。
-
公式：
\[E=\Phi_e/A \tag{1.4} \] -
单位：\(W/m^2\)
-
-
Radiance 辐亮度
-
从某一表面或通过某一体积元素，在给定方向上 单位立体角内单位投影面积 和单位波长间隔内的辐射通量。简单来说，辐亮度衡量的是辐射能量沿特定方向传输的密度。
\[L_e(\omega, \bold n) = \frac{\mathrm d^2 \Phi_e}{\mathrm d A^{\scriptstyle{\perp}} \cdot \mathrm d\Omega} = \frac{\mathrm d^2 \Phi_e}{\cos \theta \cdot \mathrm dA \cdot \mathrm d\Omega} \tag{1.5} \] -
这个公式非常重要，是理解一切的基础
-
为什么是 \(\cos \theta\) ，看下图就知道了
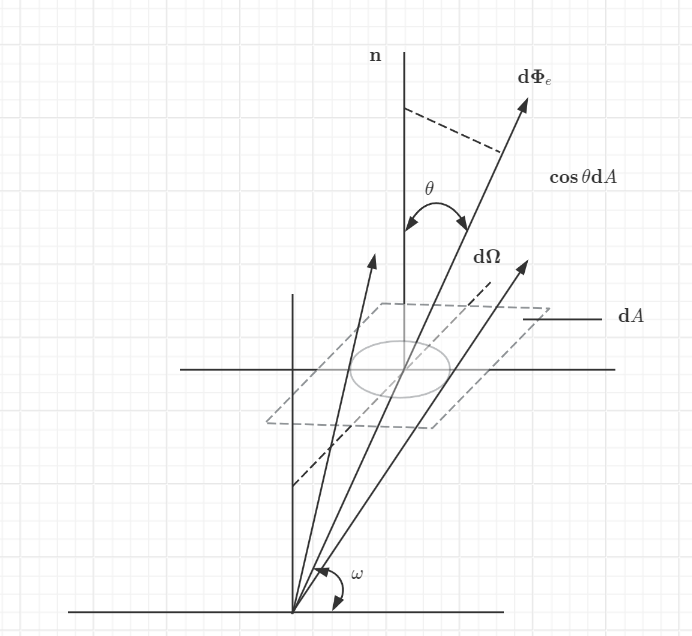
穿过坐标原点的两个平面只是为了说明 \(\cos \theta\)，并不是真正的 \(\mathrm dA\)
- \(L_e\): 辐射亮度，单位 \(W/(m^2sr)\)
- \(\Phi_e\): 通过包含指定点的辐射束截面积 \(\mathrm dA\) 在立体角元 \(\mathrm d\Omega\) 内的幅射通量
- \(\bold n\): 表面法线方向
- \(\omega\) ： 辐射的方向
- \(\theta\) : 辐射方向 \(\omega\) 与 表面法线 \(\bold n\) 之间的角度
- \(\cos \theta\) 用来归一化辐射强度，\(\mathrm dA\cos\theta\) 是辐射束截面积 \(dA\) 在垂直于 辐射角度 \(\omega\) 的平面内的投影面积
-
光亮度不随距离变化的理解
距离变远之后，虽然到达人眼的光通量变小了，但是形成的图像也小了。（理解通量的定义很好理解这个，这里不贴证明了，想要证明的直接看原文）
2. BRDF 到底是什么
首先，根据公式(1.4)
以及公式(1.5)
可以计算下整个半球面上面的辐照度 \(E\)
在数学和物理中，尤其是光学和辐射传输领域，\(\omega\) 通常用来表示三维空间中的方向向量，它可以视为从原点指向一个方向的单位向量。尽管如此，当涉及到辐射强度或辐射亮度随方向变化时，我们确实可以借助 \(\omega\) 来间接表示立体角 \(\Omega\) 的变化，即立体角微分 \(\mathrm d\Omega\)。
在三维空间中，一个完整的立体角 \(\Omega\) 单位是立体弧度（steradian，缩写为 sr），它描述的是一个圆锥（所有射线汇聚于一点形成的立体角）相对于整个球面的面积比例。当我们谈论 dω 时，尽管它不是一个严谨的数学符号，但很多时候被当作是立体角 \(\Omega\) 的微小变化的简写，即 \(\mathrm d\Omega\)。
所以，尽管 \(\omega\) 可以想象为一个二维角度的延伸，但在辐射传输的语境下，它实际上代表的是三维空间中的方向，而 \(\mathrm d\omega\) 被用来直观地表示立体角 \(\Omega\) 的微小增量，其单位仍是立体弧度（sr）。
则辐照度 \(E\) 对 角度 \(\omega_i\) 微分
尽管单位不同，但在表达式 \(\mathrm dE(p, \omega_i) = L_i(p, \omega_i) \cos\theta_i \mathrm d\omega_i\)，这里的 \(\mathrm d\omega_i\) 应该理解为在辐射亮度 \(L_i(p, \omega_i)\) 计算中的立体角微分 \(\mathrm d\Omega\) 的一种简写或符号约定。在物理意义和数值上，它们应当是一致的，尽管严格来说单位并不相同（立体角的单位是sr，而方向向量本身并没有明确的单位）。所以在这里，\(\mathrm d\omega_i\) 更像是借用方向向量符号来表达立体角微分的意思。
2.1 BRDF 定义
以下摘自毛星云《Real-Time Rendering 3rd 提炼总结》以及 《Real-Time Rendering (2018, CRC Press)》
可以将一个表面着色的过程，理解为给定入射的光线数量和方向，计算出指定方向的出射光亮度（radiance，\(L_o\)）。
在 computer graphics 中，BRDF（Bidirectional Reflection Distribution Function，双向反射分布函数）是一个用来描述表面如何反射光线的方程。（这里的双向，是指 入射光方向 和 出射光方向）。
-
精确定义
- 出射辐射率的微分（differential outgoing radiance）和 入射辐照度的微分（differential incoming irradiance） 之比：
\[f(\bold l, \bold v)=\frac{\mathrm dL_o(\bold v)}{\mathrm dE(\bold l)} \tag{2.3} \]\(\bold l\) for incoming light direction
\(\bold v\) for outgoing view direction
Real-Time Rendering 2018, Chapter 9, Section3, The BRDF
\(\bold n\) 和 \(\bold l\) 如下图
-
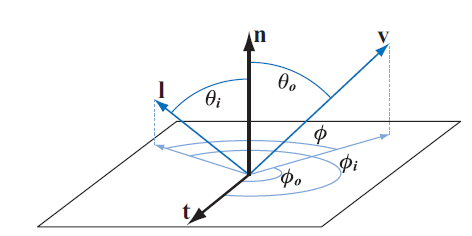
这里解释一下为什么 \(\bold l\) 是这个方向不是反方向？
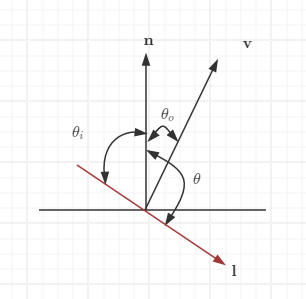
上图中是原有的方向，用 \(\displaystyle \cos \theta = \frac{\bold l \cdot \bold n}{|\bold n||\bold l|}\) 可以得到 \(\theta\) ，但是 \(\theta_i\) 是我们想要的，计算更方便，又 \(\displaystyle \cos \theta_i = \cos (\pi -\theta) = - \frac{\bold l \cdot \bold n}{|\bold n||\bold l|} = \frac{(-\bold l) \cdot \bold n}{|\bold n||\bold l|}\) ，所以直接用 \(-\bold l\) 代替 \(\bold l\)
2.2 为什么用 \(L_o/E\)
因为照射到入射点的不同方向的光，都可能从指定的反射方向出射，所以当考虑入射时，需要对面积进行积分。而辐照度 irradiance 正好表示单位时间内到达单位面积的辐射通量 (\(E=\Phi/A\))。
所以 BRDF 函数选取入射时的辐照度 irradiance \(E\)，和出射时的辐亮度 radiance \(L\)，可以简单明了地描述入射光线经过某个表面反射后如何在各个出射方向上分布。
直观来说，BRDF 的值给定了入射方向和出射方向能量的相对量。
\(E = \Phi/A\) 而 \(L=\displaystyle \frac{\mathrm d^2\Phi}{\cos \theta \mathrm d A \mathrm d\Omega}\) 所以 得 \(\mathrm dE(p, \omega_i)=L_i(p, \omega)\cos \theta_i \mathrm \ d\omega_i\) ，故 BRDF 的单位为 \(sr^{-1}\)
这里毛星云大神的解释没太看懂，以下是 通义千问 的解释：
在图形学和光度学中，BRDF 的这种定义方式确保了其具有以下性质：
-
归一性 Energy Conversation
考虑整个半球上的入射光，散射出去的光能量不会超过入射光能量，即对于所有的出射方向， BRDF 积分必须 <= 1.
\[\int_{\Omega}f_r(\omega_o, \omega_i) \cos\theta_i \ \mathrm d\omega_o \le 1 \tag{2.4} \] -
物理意义
BRDF 描述了光在反射过程中的 能量转换 和 分布规律，将入射光的能量分布转化为出射光的能量分布。因此将其作为出射亮度与入射照度的比率是合理的。
-
方向相关性
BRDF 依赖于入射和出射的方向，因此通过这种方式定义的函数可以捕捉到不同材质表面（如镜面、粗糙表面、各向异性表面等）特有的反射行为。
通义千问给出的公式：
\[f_r(\omega_o, \omega_i) = \frac{\mathrm d L_e(\omega_o)}{\mathrm d E_i(\omega_i)} \tag{2.5} \]
实际上，在某些简化情况下，特别是在一些图形学应用中，可能会省略掉 \(\mathrm dE_i\) 分母上的 \(d\omega_i\)，因为在理想化的假设下（如均匀照明或者微平面近似下），入射照度可以认为是常数，此时 BRDF 可以直接表示为出射辐亮度和入射辐照度的比例。但是严格意义上讲，BRDF 应当提现的是两个方向间亮度微分和照度微分之间的关系。
如果还不懂，看下面的就懂了
为什么不用 \(L_o/L_i\) 或者 \(E_o/E_i\)
-
定义目的
BRDF 旨在描述表面材质如何改变 入射光的方向和能量分布，使其变为出射光。它关注的是在给定入射光条件下，单位面积上单位立体角的出射辐亮度 radiance 与单位面积上的入射辐照度 irradiance 之间的关系，而不是两种亮度或者照度之间的直接比例关系。
这句话我觉得是废话
-
物理意义
入射辐照度 \(E_i\) 是单位面积上接收到的辐射能量通量，而出射辐射亮度 \(L_o\) 是单位面积、单位立体角上发出的辐射能量通量。BRDF 通过 \(L_o/E_i\) 表达了从入射能量转化到出射方向上的效率和分布特点。
这句也是废话，但是上面两句废话还是列在这里，其实帮助重复理解一下 \(E_i\) 和 \(L_o\) 的定义。
-
能量守恒
BRDF 要求满足能量守恒定律，即入射到物体表面的所有辐射能量不能超过反射出的能量。通过 \(L_o/E_i\) 的形式，可以确保在对所有的出射方向进行积分时，总出射能量不会超过入射能量。
用 \(L_o/E_i\) 的形式就能量守恒？用 \(L_o/L_i\) 或者 \(E_o/E_i\) 的形式就可能不遵循能量守恒吗？为什么？
- 能量守恒的考量
- 入射辐照度 \(E_i\) 是单位面积上接收到的辐射能量通量，是 所有入射方向能量的总和
- 能量守恒的考量
最终能让我大概看懂的Why isn't a BRDF a ratio of radiances? - Computer Graphics Stack Exchange
There are a couple of ways to answer this question: an algebraic way and a geometric way.
Algebraically, we can identify this units that the BRDF must have by looking at its place in the rendering equation. The classic rendering equation is:
The output value on the left is a radiance, so the result of the integral must also be a radiance. The integrand contains a radiance multipled by a solid angle \(\mathrm d\omega'\), so something else in the integrand has to cancel out that factor of solid angle. The \(n \cdot \omega'\) factor is dimentionless, and the only other thing is the BRDF--so to make the whole thing work out, the BRDF must have units of inverse solid angle. Equivalently, the BRDF can be seen as a ratio of radiance to irradiance, since they difer by a factor of solid angle in the denominator of radiance.
- integrand 被积函数
- solid angle 立体角
- denominator 分母
Another way to see it is that the BRDF plays a role similar to a probability density. If you look at how probability densities work, they have units inverse to the volume of their domain. For instance, a 1D probability density has units of inverse length (probability per unit length, but probability itself is dimensionless), a 2D one has units of inverse area, and so on. The BRDF acts much like a probability density defined on the hemisphere, giving a likelihood for a photon coming in from a given direction to be reflected into some other direction. So, like any other probability density on a spherical domain, it has units of inverse solid angle.
Geometrically, we can get right down to brass tacks and take apart what's going on in the integral in the rendering equation. Recall that an integral means to subdivide the domain into many tiny pieces and sum the integrand over all the pieces (in the limit as pieces get infinitesimally small). Let's look at one such piece. The integrand should result in an infinitesimal amount of radiance \(\mathrm dL\), since we are going to sum over many pieces to arrive at a finite outgoing radiance. So a single infinitesimal piece of the integral looks like:
- brass tack 基本事实
- infinitesimal a. 无穷小的
- infinitesimally adv. 极小的
If we regroup the factor a bit, the combination \(L_{incoming}(n \cdot \omega') \mathrm d \omega'\) calculates the irradiance on the surface due to the light coming from the infinitesimal solid angle \(\mathrm d\omega'\). Since it's arriving from an infinitesimal amount of solid angle, it produces an infinitesimal irradiance \(\mathrm dE\).
or
So the BRDF acts as a proportionality constant between the infinitesimal irradiance arriving at the surface from an infinitesimal solid angle, and the infinitesimal outgoing radiance generated thereby. It couldn't be a ratio of radiances, because we have a finite incoming radiance, and we need an infinitesimal outgoing radiance if we want to sum up many pieces of the integral and get a finite result. To make that happen, the BRDF would have to be infinitesimal-valued, which ... isn't a thing, in standard mathematics.
所以 BRDF 作为从无限小的立体角到达表面的无限小的辐照度 irradiance 与 由此产生的无限小的出射辐亮度 radiance 之间的比例常量。
3. 菲涅尔反射
3.1 Fresnel 定律
Fresnel 反射描述一个完全平坦的，由两个不同折射率介质组成的表面对光的反射率。
在不同的折射率的介质相交表面，光会部分反射且部分折射，反射的比例就是 Fresnel 系数。Fresnel 系数满足 \(0 \le F_r \le 1\).
已知两种介质的折射率分别是 \(\eta_i\), \(\eta_t\)。根据斯涅尔定律得到折射角和入射角之间的关系：
然后根据推导可以得到平行和垂直偏振光的 Fresnel 反射公式：
此处 标注 一下 Fresnel 定律的推导 菲涅耳公式推导 - 知乎 (zhihu.com)，感兴趣的可以看一下（我只是为了复习下读研时期的电磁场与电磁波知识）
实时渲染中无需考虑偏振光的影响，得到：
解释：
平行 (\(r_{||}\)) 和垂直 (\(r_{\perp}\)) 偏振光的 Fresnel反射率公式分别描述了不同偏振状态的光在从一个介质进入另一个介质时的反射率。在自然光（非偏振光）入射的情况下，我们可以认为入射光是由平行和垂直偏振分量组成的，因此总的反射光强是这两个分量反射光强的叠加。
\(F_r\) 是总反射率（ Fresnel 反射系数的平方），它是平行和垂直偏振分量反射率平方的平均值。这是因为自然光在理想情况下是均匀随机偏振的，所以各偏振态的反射贡献应该按各自概率进行统计平均。对于非偏振光，两种偏振态的能量贡献是相同的，因此总反射率为两种偏振态反射率的算术平均的平方，这样才能保证能量守恒。
而 \(r = E'_{1s}/E_{1s}\) (\(E\) 是电场强度 ) 能量对应 \(E^2\) 所以 \(F_r=(r_{||}^2 + r_\perp^2)/2\)
这是因为在非偏振光照射下，无论光是何种初始偏振状态，均等几率地表现为平行偏振成分和垂直偏振成分，每种成分单独的反射率由对应的Fresnel公式给出，它们各自的平方代表了对应偏振态的能量反射比例，因此取平均值就得到了非偏振光总的能量反射比例。
不同材质的Fresnel系数如图：
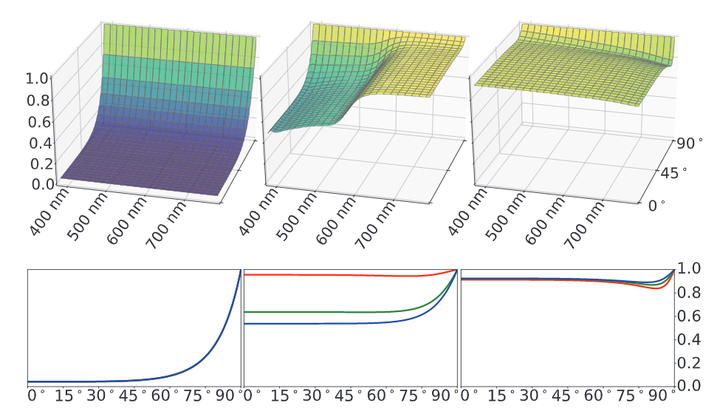
玻璃、铜、铝的Fresnel系数
可以看出在观察角度接近掠夺角（90°）的时候，Fresnel系数都是趋近于 1 的，这种现象叫做Fresnel现象。
接下来要分开讨论电介质和金属：
3.2 电介质
从上图中可以看出，对于电介质（非金属）来说，Fresnel系数基本上不会随着波长变化。
我们现在用 Schlick 来近似表示Fresnel系数：
Christophe Schlick, An Inexpensive BRDF Model for Physically-based Rendering, 1994
将观察角为 0 时的 Fresnel 系数记为 \(F_0\) ，将两种介质的折射率比例记为 \(n\)，得
观察角为 0 则 \(\theta_i=\theta_t = 0\)，代入到 (3.2), (3.3), (3.4) 中计算可得 (3.5)
Schilick 近似为
注意，Schlick 近似不是推导 BRDF 的过程的一部分，反而是先有的 BRDF，后有的 Schlick 近似，可以去看上面的论文。这里只是简单讲述 Schlick 近似
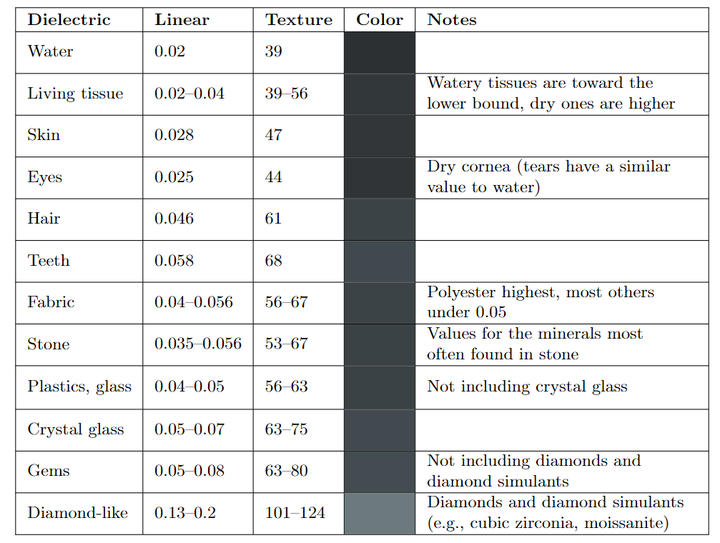
可以看出电介质的 \(F_0\) 一般都很小，在实时渲染中，我们直接取 0.04 作为默认值。
另外需要知道的是，我们这里的 Fresnel 项是 反射的比例，没有被反射的部分自然是形成了折射。因为这里讨论的是不透明表面光，折射部分的光传入介质内部后，部分被吸收，部分再次出射形成漫反射/次表面散射。
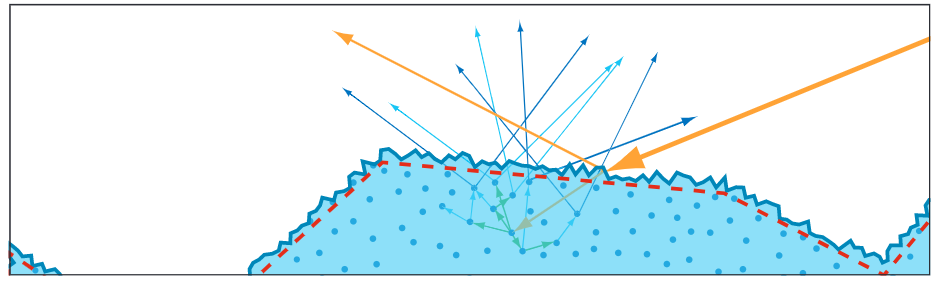
漫反射的形成
3.3 金属
电介质和金属主要区别在于：
3.3.1 金属的折射率是复数
可表示为 \(\bar{\eta} = \eta+ik\) （[参考文献](RefractiveIndex.INFO - Refractive index database))，\(k\) 表示吸收率。
这里菲涅尔公式仍然适用，只是计算起来会复杂一点。
上面我们说电介质的菲涅尔表示反射比例，剩余的部分是折射。对于金属来说，因为金属内部是可以自由运动的电子，其内部自由电子能够在光子作用下集体震荡，形成等效于连续介电层顶的表面电流，这种现象成为表面等离子体共振（Surface Plasmon Resonance, SPR）。这导致金属在可见光以及近红外波段通常具有极高的反射率。根据金属种类、表面状态以及入射光的波长和角度，反射率可以非常高，接近甚至达到100%，尤其是在可见光和近红外波段。
在计算机图形学中，重点通常放在精确模拟金属的镜面反射、高光（specular highlights）以及可能存在的边缘光 （rim lighting）等现象，漫反射成分相比之下总体外观影响较小。
3.3.2 金属的折射率随光波长变化剧烈
因此在 Schlick 近似时，我们要把 \(F_0\) 用 RGB 三个分量来表示，常见的金属 \(F_0\) 值如下所示：
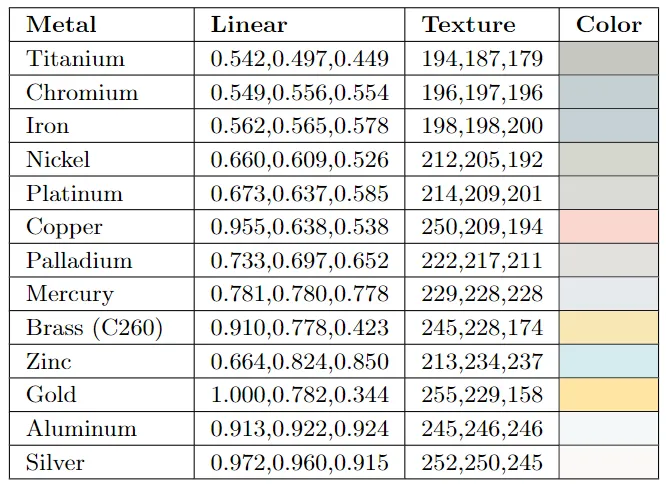
4. BRDF 如何表示全镜面反射
对一个全镜面反射来说，只需要考虑 Fresnel 反射的系数，也就是说
式 (4.1) 的由来：只考虑镜面反射，没有其他漫反射等等，因此只有 \(\omega_r\)
- \(\omega_r\) 是什么？
由式 (0.0) 得：
由 式(4.1) 和 (4.2) 可得：
要知道 BRDF 如何表示全镜面反射，其实就是求解 (4.3) 得到 \(f_r(\omega_o, \omega_i)\)
已知 狄拉克函数 (Dirac delta function, \(\color{red}{\delta(x)}\) ) 有如下性质
式 (4.6) 和 (4.3) 比较，令
代入 \(\displaystyle \int_\Omega f_r(\omega_o, \omega_i)L_i(\omega_i)\cos\theta_i\mathrm d\omega_i\) 得
因此，全镜面反射的 BRDF 为
5. 如何理解漫反射
前面讲过漫反射的成因：没有被菲涅尔反射的部分再次出射形成的。
通常用 Lambertian Model 来描述漫反射。
5.1 Lambertian Reflectance
以下摘自 Lambertian reflectance - Wikipedia
Lambertian reflectance is the property that defines an ideal "matte" or diffusely reflecting surface. The apparent brightness of a Lambertian surface to an observer is the same regardless of the observer's angle of view. More precisely, the reflected radiant intensity obeys Lambert's cosine law, which makes the reflected radiance the same in all directions.
- Examples
- Unfinished wood exhibits roughly Lambertian reflectance, but wood finished with a glossy coat of polyurethane(聚氨酯) does not, since the glossy coating creates specular highlights. Though not all rough surfaces are Lambertian, this is often a good approximation, and is frequently used when the characteristics of the surface are unknown.
Use in computer graphics
In computer graphics, Lambertian reflection is often used as a model for diffuse reflection. This techneque causes all closed polygons (such as a triangle within a 3D mesh) to reflect light equally in all directions when rendered. The reflection decreases when the surface is tilted away from being perpendicular to the light source, however, because the area is illuminated by a smaller fraction of the incident radiation.
The reflection is calculated by taking the dot product of the surface's unit normal vector, \(\vec{N}\), and a normalized light-direction vector \(\vec{L}\), pointing from the surface to the light source. This number is then multiplied by the color of the surface and the intensity of the light hitting the surface:
- \(B_D\)
- brightness of the diffusely reflected light
- \(C\) color
- \(I_L\) intensity of the cincoming light
Because $\vec{L} \cdot \vec{N} = \cos\alpha $ where \(\alpha\) is the angle between the directions of the two vectors, the brightness will be highest if the surface is perpendicular to the light vector, and lowest if the light vector intersects the surface at a grazing angle.
- tilted
- adj. 倾斜的
简单来说，表面法线为 \(\vec{N}\) (归一化矢量), 入射光线归一化矢量 \(\vec{L}\) 与表面法线的夹角为 \(\alpha\)，$\vec{L} \cdot \vec{N} = \cos\alpha $
5.2 Lambertian Model
PBR Step by Step（四）Lambertian反射模型
上面这个链接讲的挺好，和 知乎- 彻底看懂 PBR/BRDF 这里讲的大差不差
这里主要融合这两篇
在 Lambertian 漫反射模型下，由能量守恒知 (\(c\) 是反照率或者固有色，是光在介质内部出射部分的比例， \(1-c\) 表示被介质吸收的比例)
PBR Step by Step（四）Lambertian反射模型 这篇文章中提到了
反射率
又因为，在整个 Lambertian 表面半球积分中 (\(\Omega_o = 2\pi\)) 中，出射通量
式中的 \(\displaystyle \int_{2\pi} \cos \theta_o \mathrm d\omega_o = \pi\) 推导如下
复习下球面积分，看 Triple Integrals in Spherical Coordinates（球坐标中的三重积分） - 知乎 (zhihu.com)
简单来讲，看这张图
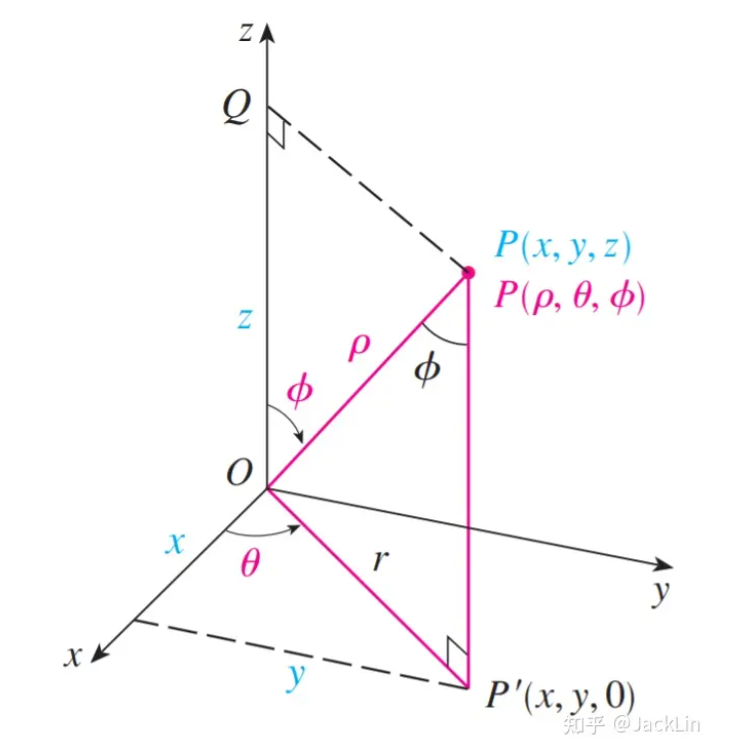
和这张图就能大致回忆起来了
- \(r = \rho \sin\phi\)
- $x=r\cos\theta = \rho\sin\phi\cos\theta $
- $y=r\sin\theta = \rho\sin\phi\sin\theta $
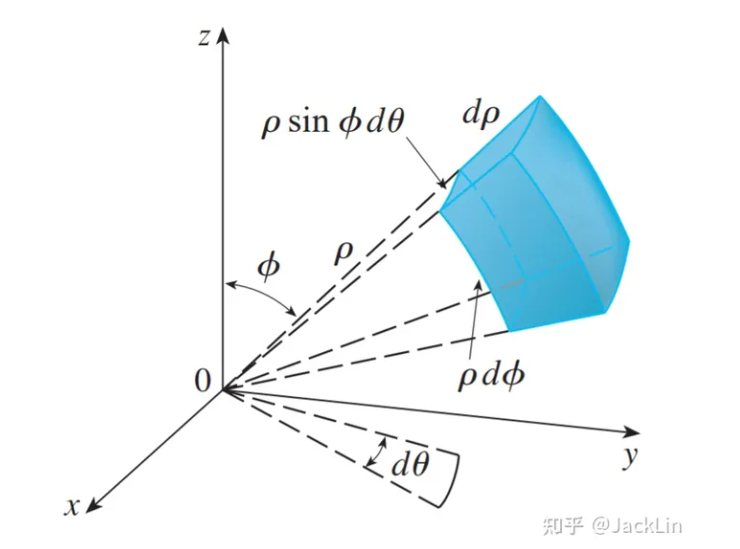
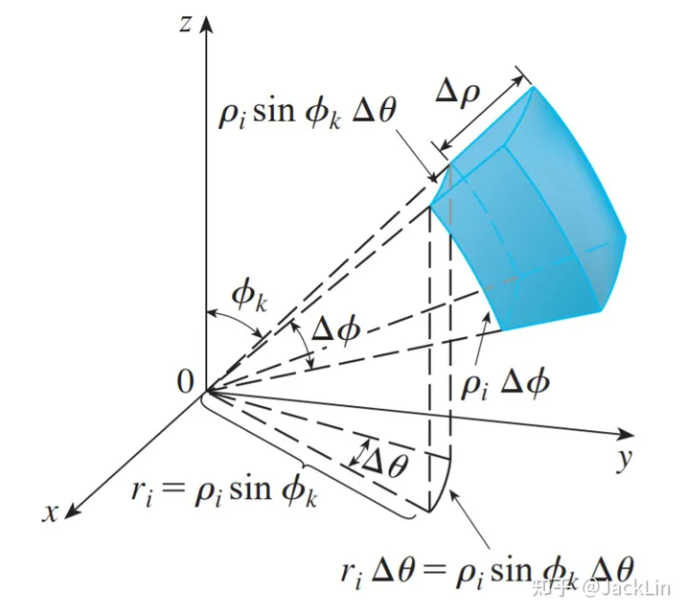
故
\[\int\int\int_E f(x,y,z)\mathrm dV = \int_a^b \int_\alpha^\beta \int_\gamma^\delta f(\rho\sin\phi\cos\theta, \rho\sin\phi\cos\theta, \rho\cos\phi) \color{red}{\rho^2\sin\phi} {\mathrm d\rho \mathrm d\phi \mathrm d\theta} \]
接下来计算半球积分
半球积分值来自于立体角的定义和半球的几何特性。立体角前面讲解过了，就是球面上由该角截取的面积 S 与半径平方 \(r^2\) 的比值。单位球面 r=1 则整个表面积为 \(4\pi\)，对应的立体角为 \(4\pi \ sr\)；半球面为 \(2\pi \ sr\)
数学验证
数学上，立体角元素 \(d\omega\) 可以表示为：
\[\mathrm d\omega = \sin \theta \mathrm d\theta \mathrm d\phi \]注意，这里的 \(\theta\) 和 \(\phi\) 互换了，这里 \(\theta\) 表示从法线方向（顶点）到所考虑点的方位角，取值范围为 \([0, \pi/2]\)；\(\phi\) 是环绕法线方向的方位角，取值范围为 \([0, 2\pi]。\)。（大多数情况下不说明的时候，都是这么表示的，和上面的图中相反）。下面计算仍然使用上图中的说明
也就是 \(\displaystyle \int_{2\pi} \cos \theta_o \mathrm d\omega_o\) 这里的 \(\theta_o\) 实际上应该写为 \(\phi_o\)
\[\begin{aligned} \int_{2\pi} \cos\phi_o d\omega_o &= \int _0^{2\pi} \ \mathrm d\theta \int_0^{\pi/2} \cos\phi \sin \phi \ \mathrm d\phi \\ &= 2\pi * \frac{\cos{2\phi}}{4}|_{\pi /2}^0 = \pi/2 * (1-(-1)) = \pi \end{aligned} \]
入射通量
- 反射率 \(\color{red}{\rho_d}\)
这样，我们就得到了 Lambertian BRDF:
这里 \(\rho_d\) 可以用常数项表示，\(\rho_d = k_dc_d\)
- 漫反射系数 \(k_d\), \(k_d \in [0, 1]\)
- 漫反射颜色 \(c_d\)
Lambertian BRDF 又可以写为：
另一种解释：
Lambertian 漫反射假设在所有方向上观察亮度都是相同的，因此 漫反射的 BRDF 中 \(f_r\) 和 \(\omega_i, \omega'\) 是无关的，是一个常数（\(f_r(p, \omega_o, \omega_i)\) 与 \(\omega_i\) 和 \(\omega_o\) 无关，则变成 \(f_r(p)\)），将 \(f_r\) 提到外面得
故
前面说过 BRDF 的作用之一就是将辐照度 \(E\) 转换为辐亮度 \(L\) ，这里的 \(\displaystyle \frac{1}{\pi}\) 也可以看做是一个用来实现转换的系数。
现实生活中的漫反射并不是完全符合 Lambertian 漫反射模型的，Oren–Nayar reflectance model 模型等一些更加复杂的模型可以更好地表示现实中的漫反射。但是在实际渲染中，使用更加复杂的模型的提升很小。出于性能考虑，目前在实时渲染中 Lambertian 模型还是主流。
6. 微表面模型镜面反射
参考文献：Microfacet Models (pbr-book.org)
未完待续。。。
