透视投影矩阵的推导

透视投影矩阵的推导

本文完全 copy 自 透视投影矩阵的推导 - bluebean - 博客园 (cnblogs.com)

只是用 markdown 将公式全部又打了一遍

图1： View Frustum

Perspective Projection Matrix 的任务就是把位于视锥体内的物体的顶点 (x, y, z) 坐标映射到 [-1, 1] 范围。（如果是 DX 可能是 [0, 1] 范围？）

这相当于把这个四棱台扭曲变形成为一个立方体。这个立方体叫做 规则观察体 (Canonical View Volume, CVV)。如下图

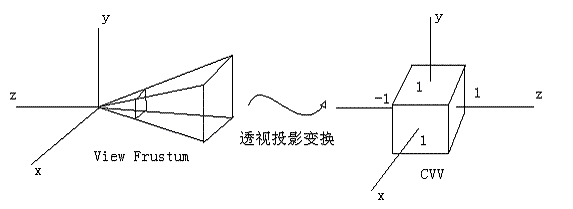
图2 透视投影变换

变换方法或规则

如下图，有一点 \(P\)，位于视椎体内，设坐标为 \((x, y, z)\)。分别对 x, y 坐标和 z 坐标变换到 [-1, 1] 的方式进行讨论

1. x, y 坐标的变换方式

1. 连接视点 eye 与 \(P\) 点与 NearClipPlane 交于 \(P'\) 点
2. 设 NearClipPlane 的宽度为 \(W\)， 高度为 \(H\), \(P'\) 点的 x 坐标范围是 \([-W/2, \ W/2]\)，y 坐标范围为 \([-H/2, \ H/2]\)，然后分别映射至 [-1, 1] 内即可。

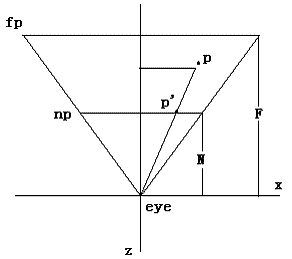
图3 x, y 坐标的变换方式

2. z 坐标的变换方式

z 坐标的范围是 N 至 F，需要映射到 [-1, 1]。映射方法暂时按下不表。

透视投影函数形式

void Matrix4X4::initPersProjMatrix(float FOV, const float aspect, float zNear, float zFar)

• FOV

  • 纵向的视角大小

    

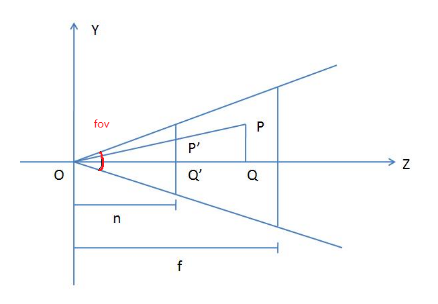
    图4 透视投影函数参数说明

• aspect

  • 裁剪面的宽高比

• zNear

  • NearClipPlane 离 camera 的距离，图 4 中的 n

• zFar

  • FarClipPlane 离 camera 的距离，图 4 中的 f

计算 P 的投影 P‘ 的归一化 P''

通过这几个参数和三角函数可得 near clip plane 的高度：

\[\tan(FOV/2) = \frac{H/2}{zNear} \tag{1} \]

推出

\[H = 2zNear \cdot \tan(FOV/2) \tag{2} \]

因为 \(aspect = W/H\)，故

\[W = 2aspect \cdot zNear \cdot tan(FOV/2) \tag{3} \]

根据相似三角形

\[\frac{zNear}{z} = \frac{y'}{y} = \frac{x'}{x} \tag{4} \]

求得 点 \(P\) 在 near clip plane 的投影点 \(P'\) 的坐标

\[x' = \frac {x \cdot zNear}{z} \ , x \in[-W/2, W/2] \tag{5} \]

\[y' = \frac {y \cdot zNear}{z} , \ y \in[-H/2, H/2] \tag{6} \]

\(x\), \(y\) 的范围沿原点对称，只要将它们分别除以 \(W/2\), \(H/2\) ，就可以使其范围位于 [-1, 1] 内。将 式(2), (3) 代入式 (5), (6)，得

\[x'' = \frac{x'}{W/2} = \frac{2x \cdot zNear}{z\cdot 2aspect \cdot zNear \cdot \tan(FOV/2)} = \frac{x}{z \cdot aspect \cdot \tan(FOV/2)} \tag{7} \]

\[y'' = \frac{y'}{H/2} = \frac{2y \cdot zNear}{z\cdot 2 \cdot zNear \cdot \tan(FOV/2)} = \frac{y}{z \cdot \tan(FOV/2)} \tag{8} \]

假设 \(z \in [-1, 1]\)，则最后需要的点 \(P''\) 为

\[P'' = (\frac{x}{z \cdot aspect \cdot \tan(FOV/2)}, \frac{y}{z \cdot \tan(FOV/2)}, z'') \tag{9} \]

推导矩阵

寻找一个矩阵使得

\[\begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ m_{30} & m_{31} & m_{32} & m_{33} \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{x}{z\cdot aspect \cdot \tan(FOV/2)} \\ \displaystyle \frac{y}{z \cdot \tan(FOV/2)} \\ z'' \\ 1 \end{bmatrix} \]

我们发现求解

\[m_{00}x + m_{01}y + m_{02}z + m_{03}= \frac{x}{z \cdot aspect \cdot \tan(FOV/2)} \]

很难找到合适的 \(m_{00}, m{02}\)，因为坐标 x 和 z 是以加法的形式相邻，右边 z 却成为了 x 的分母。

解决方法：

将右边以四维列向量表示的坐标每一项乘以 z ，有：

\[\begin{bmatrix} m_{00} & m_{01} & m_{02} & m_{03} \\ m_{10} & m_{11} & m_{12} & m_{13} \\ m_{20} & m_{21} & m_{22} & m_{23} \\ m_{30} & m_{31} & m_{32} & m_{33} \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ z \\ 1 \end{bmatrix} = \begin{bmatrix} \displaystyle \frac{x}{aspect \cdot \tan(FOV/2)} \\ \displaystyle \frac{y}{\tan(FOV/2)} \\ z'' \cdot z \\ z \end{bmatrix} \]

因此可得矩阵为

\[\begin{bmatrix} \displaystyle \frac{1}{aspect \cdot \tan(FOV/2)} & 0 & 0 & 0 \\ 0 & \displaystyle\frac{1}{\tan(FOV/2)} & 0 & 0 \\ 0 & 0 & m_{22} & m_{23} \\ 0 & 0 & 1 & 0 \\ \end{bmatrix} \]

第三行第一列

\[m_{22}z + m_{23} = z \cdot z'' \\ \Rightarrow z'' = m_{22} + m_{23}/z \]

又因为 \(z = zNear\) 时，\(z''=-1\)

\(z= zFar\) 时，\(z'' = 1\)
故

\[m_{22} + m_{23}/zNear = -1\\ m_{22} + m_{23}/zFar = 1 \]

联立求得

\[m_{22} = \frac{-zFar-zNear}{zNear-zFar} \\ m_{23} = \frac{2 \cdot zNear \cdot zFar}{zNear - zFar} \]

又 \(1/\tan(FOV/2) = cot(FOV/2)\)，故 投影矩阵为

\[\begin{bmatrix} \displaystyle \frac {\cot(FOV/2)}{aspect} & 0 & 0 & 0 \\ 0 & \cot(FOV/2) & 0 & 0 \\ 0 & 0 & \displaystyle\frac{-zFar-zNear}{zNear-zFar} & \displaystyle\frac{2 \cdot zFar \cdot zNear}{zNear-zFar} \\ 0 & 0 & 1 & 0 \end{bmatrix} \]

将这样的矩阵乘以视锥体中的一个顶点坐标，得到一个新的向量，再将这个向量的每个分量除以第四个分量 \(w\) （这一步叫做透视除法，在 GPU 渲染管线中位于 VertexShader 处理之后，由硬件自动完成），之后就得到了 规则立方观察体中的新坐标。

ZBuffer 中的深度值 DepthValue

z 坐标的映射方式的获得，最后我们是为了方便矩阵乘法的操作，反向求得了 z 坐标与 CVV 中的 z 坐标的映射方式：

\[m_{22} + m_{23}/z = z'' \]

可见两者的映射并不是线性的，如下图所示

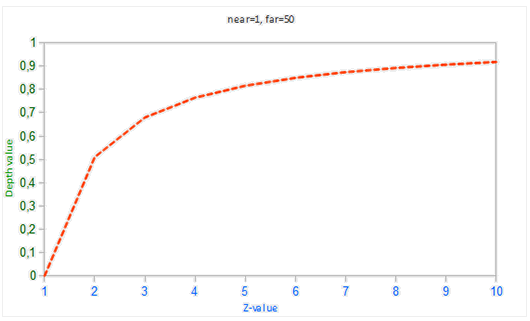
上图为 深度缓存中的深度值 DepthValue 和 物体距离摄像机深度 ZValue 的关系图，其中 \(DepthValue = \displaystyle \frac{z'' + 1}{2}\)，将深度值从范围 [-1, 1] 转换到 [0,1]

代码示例

void Matrix4X4::initPersProjMatrix(float FOV, const float aspect, float zNear, float zFar)
{
    const float zRange = zNear - zFar;
    const float tanHalfFOV = tanf(ToRadian(FOV / 2.0f));
    
    elements[0][0] = 1.0f / (tanHalfFOV * aspect);
    elements[0][1] = 0.0f;
    elements[0][2] = 0.0f;
    elements[0][3] = 0.0f;
    
    elements[1][0] = 0.0f;
    elements[1][1] = 1.0f / tanHalfFOV;
    elements[1][2] = 0.0f;
    elements[1][3] = 0.0f;
    
    elements[2][0] = 0.0f;
    elements[2][1] = 0.0f;
    elements[2][2] = (-zNear - zFar) / zRange;
    elements[2][3] = (2.0f * zNear * zFar) / zRange;

    elements[3][0] = 0.0f;
    elements[3][1] = 0.0f;
    elements[3][2] = 1.0f;
    elements[3][3] = 0.0f;
}

本文是完全 copy 自 透视投影矩阵的推导 - bluebean - 博客园 (cnblogs.com)