制作一个bezier曲线插值器

好玩的东东来啦

最近需要制作一个粒子效果编辑器，界面做得特别烦，但其它比较想做一下那些曲线相关的东西。仅是因为好玩，想学东西

思考：

二阶bezier有一个控制点，能通过该点任意改变两端的斜率，但两个必须联动，因此满足一端时，另一端难以满足；

三阶bezier有两个控制点，能通过这两个控制点任意调节两个端的斜率，因此三阶bezier可以完成任务。干吧！

 

查了一些资料：

 

使用贝塞尔曲线绘制多点连接曲线 讲解的很仔细，能实现不错的效果

Draw smooth curves through a set of points in iOS 讲解的也非常仔细

原文链接：

https://blog.csdn.net/u014084081/article/details/79798231

 

先回顾一下bezier的定义吧

 

 

 

 

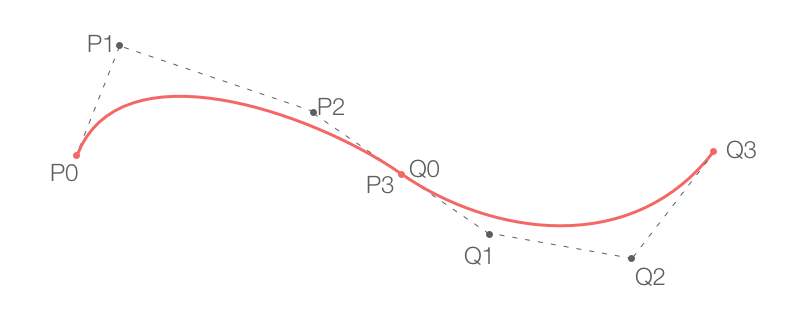
三次方贝塞尔曲线公式如下：

 

 

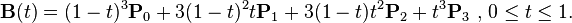
• P0与P3表示曲线的端点，P1, P2表示控制点

上面的公式也可以写作：

 

 

Eq. 01

 

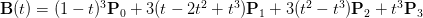
求某一点的斜率，就是对其求导，结果如下：

 

 

Eq. 02

 

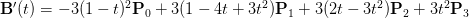
对于第i段，其开始点的斜率应等于第i-1段其结束点的斜率，即：

 

 

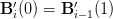
带入t=0和t=1，可得：

 

 

Eq. 03

 

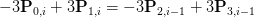
由于片段是连续的，所以：

 

 

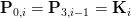
Ki表示的是第i个点

带入Ki后，得到如下的结果：

 

 

Eq. 04

 

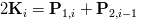
n阶的贝塞尔曲线的导数是是一个n-1阶的贝塞尔曲线，对三阶贝塞尔曲线再求导，得如下的结果：

 

 

Eq. 05

 

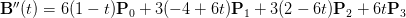
三阶贝塞尔曲线再求导后，其也是连续的，所以，考虑开始点和结束点：

 

 

Eq. 06

 

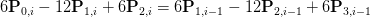
由于P0,i等于P3,i-1（条件1），所以：

 

 

Eq. 07

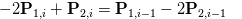
注：bezier一般参数公式：

给定点P0、P1、…、Pn，其贝塞尔曲线即：

 

 

公式说明

1.开始于P0并结束于Pn的曲线，即所谓的端点插值法属性。

2.曲线是直线的充分必要条件是所有的控制点都位在曲线上。同样的，贝塞尔曲线是直线的充分必要条件是控制点共线。

3.曲线的起始点（结束点）相切于贝塞尔多边形的第一节（最后一节）。

4.一条曲线可在任意点切割成两条或任意多条子曲线，每一条子曲线仍是贝塞尔曲线。

5.一些看似简单的曲线（如圆）无法以贝塞尔曲线精确的描述，或分段成贝塞尔曲线（虽然当每个内部控制点对单位圆上的外部控制点水平或垂直的的距离为时，分成四段的贝兹曲线，可以小于千分之一的最大半径误差近似于圆）。

6.位于固定偏移量的曲线（来自给定的贝塞尔曲线），又称作偏移曲线（假平行于原来的曲线，如两条铁轨之间的偏移）无法以贝兹曲线精确的形成（某些琐屑实例除外）。无论如何，现存的启发法通常可为实际用途中给出近似值