计算机浮点数的表示和运算
计算机浮点数和存储和运算规则
1、概述:
众所周知,计算机只能识别二进制数据,即所有的十进制都需要转换成二进制才能在计算机中进行存储和运算,但是,十进制数有整数部分和小数部分,对于整数部分转换成二进制数的话,我们采用除2取余数法;小数部分的话我们采用乘2取整法;求出来后,我们对数字进行规范化处理;
2、来个例子:
把十进制小数6.36转换成二进制,具体怎么操作?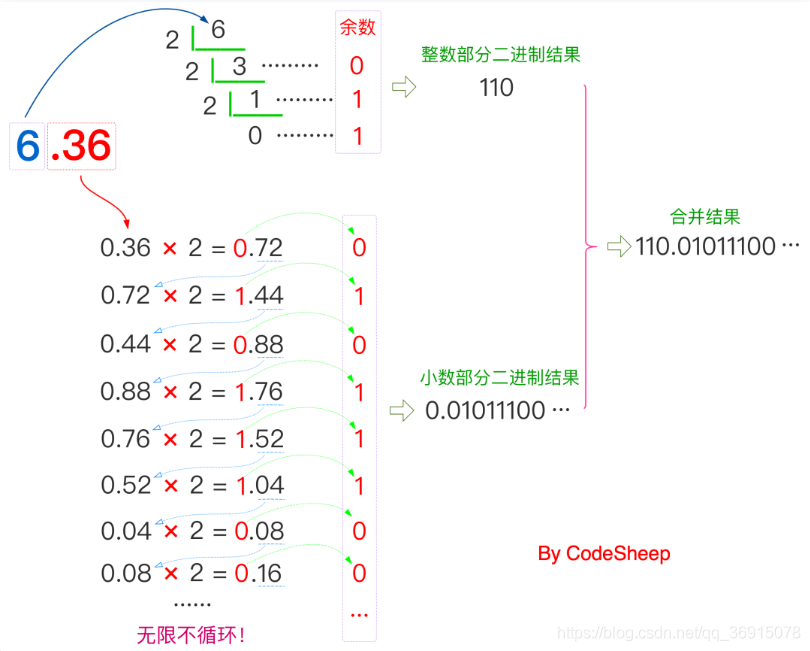
上述例子我们把一个带小数的的十进制转换成了二进制:但是有没有发现一个问题?就是小数部分是一个无限循环的,我们计算机一个存储单元可是存不下这么多数据的呀,虽然可以跨存储区,但是无限的二进制,计算机是存不下的,不可能你定义一个数,结果电脑内存或硬盘立马塞满导致死机吧?那怎么办呢?进行规范化处理
3、规范化处理
规范化处理是只将一个浮点数转换成二进制后,根据存储规则,通过符号位+阶码+尾数的形式表示该浮点数;
data = (-1)^s*M*2*E
在Java语言中,存储浮点数主要有两种基本数据类型:Float和Double
Float:通过Float定义的变量,占4个字节的存储空间,即二进制数的长度为32位
Double:通过Double定义的变量,占8个字节的存储空间,即二进制数的长度位64位

注意:计算机表示浮点数时,是用8位或者11位去存储指数部分,在8位指数位数值上面,表示0~255,但是我们同样需要有负指数,正负指数的位数量为了均等,各自一半,-127~128,0是特殊点,特殊处理。储存时候会加上127,这样就刚刚好是0~255;如果 E 为 11 位,它的取值范围为 0~2047,中间数为1023;这样就能很好的储存了,不然的话,需要判断符号位来判断数值的正负,如下图32位的长度表示浮点数时,我们可以得知当E+127>127则代表该数的阶码为正的,如果E+127<127则代表该数的阶码为负的,即01111111为正负数阶码的分隔值。

4、浮点数的计算
不管任何一门计算机语言,在进行浮点数的计算时都会出现精度问题,下面来看一下Java和JS语言计算浮点数案例:
public class test { public static void main(String[] args) { System.out.println(2.0F-1.5F); System.out.println(2.0F-1.3F); } } 执行结果: 0.5 0.70000005

结论:
我们可以看到,执行结果和我们预期的十进制的计算结果不一样,让我来分析一下:在这里需要大家有点原码/反码/补码的知识;因为计算机不能像十进制一样识别减法操作,所以任何减法都要转换成补码后再相加,比如:A-B = [A]补+[-B]补,正数的原码反码补码都一样:
2.0F - 1.5F
十进制:2.0F 二进制:10.0 规范化:我们在此忽略符号位
原码:1.0000 0000 0000 0000 0000 000*2^1 //因为我们定义变量是Float类型,有效数据位为23位,所以需要补零让长度为23
补码:1.0000 0000 0000 0000 0000 000*2^1
十进制:1.5F
二进制:1.1
规范化:
原码:1.1000 0000 0000 0000 0000 000*2^0 反码:0.0111 1111 1111 1111 1111 111*2^0 //符号位不变,按位取反
补码:0.1000 0000 0000 0000 0000 000*2^0 //补码+1
计算:低阶向高阶看齐,即让2^0向2^1看齐,小数点左移一位则乘以2^1; 01.00000000000000000000000*2^1 + 11.01000000000000000000000*2^1
——————————————————————————————————————
00.01000000000000000000000*2^1 //左边第一个1为符号位溢出去除
所以2.0F-1.5F结果: 0.01000000000000000000000*2^1 = 0.10000000000000000000000*2^0
0.5F的浮点数表示:0.01000000000000000000000*2^0
所以2.0F-1.5F = 0.5F
惊不惊喜?意不意外?那为何2.0F-1.3F会不正确呢?
————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————————
采用相同的分析方法:
2.0F - 1.3F
十进制:2.0F
二进制:10.0
规范化:1.00000000000000000000000*2^1
十进制:1.3F
二进制:1.0100 1100 1100 1100 1100 11001
规范化:1.0100 1100 1100 1100 1100 110*2^0 (23位)
计算:
1.00000000000000000000000*2^1
- 0.10100110011001100110011*2^1 //这里补码我就不求了,操作和上面求补码一样
——————————————————————————————————————————————————————————————————————————————————————
0.01011001100110011001101*2^1
对结果进行规范化:
1.01100110011001100110100*2^-1
0.7的表示:
二进制:0.101110011001100110011001100 (规范化处理时存在一个细节:0舍1入),因为是Float类型,所以规范化处理后,要保留23个有效位即小数点后要有23个数据,但是第24是1所以要往前+1;如果是0则直接舍去;
规范化:1.011100110011001100110011*2^-1
所以最终结果并不相等
5、Java中如何对浮点数进行计算?
通过以上的案例分析,我们发现浮点数计算会存在误差,比如我们去银行里面取钱,我们账户上有2块钱,我们取出来1.3,如果直接通过浮点数进行计算,则我们账户还剩余0.70000005;那这个银行可能就在不知不觉中破产了,所有的程序员和工程师拉去坐牢去.......
那该怎么解决呢?
Java 提供了一个类对浮点数进行精准运算,BigDecimal对象,该类定义了很多可靠的方法,比如计算浮点数时向上取整或者向下取整,保留有效位数等等:
public class test { public static void main(String[] args) { BigDecimal BD1 = new BigDecimal("2.0"); BigDecimal BD2 = new BigDecimal("1.4"); System.out.println(BD1.subtract(BD2)); } } 运行结果: 0.6


 浙公网安备 33010602011771号
浙公网安备 33010602011771号