小白懂算法之二分查找
最近重头刷各种算法,发现自己遗忘了好多;赶紧刷了几道来巩固下记忆,也顺便简单做一个分享,希望能帮到一些小伙伴吧!
一.简介
二分查找是一种查找元素效率特别高的查找算法,也称“折半算法”。
二.前提
二分查找最重要的一个前提条件是 要查找的集合或者序列 必须是 有序的
三.查找的流程
二分查找的流程:
1).确定一个查找值
2).找出序列里面中间的值
3).比较查找值和中间值,两种结果:
》相同,值找到了
》不相同,缩小1/2的的范围,重复2).3)的步骤
四.图解(图片来源百度)
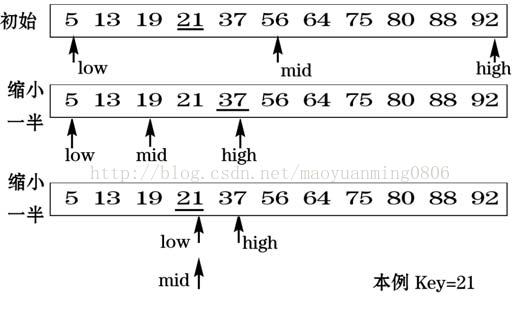
五.代码实现
天上飞的理念,终归得有地上的实现。不然就是在吹水了,语言的话使用Java来实现,这里采用两种方式:递归和while循环。
递归实现二分查找
/** * 使用递归实现二分查找 * @param sortedArr:查找的有序数组 * @param key:查找值,现在目前大多人都叫做关键字,用key表示 * @param low:起点 * @param high:终点 * @return */ public static boolean binarySearchByRecursion(int[] sortedArr, int key, int low, int high) { /** * 校验: * 1.如果 key > sortedArr[high],该值肯定找不到 * 2.如果 key < sortedArr[low],该值肯定找不到 * 3.如果low > high,逻辑不成立,不存在中间值。 */ if(key < sortedArr[low] || key > sortedArr[high] || low > high) { return false; } /** * 得到中间值的下标,有两种结果: * 1.奇数。java默认是向下取整的,取奇数作为中间索引没毛病 * 2.偶数。可取偶数 或者 偶数+1 都行。这里直接取偶数 */ int mid = (high+low)/2; //得到中间值的下标 /* * 判断查找值和中间值 * 1. 查找值 > 中间值,起点向右缩小范围,递归调用本方法 * 2.查找值 < 中间值,终点向左缩小范围,递归调用本方法 * 3.查找值 = 中间值,值找到 */ if(key == sortedArr[mid]) { //查找值 = 中间值 return true; //返回true }else if(key > sortedArr[mid]) { //查找值 > 中间值 //起点缩小范围 low = mid + 1; //递归调用本函数 return binarySearchByRecursion(sortedArr,key,low,high); }else if(key < sortedArr[mid]){ //查找值 < 中间值 //终点缩小范围 high = mid - 1; //递归调用本函数 return binarySearchByRecursion(sortedArr,key,low,high); } return false; }
main方法测试:
public static void main(String[] args) { //准备一个有序数组 int[] sortedArr = new int[] {1,2,3,4,5,6,7,8,9,10,11,12,13,14}; //准备一个查找值 int key = 2; //准备起点位置和终点位置 int low = 0; int high = sortedArr.length-1; //调用二分查找方法返回一个布尔标识符,true - 代表找到,false代表找不到 boolean result = binarySearchByRecursion(sortedArr,key,low,high); //打印结果 if(result) { System.out.println("序列中存在"+key); }else { System.out.println("序列中不存在"+key); } }
while实现二分查找
public static boolean binarySearchByWhile(int[] sortedArr, int key, int low, int high) { /** * 校验: * 1.如果 key > sortedArr[high],该值肯定找不到 * 2.如果 key < sortedArr[low],该值肯定找不到 * 3.如果low > high,逻辑不成立,不存在中间值。 */ if(key < sortedArr[low] || key > sortedArr[high] || low > high) { return false; } while(low<=high) { //满足起点<=终点就可继续,因为两者间能产生中间值 //得到中间下标值 int mid = (high+low)/2; //若key = sortedArr[mid] if(key == sortedArr[mid]) { return true; }else if(key > sortedArr[mid]) { //若key > sortedArr[mid] //缩小起点范围 low = mid + 1; }else if(key < sortedArr[mid]){ //若key < sortedArr[mid] //缩小终点范围 high = mid -1; } } //找不到返回false return false; }
main方法测试:
public static void main(String[] args) { //创建有序数组 int[] sortedArr = new int[] {1,2,3,4,5,6,7,8,9,10}; //创建查找值 int key = 10; //创建起点和终点 int low = 0; int high = sortedArr.length-1; //调用二分查找方法,返回true代表找到,否则找不到 boolean result = binarySearchByWhile(sortedArr,key,low,high); //打印结果 if(result) { System.out.println("序列中存在"+key); }else { System.out.println("序列中不存在"+key); } }
如果上面有任何不妥的地方,欢迎大家在下面留言来纠正!
觉得不错的话,动动小手点个推荐支持下作者呗!


 浙公网安备 33010602011771号
浙公网安备 33010602011771号