luoguP6187 [NOI Online 提高组]最小环 贪心 记忆化

题目让我们把序列ai重新排列，使得环上任意两个距离为ki的数字乘积之和最大。 乘法与加法不同，把四个数分为两组分别计算，再求和。 比如1 2 3 4四个数 （1 + 2）+（3 + 4） ==  (1 + 3) + (2 + 4) （1 * 2） + （3 * 4）>（1*3）+（2*4） 对于乘法而言，大的数和大的数相乘，小的数和小的数相乘，能获取更大的运算结果。

 

 

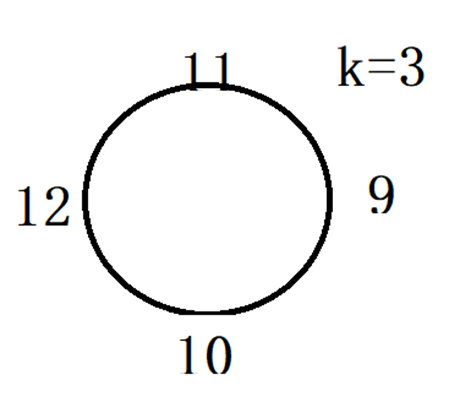
我们把这4个数，分成两部分。右上部分是11，9坐下部分是12，8这样子我们看到，最大的数，两侧是第2大和第3大的数，显然这样子，我们就不会“耽误”最大的数。

我们刚刚注意到，如果n=12，k=3。我们似乎是要填4个独立的环。我们看到，每个颜色的环，都是独立按照刚刚的方法构造的。每个环之间没有任何影响，就是第一个环填的数是[12,9]第二个环填的数是[8,5]第三个环填的数是[4,1]

那么n，k还有刚刚我们每次构造，互相独立的“环”的数量关系是什么呢？环数=gcd(n,k)环长=n/gcd(n,k)

n是不变的。比如n=9，那当k=3或者k=6时，gcd(9,3)==gcd(9,6)==3，其实构造方法是完全一样的，所以我们以环长为下标，记忆化答案，

 1 #include <cstdio>
 2 #include <algorithm>
 3 using namespace std;
 4 typedef long long ll;
 5 int n,m,k;
 6 ll ans,a[210000],f[210000];
 7 int gcd(int a,int b)
 8 {
 9     if (b == 0)
10         return a;
11     return gcd(b,a%b);
12 }
13 bool cmp(ll a,ll b)
14 {
15     return a > b;
16 }
17 int main()
18 {
19     scanf("%d%d",&n,&m);
20     for (int i = 1;i <= n;i++)
21         scanf("%lld",&a[i]);
22     sort(a + 1,a + n + 1,cmp);
23     for (int i = 1;i <= m;i++)
24     {
25         ans = 0;
26         scanf("%d",&k);
27         if (k == 0)
28         {
29             for (int j = 1;j <= n;j++)
30                 ans += a[j] * a[j];
31             printf("%lld\n",ans);
32             continue;
33         }
34         int r = n / gcd(n,k);
35         if (f[r] != 0)
36         {
37             printf("%lld\n",f[r]);
38             continue;
39         }
40         for (int c = 1;c <= n /r;c++)
41         {
42             ans += a[(c - 1) * r + 1] * a[(c - 1) * r + 2];
43             ans += a[(c - 1) * r + r - 1] * a[(c - 1) * r + r];
44             for (int j = (c - 1) * r + 1;j <= (c - 1) * r + r - 2;j++)
45                 ans += a[j] * a[j + 2]; 
46         }
47         printf("%lld\n",ans);
48         f[r] = ans; 
49     }
50     return 0;
51 }

 

posted @ 2020-03-14 23:48  IAT14  阅读(287)  评论(0)  编辑  收藏  举报