向量点乘 推导及应用

u=(u1,u2,u3) v=(v1,v2,v3)

 

dot（点乘 & 内积）

结果是一个float，表示两个向量的夹角。点积公式：u * v = u1v1+u2v2+u3v33=lul*lvl*COS(U,V)

如果点乘的结果为0，那么这两个向量互相垂直；如果结果大于0，那么这两个向量的夹角小于90度；如果结果小于0，那么这两个向量的夹角大于90度

 

例子:

 

图(a)中 向量AC投影到v

 

图(b)定义了由向量v顺时针旋转90°得到.从c向L做垂线,可以将c分解成沿v方向的部分Kv和垂直v方向的部分,其中K M是特定的常数.即:

 (1)                                                       

给定c和v,我们想得到K和M.求出这两个值后,我们可以说c到v的正交投影是Kv并且点C到直线的距离是.

求解含量个未知数的两个方程的方法是消去一个未知数,即:让等式两边都点乘v

 (2)                                                   

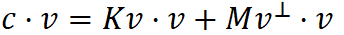
根据 如果点乘的结果为0，那么这两个向量互相垂直 得知   结果是0所以

 (3)                                                   

即:

(4)                                                    

同理:让等式(1)两边同时点乘可以得到

(5)                                                    

合并以上结果

(6)

 

 

投影应用:反射

 

 

假设 a n都是单位向量

那么a在n上的投影是-a点成n

r-a是在这一投影的基础上又加上一个也就是说r-a是沿方向n,长度为的向量.

于是