hdu 6155 - Subsequence Count

话说这题比赛时候过的好少，连题都没读TOT

先考虑dp求01串的不同子序列的个数。

dp[i][j]表示用前i个字符组成的以j为结尾的01串个数。

如果第i个字符为0，则dp[i][0] = dp[i-1][1] + dp[i-1][0] + 1，dp[i][1] = dp[i-1][1]

如果第i个字符为1，则dp[i][1] = dp[i-1][1] + dp[i-1][0] + 1，dp[i][0] = dp[i-1][0]

显然这是线性递推，我们考虑如何用矩阵表示这种递推关系。

下面分别对应加入一个字符0或1时表示递推关系的矩阵。

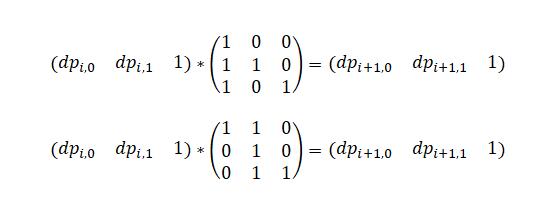
然后用线段树维护每个区间的矩阵乘积就可以解决查询操作了。

对于修改操作，我们给区间维护一个flip标记，表示该区间是否要翻转，用线段树区间更新的方法去更新flip标记就好了。

将一个区间翻转后，它对应矩阵也要发生改变，这里我们只要将矩阵的第一列与第二列交换后再将第一行与第二行交换就好了。

#include <bits/stdc++.h>
using namespace std;

const long long mod = 1e9 + 7;
const int mSize = 3;

struct Matrix
{
    long long v[mSize][mSize];
    friend Matrix operator* (const Matrix& a, const Matrix& b)
    {
        Matrix c;
        for (int i = 0; i < mSize; i++)
            for (int j = 0; j < mSize; j++)
            {
                c.v[i][j] = 0;
                for (int k = 0; k < mSize; k++)
                    c.v[i][j] += a.v[i][k] * b.v[k][j] % mod;
                c.v[i][j] %= mod;
            }
        return c;
    }
};

const Matrix m[2] = {{1, 0, 0, 1, 1, 0, 1, 0, 1}, {1, 1, 0, 0, 1, 0, 0, 1, 1}};

Matrix data[100005 << 2];
bool flip[100005 << 2];
char s[100005];

void seq_build(int o, int l, int r)
{
    if (l == r)
        data[o] = m[s[l] - '0'];
    else
    {
        int mid = (l + r) >> 1;
        seq_build(o << 1, l, mid);
        seq_build(o << 1 | 1, mid + 1, r);
        data[o] = data[o << 1] * data[o << 1 | 1];
    }
    flip[o] = false;
}

void doFlip(Matrix& mat)
{
    swap(mat.v[0][0], mat.v[0][1]);
    swap(mat.v[1][0], mat.v[1][1]);
    swap(mat.v[2][0], mat.v[2][1]);
    swap(mat.v[0][0], mat.v[1][0]);
    swap(mat.v[0][1], mat.v[1][1]);
}

void pushdown(int o)
{
    if (flip[o])
    {
        flip[o << 1] ^= flip[o];
        flip[o << 1 | 1] ^= flip[o];
        doFlip(data[o << 1]);
        doFlip(data[o << 1 | 1]);
        flip[o] = false;
    }
}

Matrix seq_query(int o, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr)
        return data[o];
    if (r < ql || qr < l)
        return {1, 0, 0, 0, 1, 0, 0, 0, 1};
    int mid = (l + r) >> 1;
    pushdown(o);
    return seq_query(o << 1, l, mid, ql, qr) * seq_query(o << 1 | 1, mid + 1, r, ql, qr);
}

void seq_flip(int o, int l, int r, int ql, int qr)
{
    if (ql <= l && r <= qr)
    {
        flip[o] ^= 1;
        doFlip(data[o]);
        return;
    }
    if (r < ql || qr < l)
        return;
    int mid = (l + r) >> 1;
    pushdown(o);
    seq_flip(o << 1, l, mid, ql, qr);
    seq_flip(o << 1 | 1, mid + 1, r, ql, qr);
    data[o] = data[o << 1] * data[o << 1 | 1];
}

int main()
{
    int t;
    scanf("%d", &t);
    while (t--)
    {
        int n, q;
        scanf("%d%d", &n, &q);
        scanf("%s", s + 1);
        seq_build(1, 1, n);
        while (q--)
        {
            int op, l, r;
            scanf("%d%d%d", &op, &l, &r);
            if (op == 1)
                seq_flip(1, 1, n, l, r);
            else
            {
                Matrix mat = seq_query(1, 1, n, l, r);
                printf("%I64d\n", (mat.v[2][0] + mat.v[2][1]) % mod);
            }
        }
    }
    return 0;
}

----------Update----------

抱歉很久没有看cnblogs了，这里给出一个不太严谨的关于flip部分的证明