数据结构和算法笔记

目录

1.汉诺塔问题

2.顺序查找

3.二分查找

4.冒泡排序

5.选择排序

6.插入排序

7.快速排序

8.堆排序

1.汉诺塔问题

汉诺塔问题可以分为三步(假设有n个盘子):

　　1.将n-1个盘子从a经过从移动到b

　　2.将第n个盘子从a移动到c

　　3.将n-1个盘子从b经过a移动到c

参数意义:

　　1.n:盘子的总个数

　　2.a:从哪个盘子 b:经过哪个盘子 c:到哪个盘子

def hanoi(n,a,b,c):
    if n>0:
        hanoi(n-1,a,c,b)
        print("moving from %s to %s" % (a,c))
        hanoi(n-1,b,a,c)      

2.顺序查找

参数意义:

　　1.li:列表

　　2.val:要查找的值

def linear_search(li,val):
    for ind,v in enumerate(li):
        if v == val:
            return ind
    else:
        return None

3.二分查找

二分查找需要注意以下几点:

　　1.二分查找存在候选区，当且仅当left<=right时，才会有候选区

　　2.根据left和right计算中间值mid的位置

　　3.用中间值和要查找的值做比较

　　　　1.如果要查找的值小于中间值mid，代表查找的值在左半部分，所以要将right位置移动到mid前面的位置

　　　　2.如果要查找的值大于中间值mid，代表查找的值在右半部分，所以要将left位置移动到mid后面的位置

　　　　3.如果要查找的值等于中间值mid，代表已经查找成功

参数意义:

　　1.li:列表

　　2.val:要查找的值

def binary_search(li,val):
    left = 0
    right = len(li) - 1
    while left <= right:
        mid=(left+right)//2
        if li[mid] == val:
            return mid
        elif li[mid] > val:
            right = mid - 1
        else:
            left = mid + 1
    else:
        return None

4.冒泡排序

冒泡排序需要注意的点:

　　1.冒泡排序主要强调"趟"和"每趟需要交换多少次元素"

　　2.设立标志位，减少多余的趟

参数意义:

　　1.li:列表

def bubble_sort(li):
    for i in range(len(li)-1): # 第i趟
        exchange = False
        for j in range(len(li)-i-1) # j代表箭头的位置
            if li[j] > li[j+1]:
                li[j],li[j+1] = li[j+1],li[j]
                exchange = True
            if not exchange:
                return

5.选择排序

选择排序原理:

　　一趟排序记录最小的数，放到第一个位置

　　再一趟排序记录列表无序区最小的数，放到第二个位置

关键点:

　　有序区和无序区，无序区最小数的位置

选择排序需要注意的点:

　　在选择排序每趟的过程中，做了如下几件事:

　　　　1.先记录一下最小数的位置下标

　　　　2.从最小数的下一个数开始循环，让每一个数和最小数进行比较，如果循环中的数比最小数小，那么就将循环中的数的位置小标赋值给min_loc

　　　　  直到这趟的循环全部结束，此时的min_loc值就是循环里的那些数中最小数的位置下标

　　　　3.如果现在得到的min_loc不是你在第1步记录的最小数的min_loc，说明最小数存在在循环中的那些数中，所以交换数值，将最小数交换到最前方(有序区中)

def select_sort(li):
    for i in range(len(li)-1):
        min_loc = i # 记录最小数的位置
        for j in range(i+1,len(li)):
            if li[j] < li[min_loc]: # 如果现在这个数比最小数位置的数小
                min_loc = j # 那么最小数的位置就是现在这个数的位置
        if min_loc != i: # 只要最小数的位置不是原来的那个位置
            li[i],li[min_loc] = li[min_loc],li[i]
                

6.插入排序

插入排序原理:

　　插入排序的原理类似于摸排，假如你手中有4.7.10三张牌，如果你摸到了一张牌为9，那么就把9插入到7和10中间的位置

关键点:

　　摸到的牌，手里的牌

插入排序需要注意的点:

　　1.每次循环开始，你都会摸到一张牌，暂时记录一下这张牌为tmp

　　2.j是你手里的牌的下标:如果我现在摸的牌下标为5，那么我手里牌的下标为4,3,2,1

　　　　现在让摸的牌[5]和手里的牌[4] 做比较

　　　　如果摸的牌[5]比手里的牌[4]小,那么将手里的牌右移一位，然后继续让摸的牌[5]和手里的牌[3]比较,直到摸的牌已经大于手里的牌，此时将摸到这张牌插入到j+1的位置

def insert_sort(li):
    for i in range(1,len(li)): # i代表你摸到的牌的下标
        tmp = li[i]
        j = i - 1 # j指的是你手里的牌的下标
        while j>=0 and tmp<li[j]:
            li[j+1]=li[j] # 将手里的牌右移一个位置
            j=j-1 # 手里的牌下标向左移动一位
        li[j+1] = tmp # 将摸到的牌放到j+1位置上

7.快速排序

1.快速排序思路

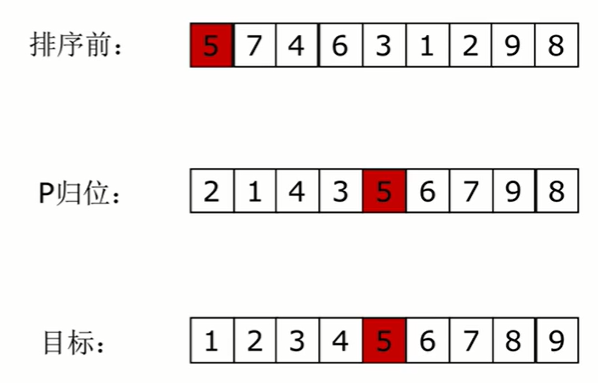
1.取一个元素p(一般是第一个元素)使元素p归位。

2.整个列表被p分成两部分,左边都比p小,右边都比p大。

3.递归完成排序。

 

2.快速排序框架代码

def quick_sort(data,left,right):
    if left < right: # 快速排序终止条件:列表中只有0个元素或者1个元素
        mid = partition(data,left,right) # 调用归位函数,得到归位元素的下标
        quick_sort(data,left,mid-1) # 对归位元素左半区列表做快速排序
        quick_sort(data,mid+1,right) # 对归位元素右半区列表做快速排序
        

3.归位函数实现代码

def partition(li,left,right):
    tmp = li[left] # 将列表中的第一个元素作为归位元素
    while left < right:
        while left < right and li[right] >= tmp: # 从右边找比tmp小的数
            right-=1 # right指向向左移动一个位置
        li[left] = li[right] # 把右边的值写到左边空位上
        while left < right and li[left] <= tmp: # 从左边找比tmp大的数
            left-=1 # left指向向右移动一个位置
        li[right] = li[left] # 把左边的值写到右边空位上
    li[left] = tmp # 把tmp归位
    return left

4.快速排序的时间复杂度

快速排序的时间复杂度是O(nlogn)

5.快速排序存在的问题

1.最坏情况

如果要排序的列表是一个完全的倒序列表(比如[9,8,7,6,5,4,3,2,1]),这个情况是快速排序的最坏情况,时间复杂度为O(n²)。

2.递归

因为python的递归存在着最大递归次数(996-1000)次,而快速排序无法保证递归次数一定是在这个范围之内的。

8.堆排序

1.堆排序前戏之二叉树

• 二叉树:度不超过2的树
• 每个节点最多有两个孩子节点
• 两个孩子节点被区分为左孩子节点和右孩子节点

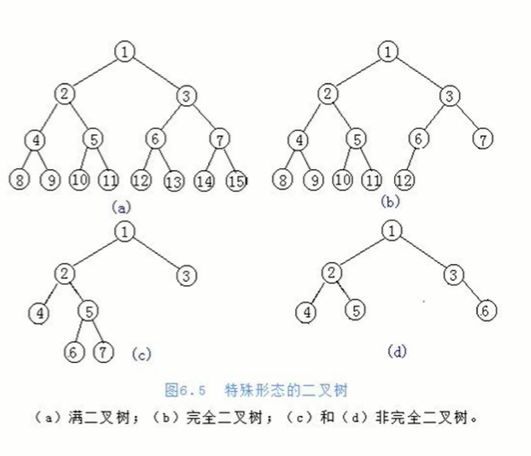
2.什么是满二叉树?

满二叉树:一个二叉树,如果每一个层的节点数都达到最大值,则这个二叉树就是满二叉树.

3.什么是完全二叉树?

完全二叉树:叶子节点只能出现在最下层和次下层,并且最下面一层的节点都集中在改成的最左边的若干位置的二叉树.

4.堆排序前戏之二叉树的存储方式

 二叉树的存储方式(表示方式):

　　1.链式存储方式

　　2.顺序存储方式 (※)

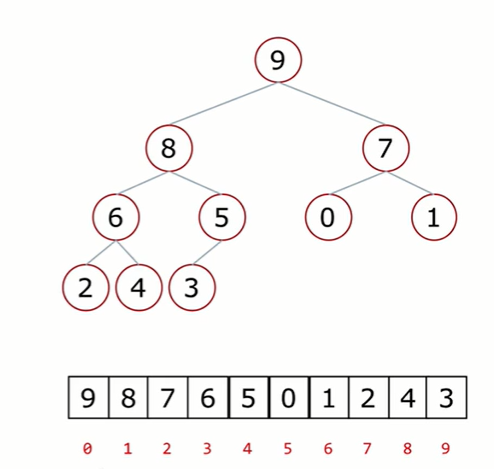
5.二叉树的顺序存储方式

父节点和左孩子节点的编号下标有什么关系?

• 0-1 1-3 2-5 3-7 4-9
• i→2i+1

父节点和右孩子节点的编号下标有什么关系?

• 0-2 1-4 2-6 3-8 4-10
• i→2i+2

 

6.什么是堆?

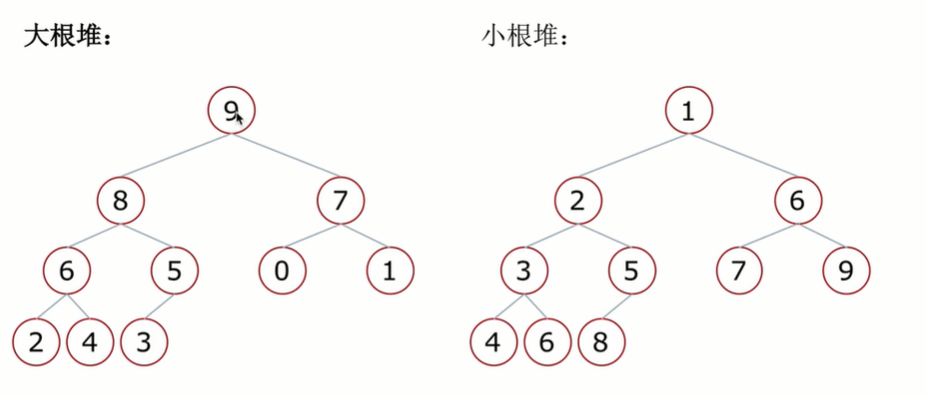
堆:一种特殊的完全二叉树结构

• 大根堆:一棵完全二叉树,满足任一节点都比其孩子节点大
• 小根堆:一棵完全二叉树,满足任一节点都比其孩子节点小

 

7.堆的向下调整

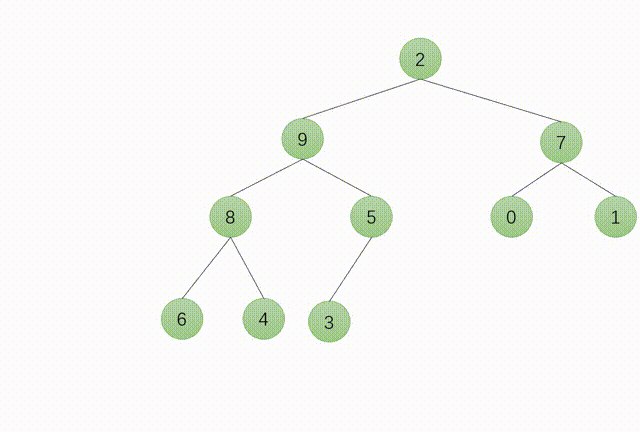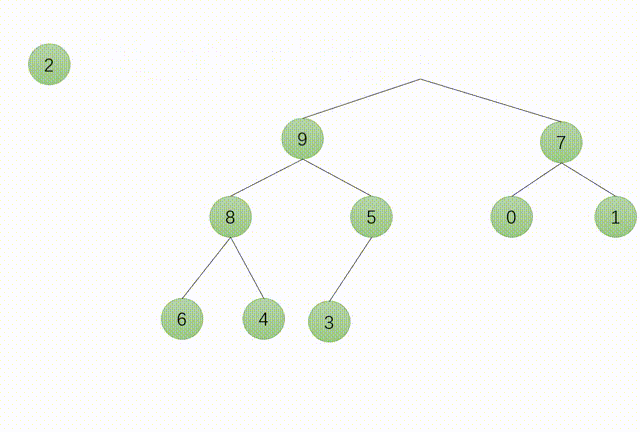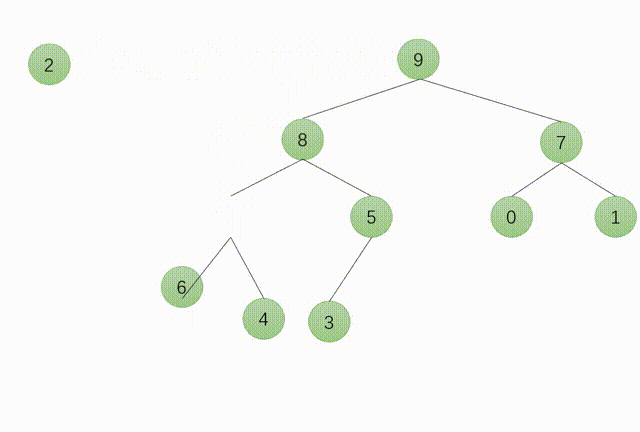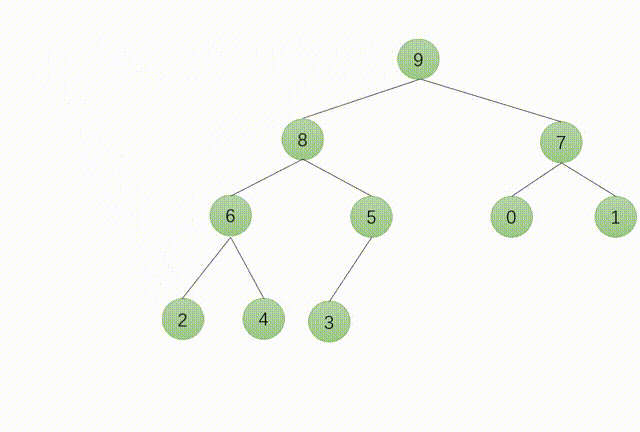
8.堆排序的实现过程

1.建立堆。

2.得到堆顶元素,为最大元素

3.去掉堆顶,将堆最后一个元素放到堆顶,此时可通过一次调整重新使堆有序

4.堆顶元素为第二大元素

5.重复步骤3,直到堆变空

9.堆的向下调整函数的实现

'''堆的向下调整函数'''
def sift(li,low,high):
    """
    li:列表
    low:堆的根节点位置
    high:堆的最后一个元素位置
    """
    i = low # i最开始的时候指向根节点
    j = 2*i+1 # j开始的时候指向左孩子节点
    tmp = li[low] # 把堆顶存起来
    while j <= high: # 只要j位置有数
        if j+1 <= high and li[j+1] > li[j]: # 如果右孩子节点存在,并且右孩子节点的值大于左孩子节点的值
            j = j+1 # j指向右孩子节点
        if li[j] > tmp:
            li[i] = li[j]
            i = j # 往下看一层
            j = 2*i+1 
        else: # tmp更大,把tmp放到i的位置上
             li[i] = tmp # 将tmp放回原位置i上(某一级领导位置上)
             break
    else:
        li[i] = tmp # 把tmp放到叶子节点上

10.堆排序函数的实现

def heap_sort(li):
    # 1.构造堆
    n = len(li)
    for i in range(n-2//2,-1,-1):
        # i表示建堆的时候调整的部分的根的下标
        sift(li,i,n-1)
    
    # 2.挨个出数
    for i in range(n-1,-1,-1): # i指向当前堆的最后一个元素
        li[0],li[i] = li[i],li[0]
        sift(li,0,i-1) # i-1是新的high 

11.堆排序的时间复杂度

堆排序的时间复杂度是O(nlogn)。