生成可执行程序的过程和数据结构
生成可执行程序的过程
1.源程序(.c) ------ 2.编译(编译包括两个阶段:预编译和正式编译)------ 3.得到目标程序(.obj)------ 4.程序模块连接阶段(与用到的库函数或者自己写的模块进行连接) ------5.生成可执行程序(.exe)。
什么是数据结构?
数据结构就是指相互有关联的数据元素的集合。元素就是数据,元素之间的关系就是结构。
实例说明:一日三餐(早餐、午餐、晚餐)
数据:数据是需要处理的数据元素的集合,一般来说,这些数据元素,具有某个共同的特征。例如,早餐、午餐、晚餐这三个数据有一个共同的特征,即它们都是一日三餐的名称,从而构成了一日三餐的集合。
结构:结构就是元素之间的关系。在数据处理领域中,通常把两两数据元素之间的关系用前后件关系(或直接前驱与直接后继关系)来描述。例如一日三餐,早餐是午餐的前件,晚餐是午餐的后件,同样午餐也是早餐的后件,以此类推。
数据结构的分类:数据的逻辑结构和存储结构。
数据的逻辑结构:数据的逻辑结构指反映数据元素之间的逻辑关系(即前后件关系)的数据结构。
数据的存储结构:数据的存储结构又称为数据的物理结构,是数据的逻辑结构在计算机存储空间中的存放方式。
数据结构的表示
二元组表示数据结构
数据的逻辑结构的数学形式定义------数据结构是一个二元组:B = (D,R)
其中,B表示数据结构,D是数据元素的集合,R是D上关系的集合,它反映了D中各数据元素之间的前后件关系,前后件也可以用一个二元组表示。例如,一日三餐看作一个数据结构,则可表示为:
B = (D , B)
D = {早餐,午餐,晚餐}
R = {(早餐,午餐),(午餐,晚餐)}
以图的形式表示数据结构
图看起来就像下图这样:
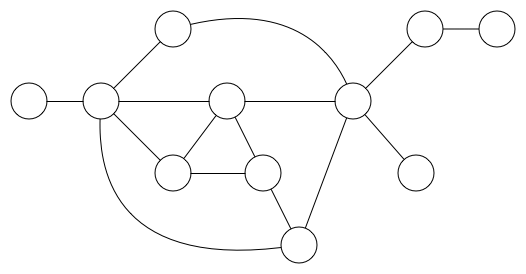
圆圈代表数据,一般称为数据节点,简称为节点。
定义:在计算机科学中,一个数据结构图就是一些圆圈或者方框包裹的数据的集合,这些圆圈或方框通过一系列连接线连接。圆圈定义为数据结构图的顶点,而这些顶点之间的连线叫边------顶点之间通过边连接。
注意:顶点有时也称为节点或者交点,边有时也称为链接。
一个图可以表示一个社交网络,每一个人就是一个顶点,互相认识的人之间通过边联系。
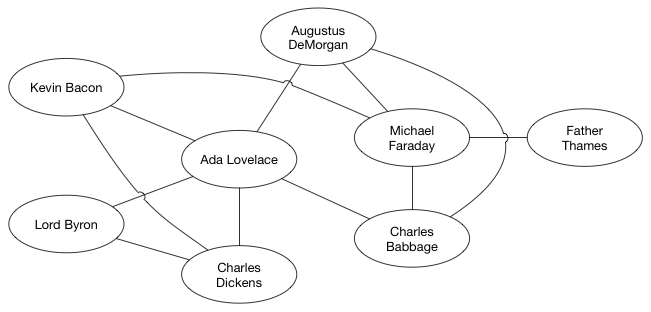
数据结构图有各种形状和大小。边可以有权重(weight),即每一条边会被分配一个正数或者负数值。考虑一个代表航线的图。各个城市就是顶点,航线就是边。那么边的权重可以是飞行时间,或者机票价格。

有了这样一张假设的航线图。从旧金山到莫斯科最便宜的路线是到纽约转机。
边可以是有方向的。在上面提到的例子中,边是没有方向的。
有方向的边的情况:
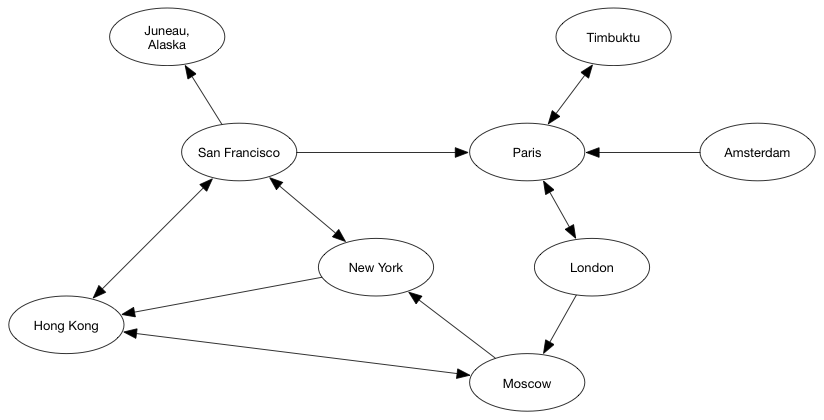
New York 到 San Francisco是双向的,而到Hong Kong是单向的。单向的就是前后件关系。
其它结构的数据结构图:
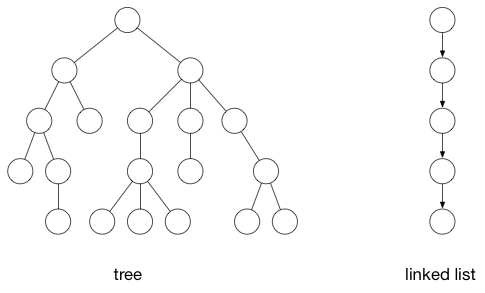
左边的是树,右边的是链表。他们都可以被当成是树,只不过是一种更简单的形式。他们都有顶点(节点)和边(连接)。
在上面的树结构数据结构图中:可以由前后件关系引出三个基本概念。
根节点:数据结构中,没有前件的节点。如上面说到的一日三餐中的早餐。
终端节点(或叶子节点):数据结构中,没有后件的节点。如晚餐。
内部节点:数据结构中,除了根节点和终端节点以外的节点。
线性结构与非线性结构:
线性结构:有且只有一个根节点,每个节点最多有一个前件和一个后件。(例如:一日三餐)
非线性结构:不满足线性结构就称为非线性结构。非线性结构主要是指树形结构和网状结构。
如果一个数据结构中没有数据元素,则称该数据结构为空的数据结构。
线性表的基本概念:
数据结构中,线性结构习惯称为线性表,线性表是最简单也是最常用的一种数据结构。
线性表的顺序存储结构:通常线性表可以采用顺序存储和链接存储两种存储结构。
采用顺序存储是表示线性表最简单的方法,具体做法是:将线性表中的元素一个接一个地存储在一片相邻的存储区域中。(顺序表)
就上面两种图(第一种是形成回路的图和第二种树和链表)比较:第一种图包含圈(cycles),即你可以从一个顶点出发,沿着一条路劲最终会回到最初的顶点。树是不包含圈的图。
另一种常见的图类型是单向图或者 DAG:
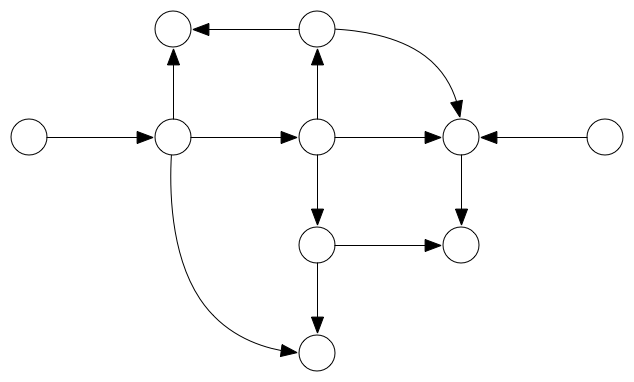
就像树一样,这个图没有任何回路(无论你从哪一个节点出发,你都无法回到最初的节点),但是这个图有有向边(通过一个箭头表示,这里的箭头不表示继承关系,而树里面是有继承关系的)。
图表示数据结构的优点:
假设你有一个编程问题可以通过顶点和边表示出来,那么你就可以将你的问题用图画出来,然后使用著名的图算法(比如广度优先搜索 或者 深度优先搜索)来找到解决方案。
例如,假设你有一系列任务需要完成,但是有的任务必须等待其他任务完成后才可以开始。你可以通过非循环有向图来建立模型:
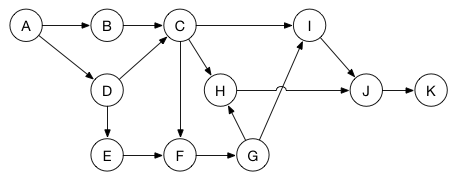
每一个顶点代表一个任务。两个任务之间的边表示目的任务必须等到源任务完成后才可以开始。比如,在任务B和任务D都完成之前,任务C不可以开始。在任务A完成之前,任务B和D都不能开始。
现在这个问题就通过图描述清楚了,你可以使用深度优先搜索算法来执行执行拓扑排序。这样就可以将所有的任务排入最优的执行顺序,保证等待任务完成的时间最小化。(这里可能的顺序之一是:A, B, D, E, C, F, G, H, I, J, K)。
