卡诺图

卡诺图

---

  卡诺图是逻辑函数的一种图形表示。

一个逻辑函数的卡诺图就是将此函数的最小项表达式中的各最小项相应地填入一个方格图内，此方格图称为卡诺图。

卡诺图的构造特点使卡诺图具有一个重要性质：可以从图形上直观地找出相邻最小项。两个相邻最小项可以合并为一个与项并消去一个变量。

---

1. 先来看一个简单的二变量卡诺图

 

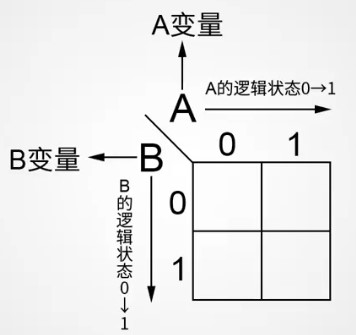
　　2. 将所有相邻为1的项圈起来

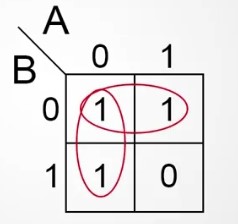
　　3. 我们先来看横向的圈，不难发现A无论为1还是0，最终结果都是1，所以该值和A无关，很明显是B的值影响了结果，当B为0时，结果为1。

　　　 我们把影响结果的参数记为B一撇（B'）。注：带一撇的都是本身为0的参数，为0的参数影响了结果，逻辑式记为：参数一撇。

　　4. 我们再来看竖直方向的圈，也不难发现B无论为1还是0，结果都是1，所以该值和B无关，很明显是A的值影响了结果，当A为0时，结果为1。

　　　 同样我们把影响结果的参数记为A一撇（A'）。

　　5.  综上两个圈，可以得出该逻辑图的函数：

　　　　Y = A'  +  B'

 

---

四变量卡诺图

 

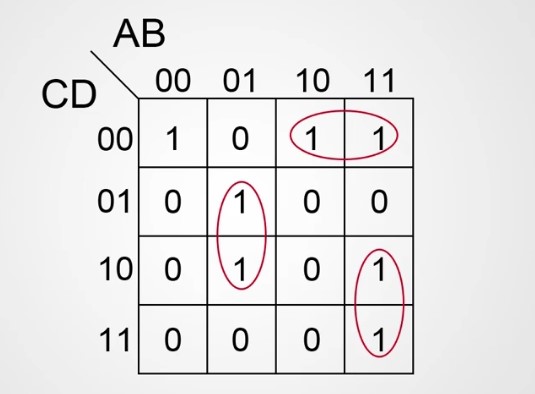
　　1. 如图将相邻的1圈起来

　　2. 然后来分析第一个横向的圈，在AB的值里面不难发现B的值对结果没有影响，而A的值只有为1时结果才为1，逻辑式为本身A;

　　　　CD的值为0时，结果才为1，逻辑式记作 C'D'，两个方向一组合（与的关系），逻辑式为：AC'D'。

　　3. 再来看第一个竖直方向的圈，在CD的值里面不论C和D为1还是0，结果都是1，所以CD为无关参数;

　　　 根据图可以得出：A=0，B=1时结果才为1，A的逻辑表达式为A'，B的逻辑表达式是本身，组合逻辑式为：A'B

　　4. 看最后一个竖直的圈，分析CD可以看出D无论0还是1结果都是1，而C为1时结果才为1，有效参数C的逻辑表达式记作为：C；

　　　  而AB都为1时结果为1，有效参数AB的逻辑式为A和B，组合表达式为：ABC。

　　5. 然后图中左上角单独的一个1的逻辑表达式为：A'B'C'D'

该卡诺图的最终逻辑表达式为：　　Y = AC'D'  + A'B  +  ABC  +  A'B'C'D'

注：画圈时只能是1、2、4、8...个相邻的1画成一个圈，即2ⁿ个相邻的1画一起，不能是3个，5个，6个，7个1画成一个圈。