树形DP——小红树

题目描述

小红拿到了一棵树,每个节点被染成了红色或者蓝色。 小红定义每条边的权值为:删除这条边时，形成的两个子树的同色连通块数量之差的绝对值。小红想知道，所有边的权值之和是多少?

输入描述

第一行输入一个正整数n,代表节点的数量。第二行输入一个长度为n且仅由'R'和'B'两种字符组成的字符串。第i个字符为'R'代表号节点被染成红色，为‘B"则被染成蓝色。接下来的n-1行，每行输入两个正整数u和v,代表节点u和节点v有一条边相连。1 <= n <=200000

 

 

 输出描述

一个正整数，代表所有边的权值之和。

 

题解

本题是典型的树形DP的问题

定义数组f，f[i]表示以i为根节点的子树中有多少个同色的连通块。

 

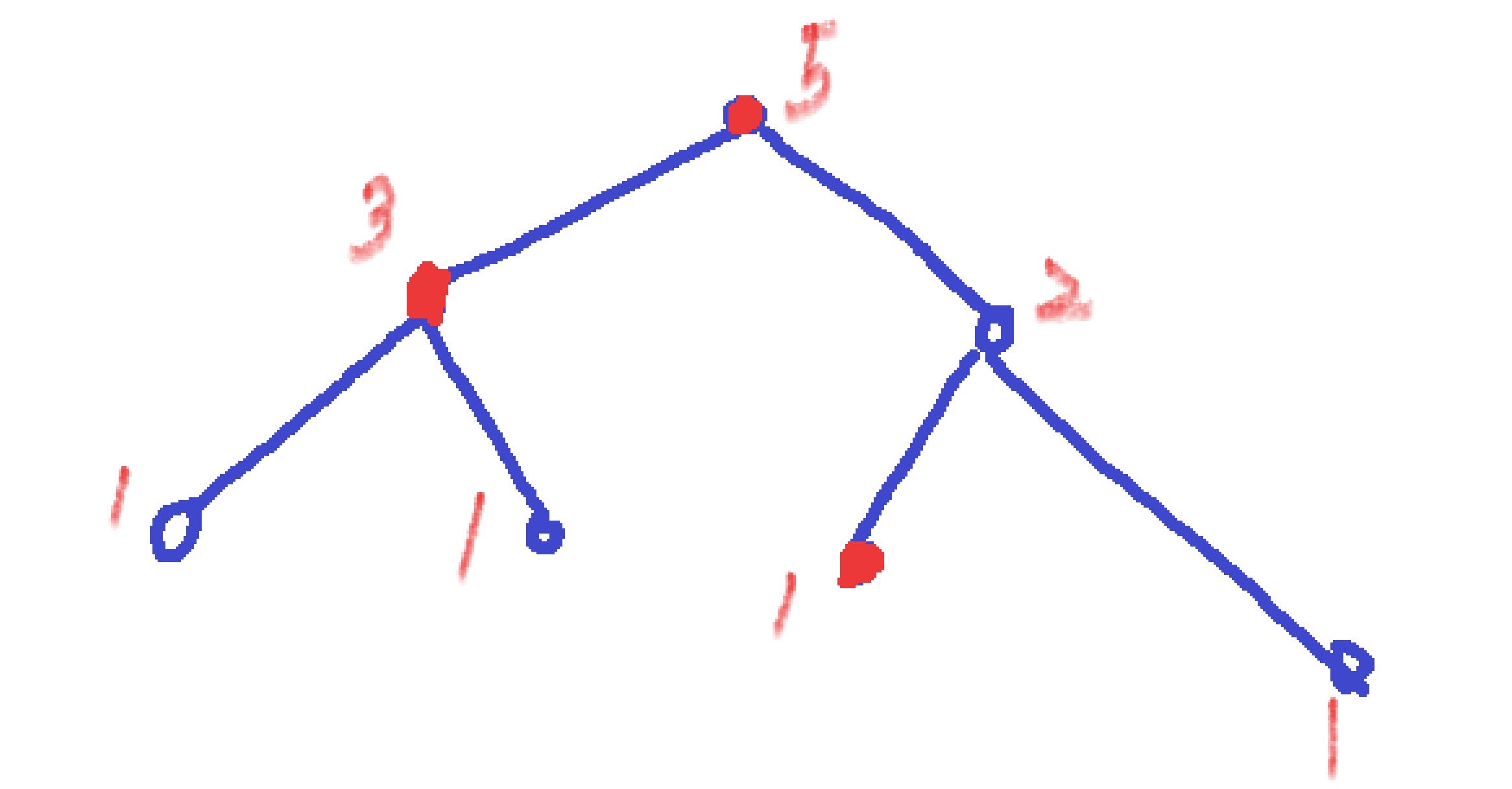
 我们可以将每个点的f值的初始值都设为1，然后递归地求每个点的f值。

如果节点x和 y的颜色不同，那么它们的同色联通块是独立的，直接累加即可：f[x] += f[y]。 如果节点 x 和 y的颜色相同，那么它们的同色联通块需要减去一个（因为它们本身算两个联通块，但是它们连接成了一个联通块），然后再累加：f[x] += f[y] - 1。

然后，我们需要对每条边计算权值。设 x - y是一条边，则有： 如果节点 x和 y的颜色相同，那么它们原本是连通的，但是现在因为断边变成了两个联通块，所以贡献为abs(f[1] - f[y] + 1 - f[y]); 如果节点 x和 y的颜色不同，那么它们原本是不连通的，现在因为连边变成了一个联通块，所以贡献为 abs(f[1] - f[y] - f[y]) 最后，我们将所有边的权值累加即可。

我们直接定义1为树的根节点，这就要dfs和计算的时候都从1开始。

 

完整代码

#include <bits/stdc++.h>
using namespace std;

const int N = 200010;
int h[N], e[N], ne[N], idx;
int f[N];
char type[N];
int res = 0;
int n;

void add(int a, int b) {
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}

void dfs(int x, int fa) {
    for(int i = h[x]; i != -1; i = ne[i]) {
        int y = e[i];
        if(y == fa) continue;
        dfs(y, x);
        if(type[x] == type[y]) {
            f[x] += f[y] - 1;
        } else {
            f[x] += f[y];
        }
    }
}

void calc(int x, int fa) {
    for(int i = h[x]; i != -1; i= ne[i]) {
        int y = e[i];
        if(y == fa) continue;
        calc(y, x);
        if(type[x] == type[y]) {
            res += abs(f[1] + 1 - f[y] - f[y]);
        } else {
            res += abs(f[1] - f[y] - f[y]);
        }
    }
}

int main() {
    ios::sync_with_stdio(0);
    cin.tie(0);
    cout.tie(0);
    cin >> n;
    memset(h, -1, sizeof h);
    for(int i = 1; i <= n; i++) {
        cin >> type[i];
    }
    for(int i = 0; i < n - 1; i++) {
        int a, b;
        cin >> a >> b;
        add(a, b);
        add(b, a);
    }
    for(int i = 1; i <= n; i++) f[i] = 1;
    dfs(1, -1);
    calc(1, -1);
    cout << res << '\n';
    return 0;
}